针对军用直升机的需求分析工作，使用XML 语言发展了作战任务场景的物理运动和逻辑发展联合推演仿真建模方法。提出了作战场景仿真模型的验证方法，采用世界各国广泛演习或推演过的直升机攻坦克战例定量结论，对仿真方法分析结果进行了定量验证。以预警直升机为例，想定一项任务场景，建立了仿真模型。发展了军用直升机设计风险的预先分层评价策略，分析了预警直升机对驱逐舰编队体系的作战效能贡献，进而面向军用直升机的设计提出了一种作战任务指标向技术指标的优化转化方法，从体系作战效能要求出发，优化得到了直升机的飞行性能相关指标。

任务场景分析是军用直升机需求分析过程中的重要一环，是装备需求的重要来源，它以军方发布的研制要求等顶层文件为依据，通过对直升机的使命任务进行更加细致的任务分解和场景想定，并以解析或仿真的方法手段将直升机放在想定的战场环境中进行分析，可以更加全面地提取出军用直升机在功能、性能和接口等方面的需求，对于工业部门深入理解军方要求、补充军方顶层文件在装备需求论述上的不足、促进直升机设计顺利高效地开展，具有重要意义。

目前，对于武器装备使命任务的研究大都聚焦于任务体系分解或对参数已知的装备进行作战效能综合评价[1-2]。但在如何根据任务指标获得合适的技术指标需求方面，目前中国还未提出具体的量化分析方法，通常仍需依赖人力决定，精准性较低、时间和经费投入较大，且容易造成过度设计。直升机的设计生产部门是将部队（客户）的使用要求转化为相应产品的纽带，因而急需解决这一问题。

本文以想定的在西北太平洋某海域J国与R 国之间发生的海战为例，通过多次仿真迭代，给出适合于该作战场景的预警直升机技术指标最低要求。

1 作战场景仿真方法

采用基于信息系统体系对抗的场景时空分析软件进行仿真，采用场景逻辑推演软件进行指控的逻辑建模与验证，开展场景联合仿真推演功能的开发，两种软件简介如下。

场景时空分析软件用于进行作战场景中作战装备的运动推演，其软件界面如图1 所示。

图1 场景时空分析软件界面

场景逻辑推演软件根据美军DoDAF 标准，采用多种视图对场景中各作战节点的逻辑状态转移和演化进行检查、仿真。本文仿真方法中采用逻辑推演软件进

行作战场景中各作战节点（装备）的逻辑功能推演。软件界面如图2 所示。

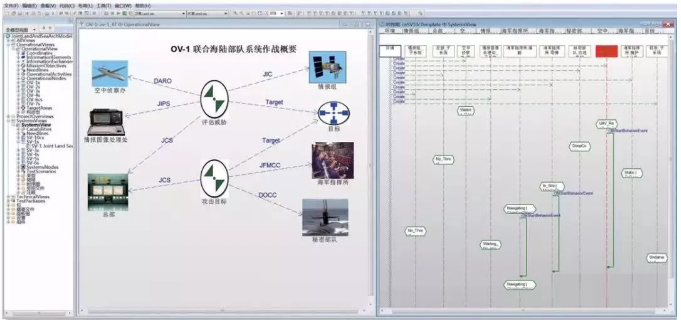
图2 逻辑推演软件界面

本文开发了网页文件如图 3 所示，该网页文件以“stk ExecuteCommand（执行命令语句）”语句控制场景时空分析软件，以“逻辑触发条件名se（t ）”语句控制场景逻辑推演软件，从而实现了两种软件之间的仿真通信，达到了装备的逻辑功能和运动数据联合演示论证的效果。

图3 运动仿真和逻辑推演两种软件的交互控制网页程序示例

2 验证方法

由于想定的作战场景和仿真结果不可能通过真实战争或演习进行试验验证，因而作战场景仿真模型的验证始终是场景分析中的难题。本文提出，通过对现代战例进行考察，从中选出与待分析的武器装备联系密切的战例，通过定量对比仿真和真实战斗的作战效能结果，可以检查软件对作战场景的仿真推演准确性。在详细作战过程未发表的情况下，可以对比多个作战结果的统计数据，以达到验证仿真模型的目的。

与敌方装甲部队的对抗是现代军用直升机最常见的作战应用[3-6]，对抗涉及到装备的攻击力、机动力和信息力等多方面的能力，相关的实战和演习数据较多——北大西洋公约组织（北约）认为，在敌方地面防空系统的支援下，直升机和敌坦克的毁伤比约为1∶12~1∶19，其他国家结论基本一致，这一量化结果适用于军用直升机作战场景软件的仿真能力定量验证。根据A 国陆军航空战斗旅和装甲旅战斗队的编制特点和战术特点，想定直升机空中突击敌方装甲集群的场景，现介绍如下。

直升机设定如下。

1）使用一个攻击直升机营，分成3 个直升机连轮番攻击敌方装甲集群，每个直升机连按“五三制”编队， 包括3 架侦察直升机和5 架攻击直升机，侦察直升机跟随在攻击直升机后方1 km 处，在保证雷达最大探测距离（约8 km）的前提下尽量保持低高度和隐蔽。每架攻击直升机上按美军反坦克任务挂载16 枚反坦克导弹和2 枚对空导弹，每架侦查直升机上挂载4 枚导弹。导弹最大射程为6000 m，直升机发射导弹的最近距离不小于3000 m。

2）直升机攻击纵深约100 km（即补给保障基地距敌方约100 km），飞行高度为15 m 并在此高度上实施攻击。本场景考虑一般作战规则，假设直升机与最近的坦克距离小于5000 m 就会向其发射导弹。

3）本文验证直升机的前飞攻击方式，这种方式中攻击直升机将在探测到第一辆坦克信息后以500 m 为半径向两侧盘旋，在反坦克导弹的离轴角内发射两枚导弹。各攻击直升机的作战任务由侦察直升机分配，编队也由此展开，侦察直升机将按攻击直升机到坦克的距离进行排序和火力分配。

在仿真中，只要直升机被2 枚导弹击中，就认为它已丧失继续战斗的能力。

5）每波次直升机中有一架发射完所有16 枚反坦克导弹，或攻击行动时间超过40 min，整个波次所有直升机应一起退出战场，返航过程中由后方侦察直升机对敌发射导弹进行掩护。

装甲集群设定如下。

1）敌方设定为A 国陆军的一个装甲旅战斗队，该队约有60 辆重型坦克（越野速度为48 km/h，最大速度为67 km/h），分为两个营，每个营配属3 部自行防空系统。在行进中令两个营组成两个梯队，第一个梯队由3个10 坦克编制队横向排列而成，后一个梯队则由3 个10 坦克编制队纵向排列而成，以形成较大的纵深，10 坦克编制队的队形如图4 所示，在其中央位置布置有一部防空系统，每部该系统上装有16 枚防空导弹。这样，整个装甲旅战斗队的坦克部队行进队形正面宽度可设置为约680 m，纵深可达到约2000 m。

图4 美军装甲旅战斗队双梯队坦克编队队形

2）坦克编队遇到空中威胁时，设定坦克和防空系统将在雷达引导下以最大速度奔向最近的直升机，一旦直升机进入自行防空系统的防空导弹射程（4000 m）， 防空系统就向其发射对空导弹，每5 枚防空导弹中会有一枚突破直升机编队的干扰而命中直升机。一旦直升机进入3000 m 的反坦克导弹防空射程，坦克也会使用反坦克导弹对其进行攻击，但发生的可能性很小（受限于地面发射与空中发射导弹的视角、高度、地面杂波不同，导弹在地面发射时射程要低于空中发射）。

3）每辆坦克装备有激光预警器和红外干扰、烟雾干扰装置，只要直升机攻击坦克的导弹飞行时间在5 s 以上，就会受到干扰，使命中率降低80%。据此，仿真中设置直升机群整体每发射5 枚导弹，才能有1 枚命中目标。为避免这种处理中违背随机原则，在攻击直升机的每轮导弹齐射当中，开火顺序都会不断变化。

4）在仿真中，只要坦克被1 枚导弹击中，就认为它已丧失继续战斗的能力。

直升机被全部击毁，或坦克被全部击毁，或3 个直升机连波次全部攻击完毕，即认为场景结束，进行敌我毁伤比统计。

根据上述信息，设置直升机、导弹和坦克的逻辑功能流如图5 示。

根据逻辑功能流图和数据信息，建立运动仿真和逻辑推演的联合仿真场景，如图6 所示。

图6 直升机攻击坦克场景联合仿真模型示意

仿真结果显示，由于装甲集群第一梯队目标较为密集，防空火力较强，直升机与坦克的损失比为2∶21， 略高于统计数据。但后面2 个波次的直升机攻击同时面对的防空火力就稀疏了很多，3 个波次攻击后直升机与坦克的毁伤比为4∶57，约等于1∶14.25，处于北约多次演习结论的区间范围以内，验证了软件对“探测—机动—攻击—毁伤”这一杀伤链过程模拟的准确性。

3 预警直升机作战任务场景想定

本文将以预警直升机的对海巡逻监视、对敌舰目标指示两种任务为研究对象，将之融入到舰艇编队作战体系中，进行作战过程的仿真推演，分析得到在编队周围巡逻警戒的舰载直升机的性能参数需求。

战斗背景想定为J国和R 国围绕西北太平洋上4 座岛屿的主权归属问题，在西北太平洋某海域爆发的海上冲突，其中两国均以水面驱逐舰编队出战，具体信息如下。

J 国：拥有20 艘Ko 级驱逐舰，最大航速为30 kn（1kn=1.852 km/h）。每艘军舰上有96 枚防空导弹，射程为22 km。8 枚反舰导弹，射程180 km。对海雷达探测距离为舰船对海平面的视距55 km。

R 国：拥有20 艘So 级驱逐舰，最大航速32 kn。每艘军舰上有 48 枚防空导弹，射程 25 km。8 枚反舰导弹，射程200 km。对海雷达探测距离为舰船对海平面的视距55 km。

由于R 国海军驱逐舰的防空系统落后于J 国使用的防空系统，R 国舰队增加了预警直升机巡逻以提高编队的信息侦察能力。战斗开始前经过两国的太空战， 双方均已丧失了卫星侦察能力。现假定R 国舰队从西北太平洋某军港出海面向J 国军舰最可能的来袭方向巡航。J国舰队在得知R 国舰队大致动向后，则从R 国舰队侧后向其逼近，企图在对海雷达探测距离上制造突然伏击，以弥补其反舰导弹射程上的劣势。但被R 国编队附近正在巡逻的舰载预警直升机发现，J 国方一旦侦测到R国直升机，也起飞预警直升机对R 国舰队进行探测和目标指示。战斗由此开始，如图7 所示（为了显示清楚，图中的舰船和直升机都做了放大处理）。

图7 作战场景战斗态势

R国舰队在巡航中，两架预警直升机在其附近作半圆形航迹的对海探测，圆弧半径固定为R 国军用数据链的200 km，如图8 所示。

图8 预警直升机对海巡航探测方式示意

每架直升机在空中除正常巡航外，还留有40 min 的巡航时间余量，在发现敌舰的情况下，可以原地小半径盘旋保持目标指示，将敌舰位置信息通过数据链下

传给R 国舰队，R 国舰队将立刻进行目标确认和任务分配，进入攻击阵位，发起导弹攻击。第一架直升机目标指示时间达到40 min 时，另一架直升机可直接接替其位置，因而信息探测任务的连贯性可以获得保证。

与此同时，J国军舰上的对空雷达系统也会发现R 国舰队直升机（但对空导弹射程不足，无法将其击落），全部舰队以最大速度向直升机方向前进，并放飞预警直升机。

作战过程设定以下参数和逻辑条件。

1）J 国和R 国的舰队队形为，相邻舰只的纵横向间隔均为10 km。

2）每探测到一艘J 国舰只进入导弹射程，即使用与之最为接近的一艘R 国舰上的全部反舰导弹进行攻击。每探测到多艘J国舰只进入多艘R 国舰只的射程， 即按距离进行排序和火力分配，每艘R 国舰只使用所有能攻击该舰的导弹进行攻击。J 国舰只探测到R 国舰只后以同样方式进行攻击。

3）反舰导弹和对空导弹的发射成功率为0.9，考虑到本场景中发射的导弹将数以百计，仿真中将在编队整体发射导弹数达到10 的整数倍时认为该发导弹未能成功射出。每枚发射成功的反舰导弹被对方探测到以后，对方将发射两枚防空导弹进行拦截，被拦截的导弹数达到10 的整数倍时可认为导弹突防成功。

4）每艘驱逐舰如果被2 枚导弹命中，即认为丧失战斗能力。

5）预警机的任务将在以下3 种情况下结束，然后进行如下双方毁伤比统计。

（1）R 国舰只被全部消灭。

（2）J 国舰只被全部消灭。

（3）R 国驱逐舰编队战斗后完全脱离J国舰只导弹射程。

在仿真中，主要关心预警直升机对作战体系信息力、攻击力、机动力和防御力的贡献，对于体系的保障力、生存力等方面则不作专门的考察。

该作战过程中预警直升机和驱逐舰编队的逻辑功能流图如图9 所示。

4 场景建模和仿真

下面根据上文中提供的预警直升机海上作战信息和功能流图，建立运动仿真和逻辑推演软件的联合仿真模型，如图10 所示。

图10 预警直升机海上作战联合仿真模型示意

5 预警真同体系贡献率分析方法

体系作战效能的评价指标有很多，本文选用其中最为典型的体系毁伤比，这相当于一个综合了体系攻击力、防御力、机动力和信息力在内的评价指标，以场景仿真的方式得出结果。本文将在作战体系中有/无该 型预警直升机的两种情况下，仿真分析作战场景中的体系作战效能，对比获得预警直升机在这一方面的体系贡献率。

首先，在无预警直升机预警的情况下，J 国舰队将绕至R 国舰队的侧后方，在55 km 的地平线距离上使用舰载雷达探测后发动攻击。R 国舰队受反舰导弹发射角制约，需要掉头转向以后才能攻击J 国舰队。通过作战场景联合仿真，最终R 国舰队对J国舰队的毁伤比为8∶4，如图11 所示（冒烟为被毁舰船）。

图11 无预警直升机情况下驱逐舰编队作战结果

然后，取预警直升机巡航速度为常见的150 km/h， 飞行高度为3000 m，进行作战场景联合仿真，最终R 国舰队对J国舰队的毁伤比为4∶7，如图12 所示。

图12 有预警直升机情况下驱逐舰编队作战结果

可以看出，在没有直升机早期预警的情况下，由于R 国舰队反应迟缓、失去先机，且反舰导弹射程上的优势无法发挥出来，造成了驱逐舰编队体系作战效能的下降。

从上面结果可知，以R 国和J国驱逐舰的作战毁伤比作为评价指标，预警直升机对驱逐舰编队的体系贡献率相对值为：（直升机产生的毁伤比减小量）（/（原毁伤比）=-1×(4/7-8/4)/(8/4)≈0.714。

6 基于任务场景的技术指标转化方法

每一任务场景中作战任务指标的实现，通常会涉及多个技术参数。相比于装备体系贡献率评估，从任务指标中分析提取技术参数指标是一个反问题。目前国内还未见到具体的量化方法被提出。

根据国家军用标准（GJB-6387）中对系统研制规范的要求，每一条款应仅做出一项规定，且条款内容应相对独立。系统规范在下发给不同专业部门后，在分系统、子系统的详细设计工作中，也不可能有太多的时间用于相互交流。因此，技术指标这种需求的提出不宜以多参数组合指标的方式存在，应按一定的规则、方法提出各项设计参数的最低要求，这些指标分别实现后， 其聚合作用应能使相应的任务要求获得满足。

本文基于优化设计思想，以直升机对体系作战效能的贡献率指标为约束，以降低性能参数的研制风险为优化目标。将直升机的作战任务指标转化为有利于设计的技术指标需求。因为性能参数的下降通常会对作战效能不利，所以这样的数学模型所得到的各种性能参数可作为设计指标下限，一切为降低研制风险和难度而确定的设计参数不能低于这一限制，否则就无法满足直升机的作战任务要求。

在本文想定的场景中，体系整体作战效能主要受直升机的续航时间tcruise、巡航速度Vcruise 和巡航高度Hcruise3 个参数的影响。下面首先建立研制风险的综合评价方法，根据文献，研制风险可以由技术风险度、进度风险度和费用风险度经加权确定，设计参数对这3 项风险的影响则应由相关专家评定。通过总体和飞行性能专业人员对性能参数的设计风险进行相对值评定， 然后根据其意见综合形成判断矩阵，通过乘权合并，最终建立与 3 个性能参数有关的设计风险综合评价公式。指标的分层设置如图13 所示。根据文献的统计结果，世界各国直升机的远航速度通常为 130~ 180 km/h，而远航高度通常为 2500~3000 m，本文将图13 中设计风险与这2 个参数的关系设置为二次函数的变化形式，二次函数的极小值点自变量值分别取为 150 km/h 和 2750 m。考虑到不同参数的变化跨度不同，用于风险评估的设计参数均根据其变化范围进行了无量纲化。

图13 设计风险分层评定指标

根据专业人员对各层指标进行相对风险量化评定的结果，构造判断矩阵（考察这一层指标对上一层指标的贡献，使用1~9 共9 个数，量化评估这一层不同指标之间的贡献相对值。每个矩阵元素的含义是行首元素对列首元素之比），见表1。

（1）判断矩阵A-C（从目标层指标A 向准则层指标C 的分解）。

与判断矩阵相关的参数为：特征值λmax=3.01，一致性指标CI=(λmax-3)/(3-1)=0.005，平均随机一致性指标RI经查表为 0.58。从而得到一致性比例CR=CI/RI=0.00862<0.1，根据分层评价理论，本矩阵的评价结果具有满意的一致性。

（2）判断矩阵C1-P（从目标层指标C1 向准则层指标P 的分解），见表2。

表 2 中，λmax=3.0092，CI=(λmax=- 3)/(3- 1)=0.0046，RI查表为 0.58，一致性比例

CR=CI/RI=0.00793<0.1，说明评价结果具有满意的一致性。

（3）判断矩阵C2-P（从目标层指标C2 向准则层指标P 的分解），见表3。

表 3 中，λmax=3.00，CI=(λmax-3)/(3-1)=0.0，RI 查表为0.58，一致性比例

CR=CI/RI=0.0<0.1，说明评价结果具有满意的一致性。

（4）判断矩阵C3-P（从目标层指标C3 向准则层指标P 的分解），见表4。

表4 中，λmax=3.0026，CI=(λmax-3)/(3-1)=0.0013，RI 查表为 0.58，一致性比例CR=CI/RI=0.00224<0.1，说明评价结果具有满意的一致性。

根据上述表1~表4，按照表5 进行层次合并，得到被评定参数层P 的总权值。

综上，与场景作战效能相关的直升机研制风险综合评价为（式1）

在式（1）的基础上，就可建立形如式（2）的优化数学模型，进行指标参数的优化求解。为体现出R 国舰队提前使用预警直升机和反舰导弹所形成的战场优势， 建模中将J国和R 国舰队的毁伤比要求设置为大于3∶2（等价于预警直升机的体系贡献率大于0.67）。为了保证解集为凸集（将在后面说明），并降低式方程组的求解工作量，优化模型中根据世界军用直升机的现状， 对3 个设计参数均给出了约束条件

鉴于作战仿真的复杂性，这是一个非线性规划问题。首先如果能证明目标函数是一个定义在凸集上的凸函数，则搜索到的目标函数极小值或边界处的最小值就是目标函数在定义域上的唯一最小值点，现证明如下（将可行解向量记为X = [Vcruise , tcruise ,Hcruise]T ）。

因为对于式（2）中由线性和二次函数组成的 A 的表达式，必有A(αX1 + (1 - α)X2) ≤ αA(X1) + (1 - α) A(X2)(0 < α < 1) ，所以目标函数 A 是一个凸函数；另外，通常直升机性能参数越好，对体系的作战效能贡献率越高， 性能参数的可行域即可判定为凸集。但本文场景比较复杂，需要用试算确定一个初始性能参数边界，在边界以外的参数组合才是凸集。经过在较低参数下进行仿真试算得到，在Hcruise=2500 m、Vcruise=135 km/h的情况下，可以出现J 国舰队刚好位于上一架直升机探测范围边界处、没有被上一架直升机探测到，而只能被下一架直升机探测到的临界情况。此时R 国舰队还未进入J 国舰队的射程范围，仿真结果为NJ-Destroy/NR-Destroy=3/2。性能参数若高于上面的值，必可提早发现J 国舰只、提高作战效能。据此构建了式（2）中的性能参数可行域，它可构成一个凸集。

本文将采用可行方向法求解式（2）表达的非线性规划问题。首先将设计风险A 的函数记为A=A(X)，将各项约束条件经过移项后记为函数形式G=G(X)≥0，则可行方向法的优化流程可分为如下6 步。

1）选定一个初始点 X (0) = [150, 5.8, 2750]T ，经仿真验证该点满足约束条件，记迭代次数k=0，并以5%的差值变化量，使用均匀样本法选取仿真样本，进行场景仿真和结果对比，求出当地梯度向量 ?A(X(k)) 。将迭代收敛时的梯度门槛值ε 设为0.5。

2）判断X(k) 是否落在G(X)=0 当中的某一项或几项约束条件边界上。

（1）若 未 落 在 任 何 约 束 条 件 边 界 上 ，且?A(X(k) )2≤ ε ，则停止迭代，

X(k)即为最优点。

（2）若 未 落 在 任 何 项 约 束 条 件 边 界 上 ，且 ?A(X(k) )2> ε ，则 将 下 一 步 的 搜 索 方 向 取 为D(k) = -?A(X(k) )，转向第5 步。

（3）若落在一项或几项约束条件边界上，设这些边界条件的序号集为J，则进入第3 步。

3）用单纯形法求如下线性规划问题的最优解。

求解得到的D 即为最优搜索方向。

4）检验解得的η 是否满足| η | < ε，若满足，则 X(k) 即为最优解。若不满足，则进入第5 步。

5）用 Fibonacci 法求解如下一维极值问题中的未知量λk。

式中，λˉ 是满足所有约束条件的最大λ，在分析推测性能参数取值时应时刻注意满足约束条件，特别是作战效能的要求。

6）令 X(k + 1) = X(k) + λD(k) ，k=k+1，返回第2 步。

求出的最优解 X(k) 是在满足作战效能约束条件下最有利于设计的参数组合，在系统规范中各参数指标需要分别罗列的前提下， X(k) 的各成分即可独立作为各项性能参数的最低指标。

利用上述方法，根据场景模型仿真结果得到最低性能指标和作战体系毁伤比（表6）。

7 结论

1）本研究所开发的软件联合仿真方法可有效模拟作战体系的运动变化。

2）本研究的仿真方法得到了北约演习统计结果的数据验证，说明该方法对作战场景的仿真结果具有一定的可信度，可以为武器装备的技术指标论证提供数据支持。

3）面向设计提出的装备作战任务指标向技术指标转换优化方法，能综合考虑多个技术指标对任务指标的影响，并从设计风险的角度对指标要求做出平衡，可

以直接支持直升机系统的顶层设计人员提出战技指标、编写系统研制规范。 参考文献请见留言补充内容