过程控制的概念与实施过程监控的方法是2 0世纪2 0年代由美国的休哈特(W. A.Shewhart)提出。二战后期，美国开始将休哈特方法在军工部门推行。战后，美国成为当时工业强大的国家，除了国内的竞争，没有外来竞争力量迫使美国公司改变传统方法。由于美国国内各公司都采用相似的生产方式，竞争性不够强，于是过程控制方法在1950年－1980年这一阶段，逐渐从美国工业中消失。

1950年，休哈特早期的一个同事戴明(W. Ed- wards Deming)博士将S P C的概念引入日本。经过1950年－1980年30年的努力，日本跃居世界质量与生产率的领先地位。美国著名质量管理专家伯格(RogerW.Berger)教授指出：日本成功的基石之一就是SPC。

SPC（Statistical Process Control）即统计过程控制。SPC应用数理统计的原理和方法对研发、生产和服务全过程进行监控和管理，从而达到改进过程与产品质量的目的。

在日本强有力的竞争下，从1980年代起，S P C在西方工业国家复兴。目前，SPC已经广泛应用于产品研发、生产和服务等过程的量化控制与管理。

一、SPC的实施步骤

1、培训SPC。培训内容主要有：SPC的重要性，正态分布等统计基本知识，质量管理七种工具，其中特别是要对控制图深入学习。

2、确定关键变量。即关键质量因素。

3、提出或改进规格标准。

4、编制控制标准，在各部门落实。

5、对过程进行统计监控。主要应用控制图对过程进行监控，若发现问题，则需对上述控制标准手册进行修订，并反馈到步骤4。

6、对过程进行诊断并采取措施解决问题。

二、SPC的控制图原理

1.控制图

控制图是对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图。图上有中心线(C L)、上控制界限( UCL ) 和下控制界限(LCL)，并有按时间顺序抽取的样本统计量数值的描点序列（参见如下控制图示例）。

2.控制图原理

假定某软件公司单位时间技术文档审核字数（千字）平均值统计数据如下：

为了找出这些数据的统计规律，我们将其作直方图。图中的直方高度与该组的频数成正比。

直方图所取得数据越多，分组越密，则直方图就越趋近一条光滑的曲线（见上图的中的曲线）。

在极限情况下得到的光滑曲线即为分布曲线，它反映了数据的统计规律。在数据特性值为连续值时，最常见的典型分布为正态分布。它的特点是中间高、两头低、左右对称并延伸至无限。正态分布是一条曲线，可用两个参数描述其特征：即平均值μ和标准差σ。

●正态曲线的特征： 曲线关于μ 对称；当x=μ时取到最大值；x离μ越远，f（x）的值越小；

●平均值（X）：把一组数据全部相加，再除以该组数据的个数。

●μ (平均值)不同：

●标准差σ（Sigma)：

总体标准差=

样本标准差 =

●标准差的意义：一组数中各单个值与总体平均数之间的平均离差，说明该组数的离散程度。通常用样本标准差近似的估计为总体标准差

●σ (标准差 )不同：

正态分布有一个结论对质量管理很有用，即无论均值μ和标准差σ取何值，产品质量特性值落在μ± 3 σ 之间的概率为9 9 . 7 3 ， 于是落在μ±3σ之外的概率为1 0 0%一99.73%= 0.27%，而超过一侧，即大于μ-3σ或小于μ+3σ的概率为0.27%/2=0.135%≈1‰，见下图。

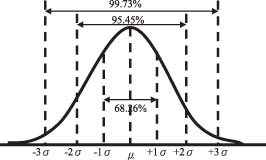
这个结论十分重要。美国休哈特就根据这一事实提出了控制图。

控制图的演变过程参见控制图的演变图。首先把正态分布曲线图（左下图）按顺时针方向转90°，由于上下的数值大小不合常规，故再把控制图的演变图上下翻转180°而成，这样就得到一张控制图（右下图）。

使用统计数据描点后的控制图：

控制图中，称X + 3σ为上控制界，记为U C L；称X为中心线，记为C L；称X-3σ为上控制界，记为L C L。这三者统称为控制线，规定中心线用实线绘制，上下控制界用虚线绘制。

3、控制图举例

为了控制研发和生产过程的质量，每隔一段时间随机抽取一个样本数据，将结果描点在控制图中，并用直线段将点子连结，以便于观察点子的变化趋势。

例如：收集到某大型软件公司的程序员未能按计划完成工作任务的5个月数据如下表：

绘制控制图如下：

由图可看出，第2、4、19点，超出控制线。

样本数据超出控制线有如下两种原因：

普通原因：是指过程在受控的状态下，出现的具有稳定的且可重复的分布过程的变差的原因。普通原因表现为一个稳系统的偶然原因。只有过程变差的普通原因存在且不改变时，过程的输出才可以预测。

特殊原因：（通常也叫可查明原因）是指造成不是始终作用于过程的变差的原因，即当它们出现时将造成（整个）过程的分布改变。只用特殊原因被查出且采取措施,否则它们将继续不可预测的影响过程的输出。

普通原因是不可避免的，但对质量的影响微小，故可把它看作背景噪声而听之任之。特殊原因则不然，它对质量的影响大，且采取措施不难消除，故在过程中特殊原因是我们注意的对象，一旦发生，就应该尽快找出，采取措施加以消除，并纳入标准化，保证它不再出现。

三、控制图的制作和使用方法

1、准备工作

●建立适合于实施的环境：排除阻碍人员公正的因素；提供相应的资源；管理者支持。

●定义过程：根据开发（生产）过程和上下使用者之间的关系，分析每个阶段的影响因素。

●确定待控制的特性：应考虑到顾客的需求、当前及潜在的问题区域、特性间的相互关系。

●确定测量系统：规定检测的人员、环境、方法、数量、频率、设备或量具；确保检测设备或量具本身的准确性和精密性。

●使不必要的变差最小：确保过程按预定的方式运行；确保输入的材料符合要求；恒定的控制设定值。

2、控制图制作（以X-R图为例）

●收集数据：选择子组大小，频率和数据；建立控制图及记录原始数据；计算每个子组的均值和极差；选择控制图的刻度；将均值和极差画到控制图上。

●计算控制限：计算平均极差及过程均值；计算控制限；在控制图上作出均值和极差控制限的控制线。

●过程控制分析：分析极差图上的数据点；识别并标注所有特殊原因（极差图）；重新计算控制限（极差图）；分析均值图上的数据点；识别并标注所有特殊原因（均值图）；重新计算控制限（均值图）；为了继续进行控制，延长控制限。

●过程能力分析：如果已经确定一个过程已处于统计控制状态，还存在过程是否有能力满足顾客需求的问题时。一般讲，控制状态稳定，说明不存在特殊原因引起的变差，而能力反映普通原因引起的变差，并且几乎总要对系统采取措施来提高能力，过程能力通过标准偏差来评价：计算过程的标准偏差；计算过程能力即按标准偏差为单位来描述的过程均值和规格界限的距离；评价过程能力。

3、分析用控制图与控制用控制图

根据不同的用途,控制图分成两类, 即分析用控制图与控制用控制图。

●分析用控制图

应用控制图时，首先将非稳态的过程调整到稳态，用分析控制图判断是否达到稳态。确定过程参数特点：分析过程是否为统计控制状态（统计稳态）；过程能力指数是否满足要求(技术稳态)。

根据统计稳态与技术稳态的是否达到可以分为如状态分类表所示的四种情况:

状态Ⅰ:统计稳态与技术稳态同时达到,这是最理想的状态。

状态Ⅱ:统计稳态未达到,技术稳态达到。

状态Ⅲ:统计稳态达到,技术稳态未达到。

状态IV:统计稳态与技术稳态均未达到。这是最不理想的状态。

显然,状态IV是最不理想的，也是不能容忍的,需要加以调整,使之逐步达到状态Ⅰ。

●控制用控制图

等过程调整到稳态后，延长控制图的控制线，作为控制用控制图。应用控制用控制图的目的是使过程保持在确定的状态。在应用控制用控制图的过程中,若过程又发生异常,则需再次使过程恢复原来的状态。

实施上述分析用控制图与控制用控制图的过程实际上就是不断进行质量改进的过程。

4、控制图应用过程中可能发生的两类错误

控制图利用抽查对生产过程进行监控,因而是十分经济的。但既是抽查就不可能没有风险。在控制图的应用过程中可能会犯以下两类错误:

●虚发警报的错误,也称第I类错误。在生产正常的情况下,纯粹出于偶然而点子出界的概率虽然很小,但总还不是绝对不可能发生的。因此,在生产正常、点子出界的场合,根据点子出界而判断生产异常就犯了虚发警报的错误或第I类错误,发生这种错误的概率通常记以α。

●漏发警报的错误,也称第Ⅱ类错误。在生产异常的情况下,产品质量的分布偏离了典型分布,但总还有一部分产品的质量特性值是在上下控制界之内的。如果抽到这样的产品进行检测并在控制图中描点,这时由于点子未出界而判断生产正常就犯了漏发警报的错误或第Ⅱ类错误,发生这种错误的概率通常记以β。

由于控制图是通过抽查来监控产品质量的,故两类错误是不可避免的。在控制图上,中心线一般是对称轴,所能变动的只是上下控制限的间距。若将间距增大,则α减小而β增大,反之,则α增大而β减小。因此,只能根据这两类错误造成的总损失最小来确定上下控制界限。