|
一. 传统的CNN加速思路
在图像识别领域,现在的CNN往往都是结构很复杂的,动辄就有几百万的网络参数,输入数据集也逐渐由低分辨图片变成高分辨率图片或是视频。在这种情况下,完成1次前向推理,计算量是非常大的,需要的时间也会很长。更不用说,对于某些应用场景(比如视频目标识别等)需要不断地发起再推理(re-inference),这就对模型的速度提出了更高的要求。客观来说,早期的CNN研究的主要关注点是提高模型的精度,在ImageNet比赛的推动下,大家通过增加网络的层数以及对网络结构进行微调(比如添加dropout、Inception结构等),使得模型能够在ImageNet数据集上取得越来越高的准确率,但这也带来了网络参数的膨胀和计算量的剧增等问题。对于这些参数量和计算量都非常大的CNN模型,往往就只能在PC端或云端进行部署,巨大的计算量和功耗使得这些网络无法用于智能手机、嵌入式设备等平台。
在这种情况下,CNN加速越来越受到研究者们的重视,大家开始考虑能不能在牺牲一定模型精度的基础上加快模型的速度,以及降低模型的功耗。最开始,CNN加速先是出现在软件层面,大家一般有两种思路:一是对现有的模型(如VGGNet、ResNet等)进行精简,删除模型中的某些部分;二是重新设计结构简单的模型(如MobileNet等),更专注于提出一些新的层结构。再后来,大家觉得CPU和GPU都不是专门为CNN设计的计算平台,在执行CNN推理时的效率实际上是不高的,于是纷纷开始设计专用于CNN的硬件加速器(即硬件层面的CNN加速)。这些硬件加速器最开始主要是在FPGA平台上实现的(即FPGA加速器),并且一般使用HLS来生成电路。到后来,为了获得更高的能效比,FPGA加速器的设计开始转向RTL级(使用Verilog或VHDL),并逐渐迁移到ASCI上(即ASCI加速器)。
二. 什么是增量推理?
但是,我们现在要讨论的CNN加速思路和传统的思路都是不同的,我们把它称为增量推理(Incremental
Inference)。一般来说,增量推理主要适用于这样一种情形:任务需要重复执行CNN推理,而且输入图片的变化是很小的(PS:视频也可以看做连续的图片)。很显然,我们上面提到的视频目标检测(Object
Recognition in Videos,ORV)就是这种类型的任务,除了ORV,基于遮挡的CNN解释(Occlusion-Based
Explanations, OBE)也属于这类任务。在这里,我们主要讨论这两种任务,其它类似的任务就不再赘述了。

图1
OBE其实就是一种解释CNN为什么能完成识别的方法,除了OBE,CNN解释还有基于梯度的CNN解释(Gradient-Based
Explanations, GBE)和基于传播的CNN解释(Propagation-Based Explanations,
PBE)等常用的方法。大家都知道CNN能对输入图片进行分类或者识别,但是很少有人知道CNN为什么能做到这一些,以及CNN是如何工作的,而CNN解释就是为了解决这些问题而提出来的。
图1给出了OBE一般的工作流程:①. 先对原本的输入图像(这里是视网膜的OCT图像)进行前向推理,得到病人的眼睛发生糖尿病性视网膜病变的预测概率,如图1(a)所示;②.
然后,在图像上放置1个小的方形遮挡片遮挡住一部分像素,再进行一次前向推理,得到1个新的预测概率,如图1(b)所示。一般而言,由于遮挡了原图的一小部分像素,预测概率会发生改变;③.
接着,通过移动遮挡片的位置,我们可以得到遮住原图不同位置的预测概率。根据预测概率的大小,对相应的遮挡片的位置进行上色(颜色越红表示概率越大,颜色越蓝表示概率越小),我们就可以得到一幅概率变化的灵敏度热力图(sensitivity
heatmap),如图1(c)所示。热力图的红色/橘色区域其实就标注出来了输入图像中对输出影响很大的区域,对OCT图像而言,这些区域往往就是病变区域。

图2
ORV就比较好理解了,它其实就是使用CNN来识别出视频中的物体。ORV一般用于安全监视、交通监控、野外动物种类追踪等应用场景,对于这些应用场景,摄像头的位置和角度是固定的,因此拍摄到的视频的背景往往都是固定不变的。在这种情况下,由于视频的每帧图像是不变的或渐变的,我们需要关注的其实只是图像中变化的部分。图2给出了一个使用跟踪摄像机来追踪野外动物的应用,可以看到,在没有动物进入摄像机的“视野”时,视频图像的画面是不变的,恒定为背景画面(即环境背景);在动物进入摄像机的“视野”后,图像发生了变化,CNN可以检测到这种变化,并使用红框圈出了变化区域,且能一直跟踪动物的移动;最后,动物离开了摄像机的“视野”,视频画面又回到了最初的背景画面。
现在,我们回到最开始的那个问题,什么是增量推理?概括来说,增量推理就是在处理输入变化不大的数据集时(比如OBE中的遮挡图片集和ORV中的固定视角视频),只对后续图片的变化区域进行再推理,而不再对整张图片进行再推理。这样,我们就可以在进行再推理时,省去大量的冗余计算,从而降低CNN推理的运算量和功耗,提高CNN推理的执行速度。在这种情况下,我们就不能再把CNN模型当做1个“黑盒子”,只关心它的输入和输出,而必须关注它的执行过程,搞清楚输入的变化是如何在CNN模型的各层之间传播的(即“拆盒子”)。
三. 增量推理的工作流程
事实上,如果我们把ORV中的变化区域视为遮挡片,那么ORV其实也可以看做一种特殊的OBE,只不过它的遮挡片(即变化区域)的大小不是固定的,可以是大小不一的长方形。因此,我们在阐述增量推理的工作流程时,为了简单,就只讨论目标任务为OBE的情况(因为目标任务为ORV的情况是类似的)。由于下文会进行公式推导,我们这里先给出本文中会用到的一些符号和其相应的意义(如表1)。
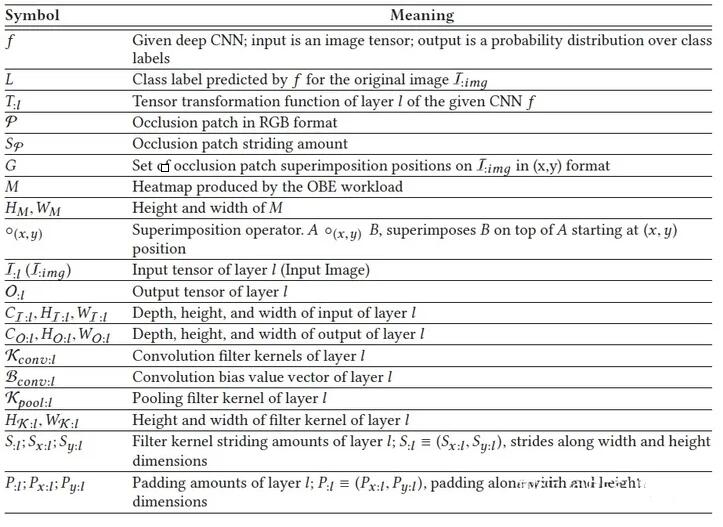
表1
假定CNN f中的某个层(或DAG)为l,其张量转换函数为T:l。OBE的输入图片为I:img,使用网络f对I:img进行处理,得到的分类标签为L。将以RGB格式给出的遮挡片记作φ,遮挡片的步长为Sφ,遮挡片的位置集合为G。将位置为(x,y)的遮挡片φ(注:(x,y)是遮挡片左上角的位置坐标)放置在原图片I:img上,那么我们就可以得到遮挡图片I'x,y:img。OBE的工作流程在上一节已经介绍过了,简单来说,就是使用CNN处理遮挡图片集,从而得到2维的输出热力图M。在这里,我们将OBE的工作流程概况为如下公式:
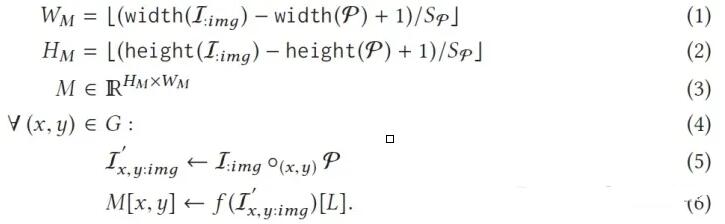
可以看到,公式(1)和公式(2)是在计算输出热力图M的宽度WM和高度HM,公式(3)则预定义了一个大小和输出热力图一样的集合M。公式(4)-(6)其实就是在进行OBE计算,公式(4)用于遍历集合G中的所有遮挡片位置(x,y),公式(5)则用于将遮挡片φ放置在原图I:img的位置(x,y)处,得到对应的遮挡图片I'x,y:img,公式(6)则是对遮挡图片I'x,y:img进行CNN推理,得到热力图M在点(x,y)处的像素值。可以看到,在遍历完遮挡片所有可能的位置后,就能得到完整的输出热力图M。值得注意的是,上面的推导都是基于CNN是在完成分类(或回归)的任务,而不适用于图像分割识别等任务。
四. CNN层的数据流
众所周知,CNN模型是由各种各样的层组成的,每个层能够将输入张量转换成另一个张量。比如,卷积层使用具有权重参数(需要在训练期间学习)的滤波器从图像中提取特征;池化层对输入特征图进行下采样,进一步筛选出重要的特征;BZ层对输入张量进行归一化操作;激活层使用非线性函数(比如ReLU)对像素单元进行激活,引入非线性;全连接层则会把层内的每个节点都与上一层的所有输出节点连接起来,把前边提取到的特征综合起来,起到“分类器”的作用。事实上,根据CNN层在进行张量变换时的空间特性,我们可以将CNN层分为3类:①.
在全局环境上进行变换的层(即全局环境粒度),比如全连接层;②. 在每个像素单元上进行变换的层(即单元粒度),比如ReLU和BZ层;③.
在局部空间环境上进行变换的层(即局部环境粒度),比如卷积层和池化层。
这种分类标准其实是比较好理解的。对于全局环境粒度的层(比如全连接层),下一层每个像素点的更新都与上一层所有的像素点有关,只要上一层有1个像素点发生变化,下一层所有像素点都必须进行更新,因此这种层是不适用于增量推理的。对于单元粒度的层(比如ReLU和BZ层),输出像素点其实就是输入像素点在某个函数上的映射,因此如果1个输入像素点改变,只会改变对应的那个输出像素点。对这种层使用增量推理是比较简单直接的,我们只需要对发生变化的输入像素点进行函数变换即可。对于局部空间环境粒度的层(比如卷积层和池化层),我们需要使用方形的滤波器逐窗口地对输入图像进行卷积运算(注:池化层可以看做1种特殊的卷积运算,其权重参数不需要进行学习),当输入像素点发生变化后,它会影响到周围几个卷积窗口。对这种层使用增量推理要困难一些,我们必须确定哪些卷积窗口受到了影响,并对相应的输出像素点进行更新。
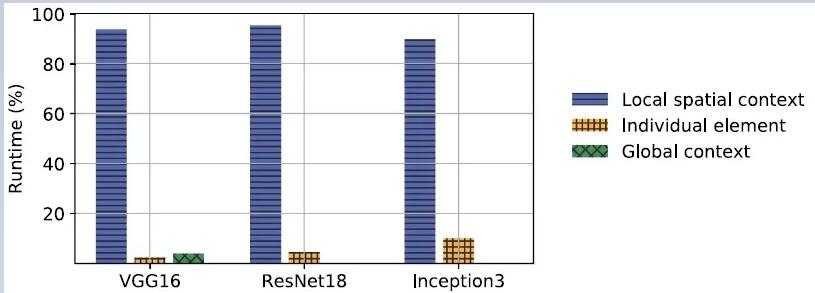
图3
图3给出了常见的CNN模型中3种类型的层的计算量的占比,可以看到,全局环境粒度的层和单元粒度的层的占比的都是比较低的,有些模型甚至没有全局环境粒度的层,因此我们选择不对全局环境粒度的层进行加速。至于单元粒度的层,由于对其进行加速是很简单的,我们也不对其进行讨论。可以看到,我们需要着重进行研究的就是局部空间粒度的层(以卷积层为主),这种层占据了CNN模型中绝大部分的计算量(超过90%)。
五. 单个层的增量推理
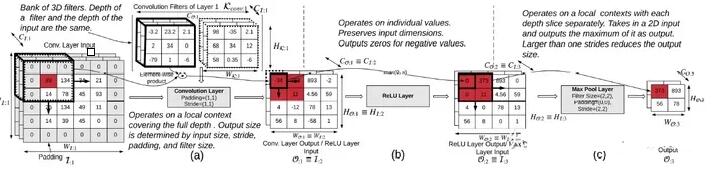
图4
图4给出了一个常见的CNN模型的关键层简单图示,其中标注的单元(黑框/红色背景)展示了1个输入像素点的变化是如何在后续层中进行传播的。图4(a)表示的是卷积层,我们使用的卷积核大小为3×3×CI:l,由于发生变化的像素点正好在输入图像的边角处,因此只会有4个卷积窗口受到影响,最后就只有4个输出像素点需要进行更新。图4(b)表示的是ReLU激活层,根据上面的分析,这1层也只会更新那4个位置的像素点,将小于0的点置为0,而大于0的点则不做变动。图4(c)表示的是最大池化层,使用的卷积核大小为2×2×1,因此会挑选出上一层那4个发生变动的像素点中最大的像素点作为输出。

图5
但是,上面的例子毕竟只是特例(注:指发生变化的像素点出现在输入图像的边角处),因此我们在下面将继续讨论在一般情况下如何确定局部环境粒度的层(主要指卷积层和池化层)的输入和输出更新片(update
patches)。在这里,由于公式推导会用到一些新的记号,我们在表2中给出了这些补充的记号和其相应的意义。如图5,假设输入遮挡片(input
patch)的位置为(xIφ:l,yIφ:l,),其高度为HIφ:l,宽度为WIφ:l。那么,使用公式(13)和(14)就能计算出输出更新片的横坐标xOφ:l和宽度WOφ:l,使用公式(15)和(16)就能计算出输入更新片的横坐标xRφ:l和宽度WRφ:l。其实这4个公式只计算了x维的参数,但计算y维的参数的公式是与之类似的,因此这里也不再赘述。可以看到,输入更新片其实就是在输入遮挡片的四周扩展(Wκ:l-1)排像素单元,输出更新片其实就是对输入更新片进行CNN推理而得到的结果。
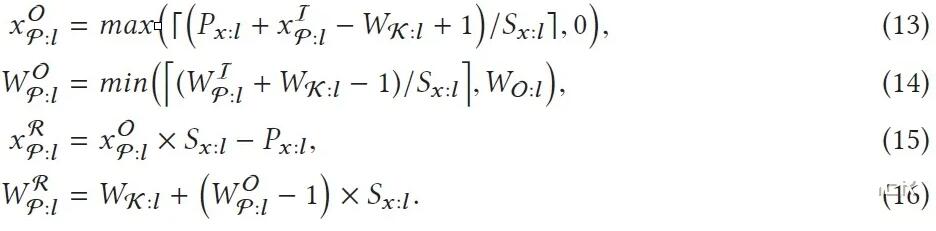
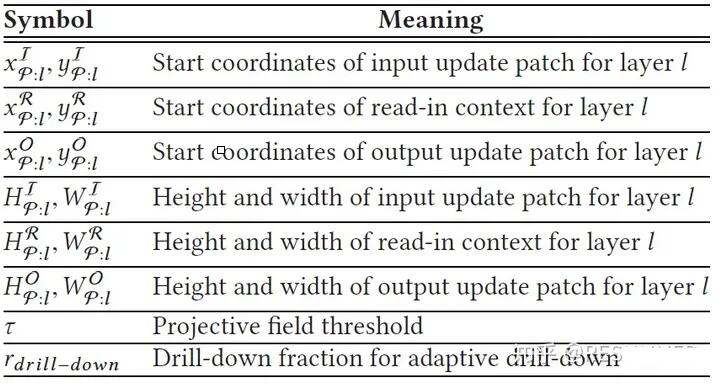
表2
在计算出输入更新片和输出更新片的位置和范围后,我们还需要计算输出更新片的像素值矩阵(如公式(17)
- (19))。可以看到,公式(17)其实就是在输入图像I:l上截取出输入更新片所在的区域,并将其记为μ;公式(18)就是在输入更新片所在的区域上放置输入遮挡片φI:l,从而得到完整的输入更新片μ;公式(19)就是使用CNN的层l对输入更新片μ进行CNN推理,从而得到输出更新片的像素值矩阵φO:l。在知道输出更新片的位置、范围和像素值矩阵后,我们就完全确定了输出更新片,也即完成了层l的增量推理。
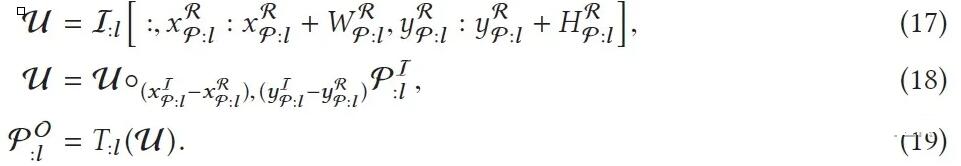
但是,上面的公式(13)-(19)也不是完美的,它们只适用于发生变化的像素点在输入图像中间的情况。对于发生变化的像素点在输入图像边缘处的情况,我们还必须特别地进行考虑。为了说明的简单,我们这里以1维情况进行说明。如图6所示,在某些特殊的情况下,会出现输出更新片的实际范围比理论计算小的情况。在图6(a)和(b)中,滤波器大小和步长是一样的,此时如果输入遮挡片的位置在1个卷积窗口内(如图6(a)),那么就会出现输出更新片的实际范围比理论计算小的情况;但如果输入遮挡片在两个卷积窗口的交界处(如图6(b)),那么输出更新片的实际范围就是和理论计算相符的。在图6(c)和(d)中,输入更新片在滤波器边界处(这里设置滤波器大小为3,步长为2),此时如果输入更新片只与两个卷积窗口相交(如图6(c)),那么就会出现输出更新片的实际范围比理论计算小的情况;而如果输入更新片与3个卷积窗口相交(如图6(d)),那么输出更新片的实际范围就是和理论计算相符的。
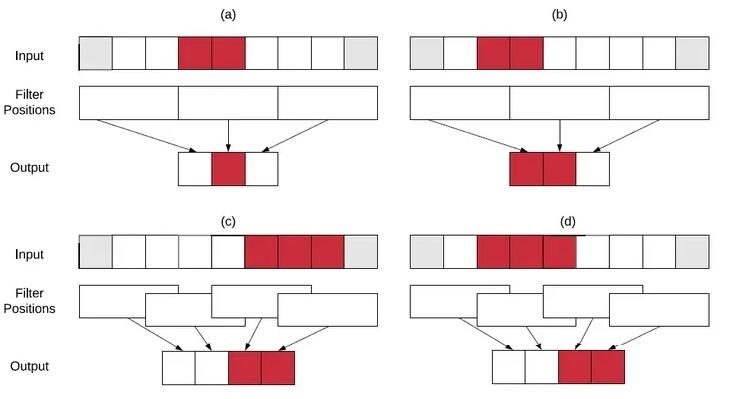
图6
那么,我们该如何处理这些特殊情况呢?我们的做法是将这些情况也当做普通情况处理,因为在这些特殊情况下,输出更新片的实际范围总是理论范围的子集。我们将特殊情况视作普通情况进行处理,虽然会额外计算一些不需要进行更新的输出像素点,从而产生冗余运算,但为了不进一步增加增量推理算法的复杂度,这点冗余运算是可以容忍的。此外,在有些情况下(特别是在进行批量增量推理时),可能会出现输出更新片越界的情况,这时我们还必须对输出更新片进行平移(如公式(20),这里也省去了y维的公式)。

六. 整个CNN的增量推理
在确定了单个层的增量推理后,我们就可以自然而然地将单个层的增量推理扩展到整个CNN中来(即整个CNN的增量推理)。对于只有1条数据通路的CNN,前1层的输出就是下1层的输入,对于这种CNN层,进行扩展是很简单的。唯一值得注意的是,如果数据流到达全局环境粒度的层,那么就会失去像素更新的局部性,这时就不能再使用增量推理了,而必须改用全局推理。但是,有些CNN是不止一条数据通路的(如某些DAG
CNN),对于这种CNN,在某些层会出现“数据汇集”的情况,这主要分为两种类型:单元级加法(element-wise
addition)和深度级串联(depth-wise concatenation)。
单元级加法其实就是将几个所有维度都相同的3维输入分张量加起来,从而得到总的输入张量,总的输入张量的维度是不会改变的;深度级串联则是将几个高度和宽度都相同的3维输入分张量串联起来,从而得到总的输入张量,总的输入张量的深度是会发生变化的。对于这两种情况,如果不止1个输入分张量有像素点发生变化,那么总的输入张量就会有多个输入遮挡片,我们该如何处理这种情况呢?
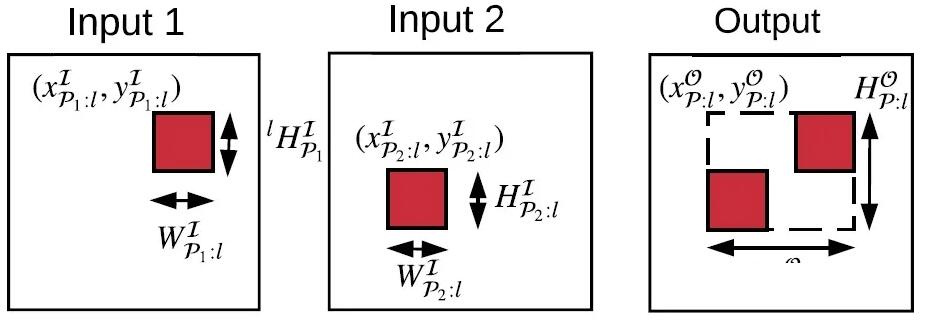
图7
图7给出了单元级加法的简单实例,这里只是两个输入分张量的相加。可以看到,输入分张量1的输入遮挡片的位置为(xIφ1:l,yIφ1:l),高度为HIφ1:l,宽度为WIφ1:l;而输入分张量2的输入遮挡片的位置为(xIφ2:l,yIφ2:l),高度为HIφ2:l,宽度为WIφ2:l。对于这种情况,我们的处理办法是:先在总的输入图像上找到一个大的方形窗口(称为“输入更新窗口”),这个方形窗口正好能将2个输入分张量的输入更新片圈起来,然后再对这个方形窗口进行增量推理。虽然这样也会计算一些不需要进行更新的输出像素点,从而引入一些计算冗余,但相比于增加算法的复杂度,这点计算冗余是可以容忍的。

公式(21)给出了计算输出更新窗口的横坐标和宽度的方法(这里也省去了y维的公式),可以看到,如果我们用1个方形窗口(称为“输入遮挡窗口”)将2个输入遮挡片圈起来,那么输入更新窗口的坐标和范围其实和这个输入遮挡窗口是一样的。很显然,这种处理方法可以用于更复杂的单元级加法或深度级串联的应用场景,我们只需要将输入更新窗口扩展为3维的输入更新块,让输入更新块能把所有发生变化的像素点都圈起来即可。
七. 批量增量推理
在使用GPU进行CNN推理时,我们经常会使用批量推理,因为这样可以利用GPU高并行度的特性,从而得到更高的输入吞吐量和更短的执行时间。但是,使用GPU进行批量增量推理是有条件限制的,并不是所有应用场景都是可用的。对于OBE和离线ORV,由于所有输入图片数据都存储在本地内存上,因此我们可以并行处理这些输入图片。在这种情况下,我们只要先对原图片先进行全局推理(full
inference),保存推理过程中的中间数据,就能在这些中间数据的基础上进行批量增量推理(Batched
Incremental Inference)。但是对于实时ORV,由于图片数据是实时获取的,一般就不能进行批量增量推理。
图8给出了对层l进行批量推理的算法流程。可以看到,步骤2-5是在计算n个输出更新片的位置和范围(批量大小为n);步骤6-10则是通过1个for循环,给出n个输入更新片的像素值矩阵(或像素值张量)μ;步骤11是对n个输入更新片进行批量增量推理;步骤12-13则用于返回n个输出更新片的参数(位置、范围和像素值矩阵)。可以看到,这个算法流程其实就是对单个层的增量推理算法进行了扩展。由于上面已经介绍了如何将单个层的批量增量推理扩展到整个CNN,为了简便,我们这里就不再重复讨论如何将单个层的批量增量推理扩展到整个CNN,毕竟这两者是非常类似的。

图8
八. 增量推理的加速比
对于CNN加速,我们最关心的指标应该就是加速比了。那么,增量推理能带来多大的加速比呢?由于CNN模型绝大部分的计算量都在卷积层(超过90%),因此我们这里近似地将CNN中卷积层的计算量作为整个CNN的计算量。假设1个卷积层的输入图片尺寸为(CI:l,
HI:l, WH:l),卷积核尺寸为(CI:l, HK:l, WK:l),输出图片尺寸为(CO:l,
HO:l, WO:l),那么如果使用全局推理(如公式(9)),这个卷积层需要进行Q:l=(CI:l
· HK:l · WK:l) (CO:l · HO:l · WO:l)次乘积累加运算(MAC)。然后,将CNN
f中的所有卷积层的计算量加起来(如公式(10)),就能得到近似的CNN总的计算量Q。

如果我们改用增量推理(如公式(11)),假设输入更新片的尺寸为(CI:l, Hφ:l, Wφ:l),那么卷积层将只需要进行Qinc:l=(CI:l
· HK:l · WK:l) (CO:l · Hφ:l · Wφ:l)次乘积累加运算。使用Q:l除以Qinc:l,就能得到单个卷积层的理论加速比为(HO:l
· WO:l)/(Hφ:l · Wφ:l)。同样地,将CNN f中所有卷积层的增量推理计算量加起来(如公式(12)),就能得到近似的CNN总的增量推理计算量Qinc,那么CNN的理论加速比就是Q/Qinc。可以看到,理论加速比Q/Qinc与很多参数有关,比如输入遮挡片的大小和位置,CNN层的参数(卷积核尺寸和步长)等。
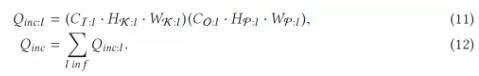
图9给出了一些常见的CNN模型随输入遮挡片大小(步长为1)的增加,理论加速比的变化曲线。可以看到,VGG-16取得了最高的加速比,而DenseNet-121的加速比则是最低的,并且绝大部分CNN的加速比都在2×到3×之间。之所以会出现这种差异,主要原因是因为不同CNN模型的结构是差异很大的。正是因为VGG-16的卷积核尺寸和步长都很小,在使用全局推理时的计算量会非常高,我们使用增量推理才取得了最高的加速比。可能一般的2×到3×的加速比看起来并不算高,但是增量推理能在不改变输出图像质量的前提下达到这个加速比,还是很难能可贵的。如果想要获得更高的加速比,我们可以在增量推理的基础上,进一步引入“近似推理”(approximate
inference)。通过牺牲一定程度的输出图像质量,可以让加速比增大至8×左右,但我们这里不再对“近似推理”作详细介绍。
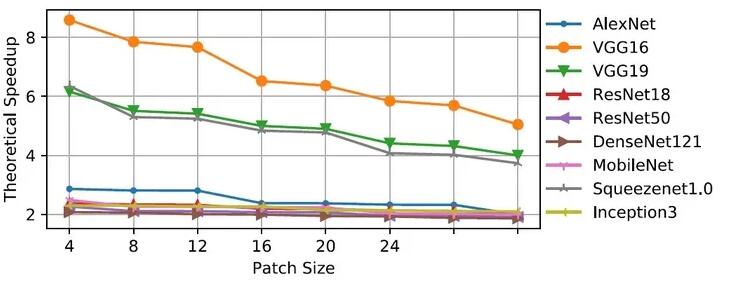
图9
为了获得增量推理的实际加速比,我们使用PyTorch对增量推理算法进行了实现,并分别在CPU和GPU上进行了测试。测试结果表明,对于非批量增量推理(即批量大小为1),实际加速比是和理论值相符的。但是,对于批量增量推理,只能在CPU上获得与理论值相符的实际加速比,批量增量推理在GPU上的执行速度甚至比全局推理还要慢。为什么会出现这种情况呢?这主要是因为GPU在执行算法1中第7行的for循环时(如图8),为了生成n个输入更新片(将用于后续的批量增量推理),必须按顺序地逐个将数据从GPU内存的一个地方复制到其它地方。这种顺序内存拷贝(sequential
memory copies)需要耗费大量时间,使得批量增量推理无法很好地利用GPU高并行度的特点,从而导致批量增量在GPU上出现执行速度慢、吞吐量小等问题。为了解决这个问题,我们通过编写1个自定义CUDA核(使用C语言)对PyTorch进行了扩展,从而让GPU在进行输入准备时,能并行地从GPU内存中拷贝数据。这其实就是1种为分片张量(注:这里指存储在不同位置的张量数据)而定制的并行for循环,通过引入这种处理机制,我们最后在GPU上也获得了与理论值相符的实际加速比。
| 