| 编辑推荐: |
本文主要介绍了深度学习神经网络基础架构相关内容。希望对你的学习有帮助。
本文来自于微信公众号算法金,由火龙果软件Linda编辑,推荐。 |
|
一、感知机
(Perceptron)
1.1 基本概念
感知机是最早的神经网络模型之一,由 Frank Rosenblatt 在 1957 年提出。它是一种二元线性分类器,用于处理二分类问题。感知机模型的基本思想是寻找一个超平面,能够将两类样本完全正确地划分开。
1.2 关键技术
感知机的关键技术包括权重和偏置。权重是用来控制输入特征对输出结果的影响程度,偏置是用来控制当所有输入特征都为零时的输出值。

感知机的工作原理可以用以下数学公式表示:
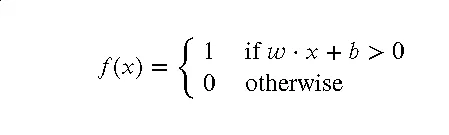
其中, w是权重, x是输入特征, b是偏置。
1.3 应用领域
感知机主要用于处理二分类问题,如垃圾邮件检测、图像识别等。
1.4 优点
感知机模型简单易懂,计算效率高,适合处理线性可分的二分类问题。
1.5 缺点
感知机模型的主要缺点是只能处理线性可分的问题,对于非线性可分的问题,感知机无法找到一个有效的超平面来正确分类。
1.6 实例分析
感知机是许多更复杂的神经网络模型的基础,如多层感知机 (MLP)。在 MLP 中,感知机被用作基本的计算单元,通过堆叠多层感知机,MLP
能够处理更复杂的问题。
1.7 手动实现
感知机的手动实现主要包括权重和偏置的初始化,以及权重和偏置的更新。在每次迭代中,感知机会根据预测结果和真实结果的差异来更新权重和偏置,直到找到一个能够正确分类所有样本的超平面。
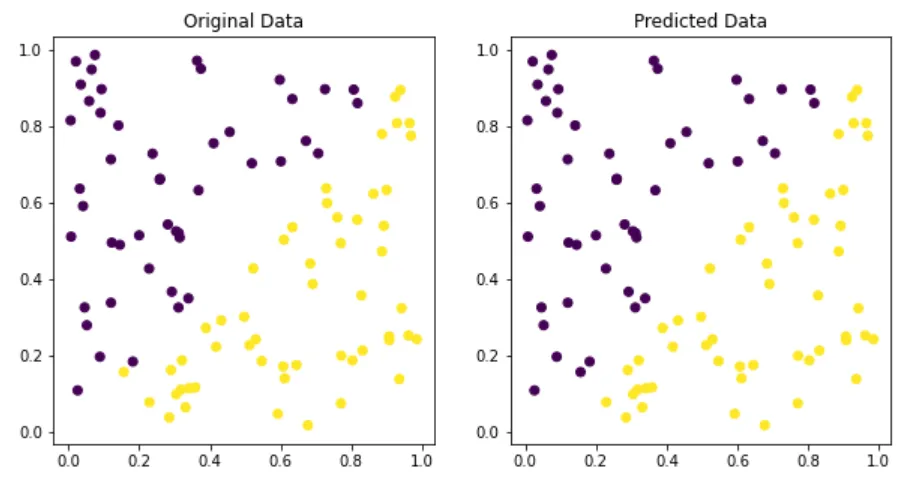
# 以下是一个简单的感知机的 Python 实现,并对比可视化原始数据和预测数据:
import numpy as np
import matplotlib.pyplot as plt
class Perceptron:
def __init__(self, learning_rate=0.01, n_iters=1000):
self.lr = learning_rate
self.n_iters = n_iters
self.activation_func = self._unit_step_func
self.weights = None
self.bias = None
def fit(self, X, y):
n_samples, n_features = X.shape
# 初始化权重和偏置
self.weights = np.zeros(n_features)
self.bias = 0
y_ = np.array([1 if i > 0 else 0 for
i in y])
for _ in range(self.n_iters):
for idx, x_i in enumerate(X):
linear_output = np.dot(x_i, self.weights)
+ self.bias
y_predicted = self.activation_func(linear_output)
# 更新权重和偏置
update = self.lr * (y_[idx] - y_predicted)
self.weights += update * x_i
self.bias += update
def predict(self, X):
linear_output = np.dot(X, self.weights) +
self.bias
y_predicted = self.activation_func(linear_output)
return y_predicted
def _unit_step_func(self, x):
return np.where(x>=0, 1, 0)
# 测试感知机
def main():
# 创建数据
np.random.seed(42)
X = np.random.rand(100, 2)
y = np.where(X[:, 0] > X[:, 1], 1, 0)
# 训练感知机
p = Perceptron(learning_rate=0.1, n_iters=100)
p.fit(X, y)
# 预测
y_pred = p.predict(X)
# 可视化结果
fig, ax = plt.subplots(1, 2, figsize=(10,
5))
ax[0].scatter(X[:, 0], X[:, 1], c=y)
ax[0].set_title('Original Data')
ax[1].scatter(X[:, 0], X[:, 1], c=y_pred)
ax[1].set_title('Predicted Data')
plt.show()
if __name__ == "__main__":
main()
|
< 
二、前馈神经网络
(Feedforward Neural Networks)
2.1 基本概念
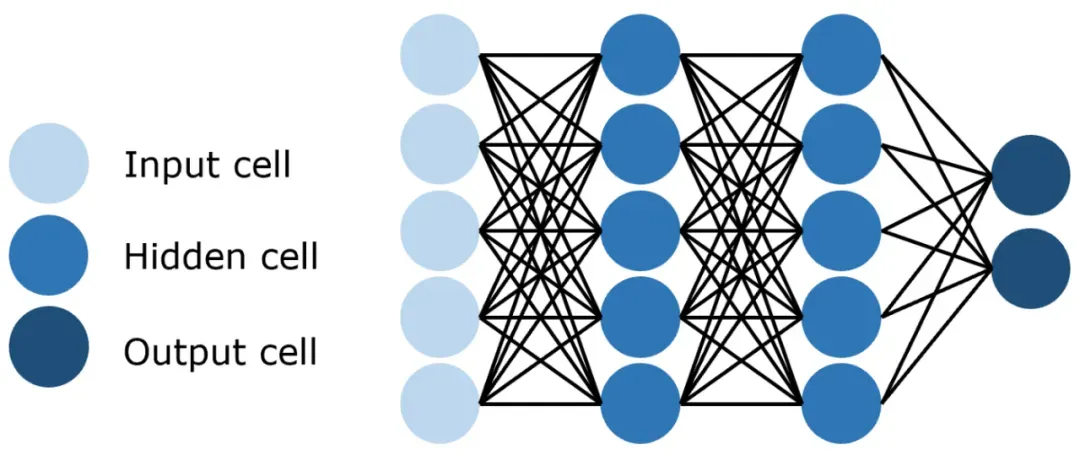
前馈神经网络是一种基本的神经网络结构,它的信息流只能向前,不能形成闭环。这种网络包括一个输入层、一个或多个隐藏层和一个输出层。每一层都由多个神经元组成,每个神经元都与下一层的所有神经元相连。
2.2 关键技术
前馈神经网络的关键技术包括权重、偏置、激活函数和反向传播算法。
权重和偏置:权重是用来控制输入特征对输出结果的影响程度,偏置是用来控制当所有输入特征都为零时的输出值。
激活函数:激活函数是用来引入非线性的,常见的激活函数有 Sigmoid、Tanh 和 ReLU 等。
反向传播算法:反向传播算法是用来更新权重和偏置的,它通过计算损失函数对权重和偏置的梯度来更新权重和偏置。
2.3 应用领域
前馈神经网络广泛应用于各种机器学习任务,包括分类、回归、聚类等。
2.4 优点
前馈神经网络的主要优点是结构简单、易于理解和实现,可以处理各种类型的数据,如数值数据、类别数据、文本数据和图像数据等。
2.5 缺点
前馈神经网络的主要缺点是可能会遇到梯度消失或梯度爆炸问题,特别是当网络层数较多时。此外,前馈神经网络需要大量的数据和计算资源来训练。
2.6 实例分析
多层感知机 (MLP) 就是一种前馈神经网络,它包含一个输入层、一个或多个隐藏层和一个输出层。MLP
可以处理更复杂的问题,如图像识别、语音识别和自然语言处理等。
2.7 手动实现
以下是一个简单的前馈神经网络的 Python 实现:
import numpy as np
class FeedforwardNeuralNetwork:
def __init__(self, n_inputs, n_hidden, n_outputs):
self.n_inputs = n_inputs
self.n_hidden = n_hidden
self.n_outputs = n_outputs
self.weights1 = np.random.rand(self.n_inputs,
self.n_hidden)
self.weights2 = np.random.rand(self.n_hidden,
self.n_outputs)
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
return x * (1 - x)
def train(self, X, y, epochs, learning_rate):
for epoch in range(epochs):
# 前向传播
hidden_layer_input = np.dot(X, self.weights1)
hidden_layer_output = self.sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output,
self.weights2)
predicted_y = self.sigmoid(output_layer_input)
# 反向传播
error = y - predicted_y
d_predicted_y = error * self.sigmoid_derivative(predicted_y)
error_hidden_layer = d_predicted_y.dot(self.weights2.T)
d_hidden_layer = error_hidden_layer * self.sigmoid_derivative(hidden_layer_output)
# 更新权重
self.weights2 += hidden_layer_output.T.dot(d_predicted_y)
* learning_rate
self.weights1 += X.T.dot(d_hidden_layer) *
learning_rate
def predict(self, X):
hidden_layer_input = np.dot(X, self.weights1)
hidden_layer_output = self.sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output,
self.weights2)
predicted_y = self.sigmoid(output_layer_input)
return predicted_y
|
这段代码首先定义了一个前馈神经网络类,然后在 `train` 方法中实现了前向传播和反向传播算法,用于训练网络。在
`predict` 方法中,使用训练好的网络进行预测。希望这个示例能帮助你理解前馈神经网络的工作原理!
2.8 实战运用
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler,
OneHotEncoder
from sklearn.metrics import accuracy_score
import numpy as np
import matplotlib.pyplot as plt
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,
y, test_size=0.3, random_state=1, stratify=y)
# 数据标准化
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# 将目标值转换为 one-hot 编码
onehot = OneHotEncoder()
y_train_onehot = onehot.fit_transform(y_train.reshape(-1,
1)).toarray()
# 训练前馈神经网络模型
fnn = FeedforwardNeuralNetwork(n_inputs=2,
n_hidden=5, n_outputs=3)
fnn.train(X_train_std, y_train_onehot, epochs=200,
learning_rate=0.01)
# 预测
y_pred = fnn.predict(X_test_std)
y_pred = np.argmax(y_pred, axis=1) # 将 one-hot
编码转换回原始类别
# 计算准确率
print('Accuracy: %.2f' % accuracy_score(y_test,
y_pred))
# 可视化结果
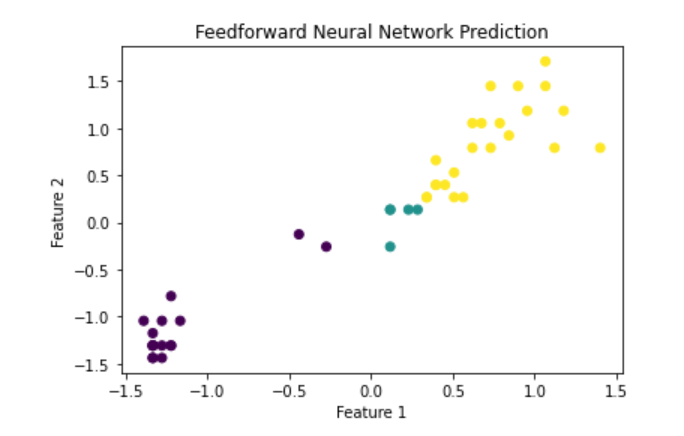
plt.figure(figsize=(6,4))
plt.scatter(X_test_std[:, 0], X_test_std[:,
1], c=y_pred)
plt.title('Feedforward Neural Network Prediction')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
|
三、多层感知机
(Multi-Layer Perceptron, MLP)
3.1 基本概念
多层感知机(MLP)是一种前馈神经网络,它包含一个输入层、一个或多个隐藏层和一个输出层。与基本的感知机模型不同,MLP
的每个神经元都使用一个非线性激活函数,如 Sigmoid 或 ReLU。这使得 MLP 能够学习并表示非线性函数,从而处理更复杂的任务。
3.2 关键技术
MLP 的关键技术包括权重、偏置、激活函数和反向传播算法。
权重和偏置:权重是用来控制输入特征对输出结果的影响程度,偏置是用来控制当所有输入特征都为零时的输出值。
激活函数:激活函数是用来引入非线性的,常见的激活函数有 Sigmoid、Tanh 和 ReLU 等。
反向传播算法:反向传播算法是用来更新权重和偏置的,它通过计算损失函数对权重和偏置的梯度来更新权重和偏置。
3.3 应用领域
MLP 广泛应用于各种机器学习任务,包括分类、回归、聚类等。
3.4 优点
MLP 的主要优点是可以处理非线性问题,适用于各种类型的数据,如数值数据、类别数据、文本数据和图像数据等。
3.5 缺点
MLP 的主要缺点是可能会遇到梯度消失或梯度爆炸问题,特别是当网络层数较多时。此外,MLP 需要大量的数据和计算资源来训练。
3.6 实例分析
MLP 是许多更复杂的神经网络模型的基础,如卷积神经网络(CNN)、循环神经网络(RNN)和深度信念网络(DBN)等。
3.7 手动实现
以下是一个简单的 MLP 的 Python 实现:
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
class MLP:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],
4)
self.weights2 = np.random.rand(4,
1)
self.y = y
self.output = np.zeros(self.y.shape)
def feedforward(self):
self.layer1 = sigmoid(np.dot(self.input,
self.weights1))
self.output = sigmoid(np.dot(self.layer1,
self.weights2))
def backprop(self):
d_weights2 = np.dot(self.layer1.T,
(2*(self.y - self.output) * sigmoid_derivative(self.output)))
d_weights1 = np.dot(self.input.T,
(np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output),
self.weights2.T) * sigmoid_derivative(self.layer1)))
self.weights1 += d_weights1
self.weights2 += d_weights2
|
这段代码首先定义了一个 MLP 类,然后在 feedforward 方法中实现了前向传播算法,用于计算网络的输出。在
backprop 方法中,实现了反向传播算法,用于更新权重。
补充:
前馈神经网络(Feedforward Neural Networks,FNN)和多层感知机(Multi-Layer
Perceptron,MLP)之间的关系非常紧密,实际上,它们可以被视为几乎相同的概念。
前馈神经网络(FNN)是一种基本的神经网络结构,它的信息流只能向前,不能形成闭环。这种网络包括一个输入层、一个或多个隐藏层和一个输出层。每一层都由多个神经元组成,每个神经元都与下一层的所有神经元相连。
多层感知机(MLP)实际上就是一种特殊的前馈神经网络。它包含一个输入层、一个或多个隐藏层和一个输出层。与基本的感知机模型不同,MLP
的每个神经元都使用一个非线性激活函数,如 Sigmoid 或 ReLU。这使得 MLP 能够学习并表示非线性函数,从而处理更复杂的任务。
所以,你可以将 MLP 视为 FNN 的一个特例,或者说,MLP 是 FNN 的一种具体实现方式。
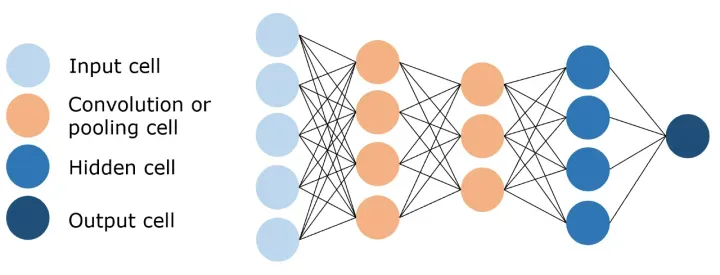
四、卷积神经网络
(Convolutional Neural Networks, CNN)
4.1 基本概念
卷积神经网络(CNN)是一种专门处理具有类似网格结构的数据的神经网络,如图像。CNN 的主要特点是它可以自动并适应地学习局部空间的输入特征。这使得
CNN 在处理图像、视频、语音和文本等数据时具有很高的效率和准确率。
4.2 关键技术
CNN 的关键技术包括卷积层、池化层和全连接层。
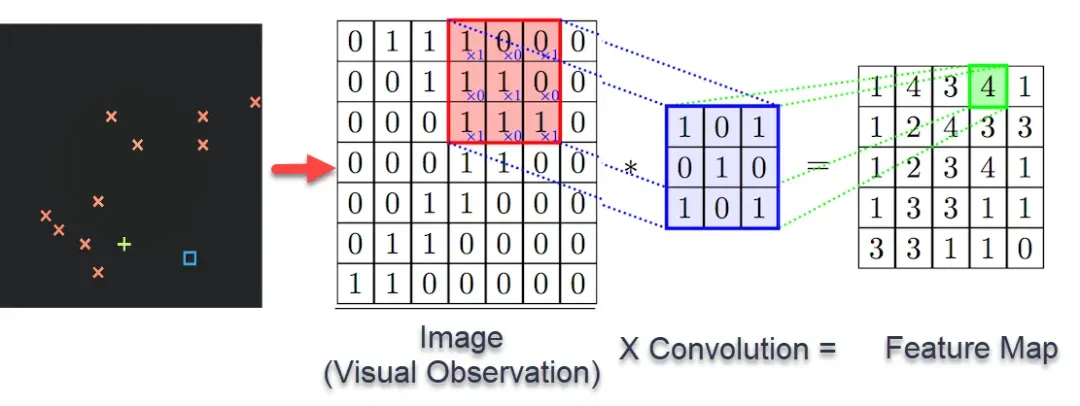
卷积层:卷积层是 CNN 的核心,它通过卷积操作来提取输入数据的特征。卷积操作可以用以下数学公式表示:
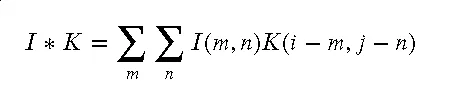
其中, i是输入数据, k是卷积核, *表示卷积操作。
池化层:池化层是用来降低数据的维度,从而减少计算量和防止过拟合。常见的池化操作包括最大池化和平均池化。
全连接层:全连接层通常位于 CNN 的最后几层,用来整合所有特征并输出最终结果。
4.3 应用领域
CNN 广泛应用于图像识别、视频分析、语音识别、自然语言处理等领域。著名的深度学习模型如 LeNet、AlexNet、VGG、ResNet
都是基于 CNN 的。
4.4 优点
CNN 的主要优点是可以自动并适应地学习局部空间的输入特征,这使得 CNN 在处理图像、视频、语音和文本等数据时具有很高的效率和准确率。
4.5 缺点
CNN 的主要缺点是需要大量的数据和计算资源来训练,而且对于超参数的选择非常敏感。
4.6 实例分析
LeNet、AlexNet、VGG 和 ResNet 是一些著名的基于 CNN 的深度学习模型。它们在图像识别等任务上取得了显著的成果。
4.7 手动实现
以下是一个简单的 CNN 的 Python 实现:
import torch
import torch.nn as nn
import torch.nn.functional
as F
from torchvision import datasets,
transforms
import matplotlib.pyplot
as plt
# 定义 CNN 类
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
self.conv1 = nn.Conv2d(1,
20, 5, 1)
self.conv2 = nn.Conv2d(20,
50, 5, 1)
self.fc1 = nn.Linear(4*4*50,
500)
self.fc2 = nn.Linear(500,
10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(-1, 4*4*50)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.log_softmax(x, dim=1)
# 加载数据
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,),
(0.3081,))
])
dataset1 = datasets.MNIST('./data',
train=True, download=True, transform=transform)
dataset2 = datasets.MNIST('./data',
train=False, transform=transform)
train_loader = torch.utils.data.DataLoader(dataset1,
batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset2,
batch_size=1000, shuffle=True)
# 初始化网络和优化器
model = SimpleCNN()
optimizer = torch.optim.SGD(model.parameters(),
lr=0.01, momentum=0.5)
# 训练网络
def train(epoch):
for batch_idx, (data, target)
in enumerate(train_loader):
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output,
target)
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{}
({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data),
len(train_loader.dataset),
100. * batch_idx / len(train_loader),
loss.item()))
# 测试网络
def test():
test_loss = 0
correct = 0
for data, target in test_loader:
output = model(data)
test_loss += F.nll_loss(output,
target, reduction='sum').item()
pred = output.data.max(1,
keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average
loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# 运行主程序
for epoch in range(1, 10):
train(epoch)
test()
|
这个 SimpleCNN 类定义了一个简单的 CNN,包括两个卷积层和两个全连接层。在 forward
方法中,定义了网络的前向传播过程。这个类可以很容易地用于训练和预测。
五、循环神经网络
(Recurrent Neural Networks, RNN)
5.1 基本概念
循环神经网络(RNN)是一种处理序列数据的神经网络,它具有记忆性,能够捕捉时间序列中的动态信息。RNN
的主要特点是网络中存在着环路,信息可以在环路中传递。
5.2 关键技术
RNN 的关键技术包括隐藏状态和循环结构。
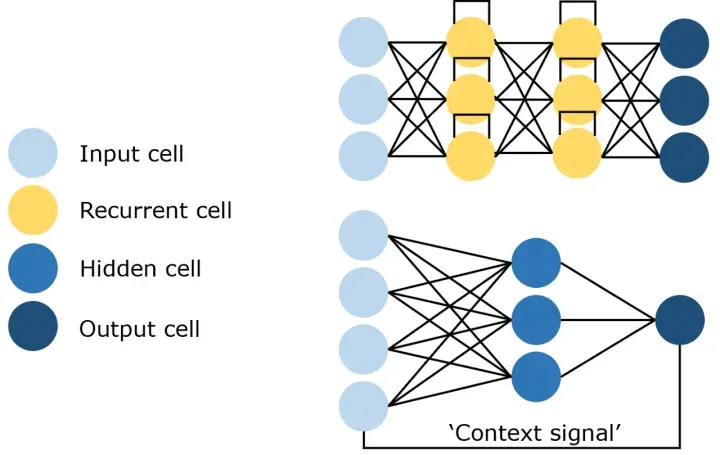
隐藏状态:在每个时间步,RNN 都会根据当前输入和前一时间步的隐藏状态来更新当前的隐藏状态。这使得
RNN 能够记住序列中的信息。
循环结构:RNN 的网络结构中存在着环路,这使得信息可以在网络中循环传播,从而捕捉序列中的动态信息。
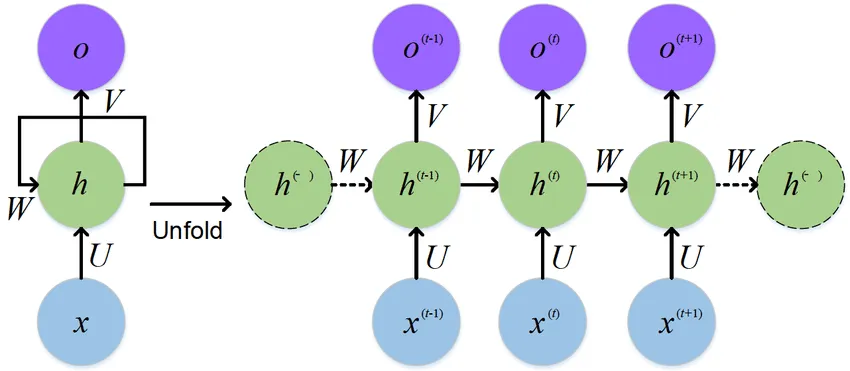
RNN 的前向传播过程可以用以下数学公式表示:
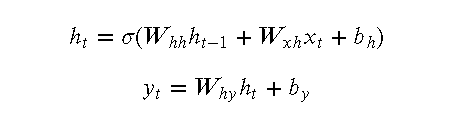

5.3 应用领域
RNN 广泛应用于自然语言处理、语音识别、时间序列预测等领域。著名的深度学习模型如 LSTM 和 GRU
都是基于 RNN 的。
5.4 优点
RNN 的主要优点是能够处理序列长度可变的数据,并且能够捕捉序列中的动态信息。
5.5 缺点
RNN 的主要缺点是训练过程可能会遇到梯度消失或梯度爆炸问题,特别是当序列长度较长时。此外,RNN
无法处理序列中的长期依赖问题。
5.6 实例分析
LSTM 和 GRU 是两种改进的 RNN 结构,它们通过引入门控机制来解决 RNN 的梯度消失和长期依赖问题。
5.7 手动实现
以下是一个简单的 RNN 的 Python 实现:
import numpy as np
class RNN:
def __init__(self, input_size,
hidden_size, output_size):
self.hidden_size = hidden_size
self.Wxh = np.random.randn(hidden_size,
input_size) * 0.01
self.Whh = np.random.randn(hidden_size,
hidden_size) * 0.01
self.Why = np.random.randn(output_size,
hidden_size) * 0.01
self.bh = np.zeros((hidden_size,
1))
self.by = np.zeros((output_size,
1))
def forward(self, inputs):
h = np.zeros((self.hidden_size,
1))
ys = []
for i in inputs:
h = np.tanh(np.dot(self.Wxh,
i) + np.dot(self.Whh, h) + self.bh)
y = np.dot(self.Why, h) +
self.by
ys.append(y)
return ys, h
def backward(self, inputs,
ys, targets):
dWxh, dWhh, dWhy = np.zeros_like(self.Wxh),
np.zeros_like(self.Whh), np.zeros_like(self.Why)
dbh, dby = np.zeros_like(self.bh),
np.zeros_like(self.by)
dhnext = np.zeros_like(ys[0])
for t in reversed(range(len(inputs))):
dy = np.copy(ys[t])
dy[targets[t]] -= 1
dWhy += np.dot(dy, ys[t].T)
dby += dy
dh = np.dot(self.Why.T, dy)
+ dhnext
dhraw = (1 - ys[t] * ys[t])
* dh
dbh += dhraw
dWxh += np.dot(dhraw, inputs[t].T)
dWhh += np.dot(dhraw, ys[t-1].T)
dhnext = np.dot(self.Whh.T,
dhraw)
return dWxh, dWhh, dWhy,
dbh, dby
|
这段代码首先定义了一个 RNN 类,然后在 forward 方法中实现了 RNN 的前向传播过程,在
backward 方法中实现了 RNN 的反向传播过程。
六、长短期记忆网络
(Long Short-Term Memory, LSTM)
6.1 基本概念
长短期记忆网络(LSTM)是一种特殊的循环神经网络(RNN),它可以学习长期依赖性。LSTM 由 Hochreiter
和 Schmidhuber 于 1997 年提出,并被许多后续的研究者改进和推广。
6.2 关键技术
LSTM 的关键技术包括遗忘门、输入门、输出门和单元状态。
遗忘门:决定了哪些信息应该被遗忘或者抛弃。
输入门:决定了哪些新的信息应该被存储在单元状态中。
输出门:基于单元状态,决定了应该输出什么样的信息。
单元状态:是 LSTM 的“记忆”部分,它在整个序列中传递信息。
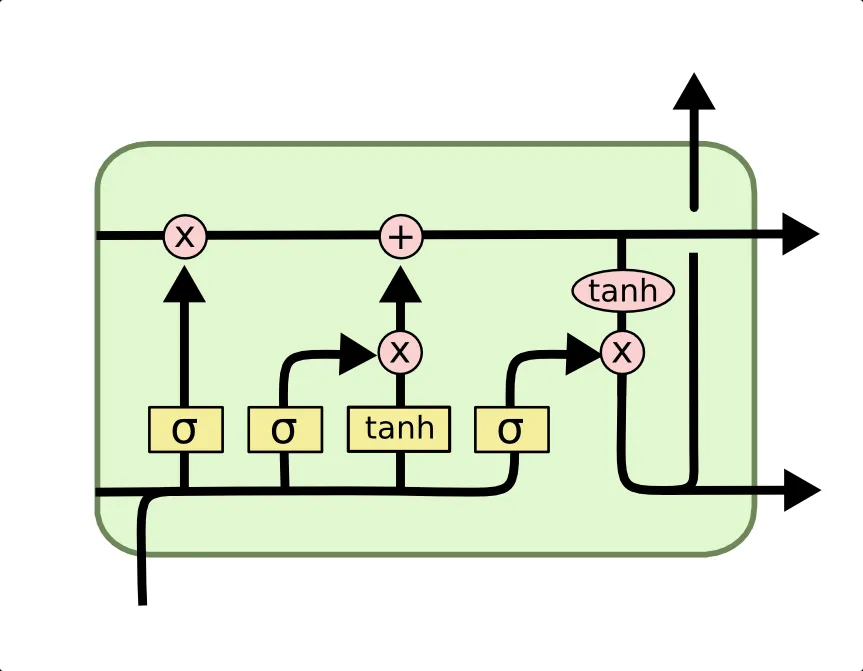
LSTM 的前向传播过程可以用以下数学公式表示:
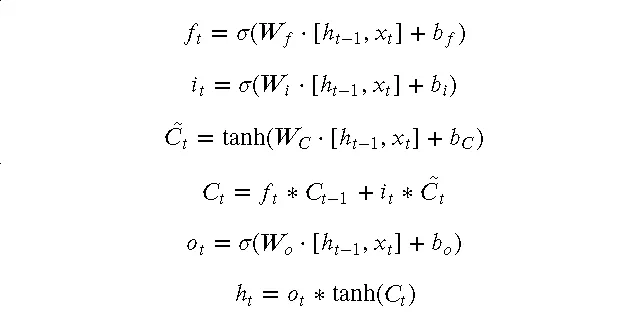

6.3 应用领域
LSTM 广泛应用于自然语言处理、语音识别、时间序列预测等领域。
6.4 优点
LSTM 的主要优点是可以有效地处理序列中的长期依赖问题,而且对于不同长度的序列,无需进行调整就可以进行处理。
6.5 缺点
LSTM 的主要缺点是计算复杂度高,需要大量的计算资源和时间来训练。
6.6 实例分析
LSTM 在许多自然语言处理任务中都取得了显著的成果,如机器翻译、情感分析和文本生成等。
6.7 手动实现
以下是一个简单的 LSTM 的 Python 实现:
import numpy as np
class LSTM:
def __init__(self, input_size,
hidden_size, output_size):
self.hidden_size = hidden_size
self.Wf = np.random.randn(hidden_size,
input_size + hidden_size)
self.Wi = np.random.randn(hidden_size,
input_size + hidden_size)
self.WC = np.random.randn(hidden_size,
input_size + hidden_size)
self.Wo = np.random.randn(hidden_size,
input_size + hidden_size)
self.Wy = np.random.randn(output_size,
hidden_size)
self.bf = np.zeros((hidden_size,
1))
self.bi = np.zeros((hidden_size,
1))
self.bC = np.zeros((hidden_size,
1))
self.bo = np.zeros((hidden_size,
1))
self.by = np.zeros((output_size,
1))
def forward(self, inputs):
h = np.zeros((self.hidden_size,
1))
C = np.zeros((self.hidden_size,
1))
ys = []
for i in inputs:
z = np.concatenate((h, i),
axis=0)
f = sigmoid(np.dot(self.Wf,
z) + self.bf)
i = sigmoid(np.dot(self.Wi,
z) + self.bi)
C_bar = np.tanh(np.dot(self.WC,
z) + self.bC)
C = f * C + i * C_bar
o = sigmoid(np.dot(self.Wo,
z) + self.bo)
h = o * np.tanh(C)
y = softmax(np.dot(self.Wy,
h) + self.by)
ys.append(y)
return ys, h, C
|
这段代码首先定义了一个 LSTM 类,然后在 forward 方法中实现了
LSTM 的前向传播过程。
七、自编码器 (Autoencoders)
7.1 基本概念
自编码器(Autoencoder)是一种无监督的神经网络模型,它试图学习输入数据的压缩表示,并能够使用这种表示重构原始输入。自编码器由两部分组成:编码器(Encoder)和解码器(Decoder)。编码器将输入数据压缩成一个隐藏表示,解码器则将隐藏表示恢复成原始数据。
7.2 关键技术
自编码器的关键技术包括编码器和解码器。
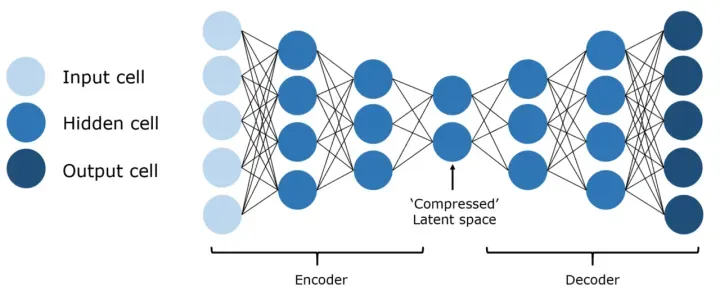
编码器:编码器是自编码器的前半部分,它将输入数据压缩成一个隐藏表示。编码器可以是任何类型的模型,但最常见的是使用全连接网络或卷积神经网络。
解码器:解码器是自编码器的后半部分,它将隐藏表示恢复成原始数据。解码器的结构通常与编码器相对称。
自编码器的训练目标是最小化重构误差,即原始输入和重构输出之间的差异。这可以用以下数学公式表示:
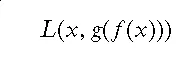
其中, x是原始输入, f(x)是编码器, g(f(x))是解码器,
l是损失函数,如均方误差。
7.3 应用领域
自编码器可以用于降维、特征学习、生成模型等多种任务。例如,它可以用于图像去噪、图像生成、文本生成等。
7.4 优点
自编码器的主要优点是能够学习输入数据的压缩表示,这使得它在处理高维数据时具有很高的效率。此外,由于自编码器是无监督的,因此它不需要标签数据就可以进行训练。
7.5 缺点
自编码器的主要缺点是可能会遇到过拟合问题,特别是当网络容量过大或训练数据过少时。此外,自编码器学习的表示可能不如一些有监督的方法(如深度神经网络)那么好。
7.6 实例分析
变分自编码器(VAE)和生成对抗网络(GAN)是两种基于自编码器的生成模型,它们在图像生成等任务上取得了显著的成果。
7.7 手动实现
以下是一个简单的自编码器的 Python 实现:
# 这段代码首先创建了一个编码器,然后创建了一个解码器,最后将编码器和解码器连接起来创建了一个自编码器。
import keras
from keras import layers
# 创建编码器
input_img = keras.Input(shape=(28,
28, 1))
x = layers.Conv2D(16, (3,
3), activation='relu', padding='same')(input_img)
x = layers.MaxPooling2D((2,
2), padding='same')(x)
x = layers.Conv2D(8, (3,
3), activation='relu', padding='same')(x)
x = layers.MaxPooling2D((2,
2), padding='same')(x)
x = layers.Conv2D(8, (3,
3), activation='relu', padding='same')(x)
encoded = layers.MaxPooling2D((2,
2), padding='same')(x)
# 创建解码器
x = layers.Conv2D(8, (3,
3), activation='relu', padding='same')(encoded)
x = layers.UpSampling2D((2,
2))(x)
x = layers.Conv2D(8, (3,
3), activation='relu', padding='same')(x)
x = layers.UpSampling2D((2,
2))(x)
x = layers.Conv2D(16, (3,
3), activation='relu')(x)
x = layers.UpSampling2D((2,
2))(x)
decoded = layers.Conv2D(1,
(3, 3), activation='sigmoid', padding='same')(x)
# 创建自编码器
autoencoder = keras.Model(input_img,
decoded)
autoencoder.compile(optimizer='adam',
loss='binary_crossentropy')
|
八、生成对抗网络
(Generative Adversarial Networks, GAN)
8.1 基本概念
生成对抗网络(GAN)是一种深度学习模型,它由两部分组成:生成器(Generator)和判别器(Discriminator)。生成器的目标是生成尽可能真实的数据,以欺骗判别器,而判别器的目标是尽可能准确地区分真实数据和生成的数据。
8.2 关键技术
GAN 的关键技术包括生成器和判别器。
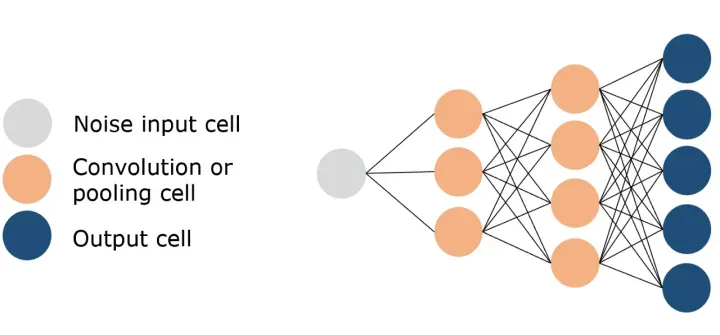
生成器:生成器是 GAN 的一部分,它的目标是生成尽可能真实的数据。生成器可以看作是一个映射函数,它将随机噪声映射到数据空间。
判别器:判别器是 GAN 的另一部分,它的目标是尽可能准确地区分真实数据和生成的数据。判别器可以看作是一个二分类器。
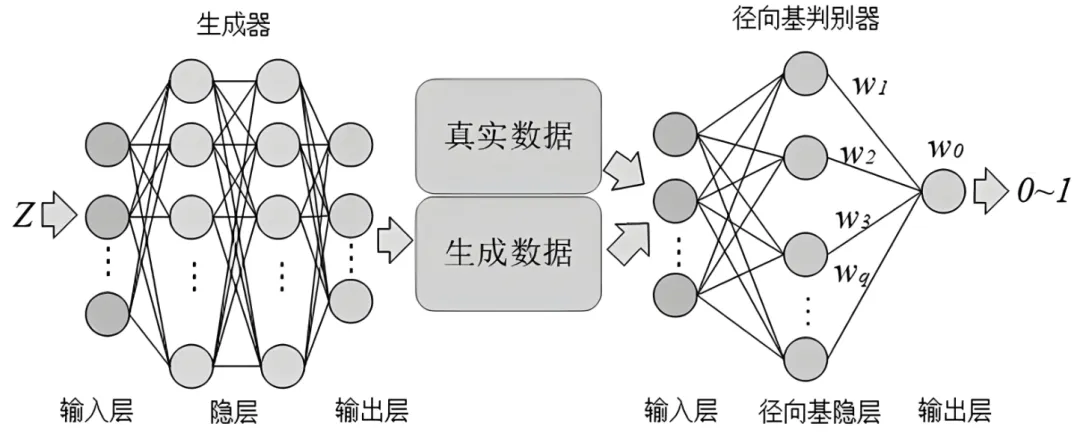
GAN 的训练过程可以看作是一个二人零和博弈,生成器和判别器互相竞争,最终达到一个纳什均衡。
8.3 应用领域
GAN 广泛应用于图像生成、图像超分辨率、图像到图像的转换等领域。
8.4 优点
GAN 的主要优点是能够生成高质量、逼真的数据。
8.5 缺点
GAN 的主要缺点是训练过程可能会遇到模式崩溃和不稳定的问题。
8.6 实例分析
DCGAN、WGAN 和 CycleGAN 是一些著名的基于 GAN 的深度学习模型,它们在图像生成等任务上取得了显著的成果。
8.7 手动实现
以下是一个简单的 GAN 的 Python 实现:
# 这段代码首先定义了一个生成器类和一个判别器类,然后在每个类的
`forward` 方法中实现了前向传播过程。
import torch
import torch.nn as nn
# 定义生成器
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.main = nn.Sequential(
nn.Linear(100, 256),
nn.ReLU(True),
nn.Linear(256, 512),
nn.ReLU(True),
nn.Linear(512, 1024),
nn.ReLU(True),
nn.Linear(1024, 784),
nn.Tanh()
)
def forward(self, input):
return self.main(input)
# 定义判别器
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.main = nn.Sequential(
nn.Linear(784, 1024),
nn.ReLU(True),
nn.Dropout(0.3),
nn.Linear(1024, 512),
nn.ReLU(True),
nn.Dropout(0.3),
nn.Linear(512, 256),
nn.ReLU(True),
nn.Dropout(0.3),
nn.Linear(256, 1),
nn.Sigmoid()
)
def forward(self, input):
return self.main(input)
|
九、强化学习网络
(Reinforcement Learning Networks)
9.1 基本概念
强化学习是一种机器学习方法,它通过让模型在环境中执行动作并根据结果获得奖励或惩罚来学习。强化学习的目标是找到一个策略,使得模型能够在长期内获得最大的累积奖励。
9.2 关键技术
强化学习的关键技术包括状态、动作、奖励和策略。

状态:状态是描述环境的信息,模型根据当前的状态来选择动作。
动作:动作是模型在环境中可以执行的操作。
奖励:奖励是模型执行动作后获得的反馈,它指导模型如何选择动作。
策略:策略是模型选择动作的方法,它可以是确定性的或者随机性的。
强化学习的过程可以用以下数学公式表示:
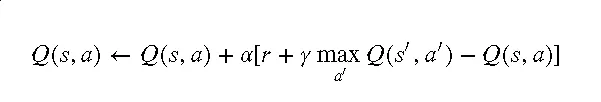
其中,Q(s,a) 是在状态 s下执行动作a 的价值,r 是奖励,
a是学习率, r是折扣因子, s′ 是新的状态,a′ 是新的动作。
9.3 应用领域
强化学习广泛应用于游戏、机器人、自动驾驶、资源管理等领域。
9.4 优点
强化学习的主要优点是能够在没有标签数据的情况下进行学习,只需要奖励信号就可以进行学习。
9.5 缺点
强化学习的主要缺点是需要大量的试错,学习过程可能会很慢。此外,强化学习可能会遇到探索和利用的平衡问题。
9.6 实例分析
Q-learning、SARSA 和 Deep Q Network (DQN) 是一些著名的强化学习算法。
9.7 手动实现
以下是一个简单的 Q-learning 的 Python 实现:
import numpy as np
class QLearning:
def __init__(self, states,
actions, alpha=0.5, gamma=0.9, epsilon=0.1):
self.states = states
self.actions = actions
self.Q = np.zeros((states,
actions))
self.alpha = alpha
self.gamma = gamma
self.epsilon = epsilon
def choose_action(self, state):
if np.random.uniform() <
self.epsilon:
action = np.random.choice(self.actions)
else:
action = np.argmax(self.Q[state,
:])
return action
def update(self, state, action,
reward, next_state):
predict = self.Q[state, action]
target = reward + self.gamma
* np.max(self.Q[next_state, :])
self.Q[state, action] = self.Q[state,
action] + self.alpha * (target - predict)
|
十、图神经网络
10.1 图神经网络原理
图神经网络(Graph Neural Network,GNN)是一种专门处理图结构数据的神经网络。其主要原理包括以下几点:
节点表示:图神经网络通过学习节点的嵌入表示来捕捉节点的特性和其在图中的位置。
邻居聚合:图神经网络通过聚合一个节点的邻居节点的信息来更新该节点的表示。这个过程可以看作是在图上进行信息传播。
权重共享:图神经网络在所有的节点和边上共享参数,这使得模型可以在不同大小和形状的图上进行推理。
可微分:图神经网络的所有操作都是可微分的,这意味着我们可以使用梯度下降等优化算法来训练模型。
10.2 图神经网络优点
处理图结构数据
图神经网络可以直接处理图结构数据,这使得它在社交网络分析、生物信息学、推荐系统等领域有着广泛的应用。
捕捉复杂依赖
通过在图上进行信息传播,图神经网络可以捕捉节点之间的复杂依赖关系。
10.3 图神经网络缺点
计算资源消耗大
由于图神经网络需要在所有的节点和边上进行计算,因此它的计算复杂度和内存消耗都较大。
难以处理动态图
虽然有一些图神经网络可以处理动态图,但是大多数图神经网络都假设图是静态的,这在一些场景下可能会限制其性能。
10.4 图神经网络的手动实现
以下是一个简单的图神经网络的 Python 实现,这里只实现了最基本的邻居聚合部分,没有包括更复杂的部分如图卷积等。由于篇幅限制,这里也没有包括可视化的部分。
import torch
import torch.nn as nn
import torch.nn.functional
as F
class GraphConvolution(nn.Module):
def __init__(self, input_dim,
output_dim):
super(GraphConvolution, self).__init__()
self.linear = nn.Linear(input_dim,
output_dim)
def forward(self, adjacency,
features):
# Apply the linear transformation
support = self.linear(features)
# Perform the convolution
output = torch.mm(adjacency,
support)
return output
|
以上是一个简单的图神经网络的实现,实际的图神经网络会更复杂,包括图卷积、图注意力网络等部分。
附一
1. 注意力机制原理
注意力机制是一种在深度学习模型中选择关键信息的方法。其主要原理包括以下几点:
权重计算:注意力机制首先会计算输入元素与目标元素之间的相关性,这通常通过计算它们的内积或者使用一个神经网络来完成。这些相关性被称为注意力权重。
加权求和:注意力机制会根据计算出的权重对输入元素进行加权求和,得到一个新的表示。这个过程可以看作是从输入元素中选择出最重要的信息。
可学习:注意力机制中用于计算权重的部分是可学习的,这意味着模型可以通过学习来改变它选择信息的方式。
2. 注意力机制优点
2.1 选择性关注
注意力机制可以让模型在处理每一个元素时都选择性地关注其他元素,这使得模型能够更好地处理复杂的输入。
2.2 可解释性
由于注意力机制的计算过程是可视化的,我们可以直观地看到模型在处理每一个元素时都关注了哪些元素,这使得模型具有很好的可解释性。
3. 注意力机制缺点
3.1 计算资源消耗大
虽然注意力机制可以帮助模型选择关键信息,但是由于它需要计算所有元素之间的相关性,因此它的计算复杂度和内存消耗都较大。
附二
1. Transformer 网络原理
Transformer 网络是一种基于自注意力机制的深度学习模型,它在自然语言处理任务中取得了显著的效果。其主要原理包括以下几点:
自注意力机制:Transformer 使用自注意力机制来捕捉输入序列中的全局依赖关系。对于每一个输入元素,自注意力机制都会计算其与其他所有元素的相关性,然后根据这些相关性对输入元素进行加权求和,得到新的表示。
位置编码:由于自注意力机制无法捕捉序列中的顺序信息,Transformer 引入了位置编码来补充这部分信息。位置编码会根据元素在序列中的位置给予其一定的编码,这样模型就能区分不同位置的元素。
多头注意力:Transformer 使用多头注意力来捕捉输入序列中的多种依赖关系。每一个注意力头都会学习到一种特定的依赖关系,多个注意力头的输出会被拼接起来,形成最终的输出。
前馈神经网络:Transformer 中的每一层都包含一个前馈神经网络,用于对注意力的输出进行进一步的处理。
残差连接和层归一化:Transformer 使用残差连接和层归一化来稳定训练过程,提高模型的性能。
2. Transformer 网络优点
2.1 并行计算
由于 Transformer 使用自注意力机制,它可以在计算每一个元素的新表示时并行处理所有的元素,这使得
Transformer 在训练和推理时都具有很高的效率。
2.2 捕捉长距离依赖
自注意力机制可以直接计算任意两个元素之间的相关性,因此 Transformer 能够有效地捕捉序列中的长距离依赖。
2.3 可解释性
由于自注意力机制的计算过程是可视化的,我们可以直观地看到模型在处理每一个元素时都关注了哪些元素,这使得
Transformer 具有很好的可解释性。
3. Transformer 网络缺点
3.1 计算资源消耗大
虽然 Transformer 可以并行计算,但是由于自注意力机制需要计算所有元素之间的相关性,因此
Transformer 的计算复杂度和内存消耗都较大。
3.2 难以捕捉局部信息
由于 Transformer 主要依赖全局的自注意力机制,它可能会忽视序列中的局部信息,这在某些任务中可能会导致性能下降。 |
