并行计算入门

作者：上班摸鱼的时候才水知乎

次浏览

次

2023-1-3

编辑推荐:

本文主要讲解了并行计算所依附的硬件架构及其相关的一些概念，通过 OpenMP, OpenMPI 和 CUDA 分别简单地介绍了基于共享内存，消息传递和 GPU（其实也是一种共享内存并行编程）三种方法的并行编程，关于并行计算的更多开发经验还需要在实践中积累。希望能为大家提供一些参考或帮助。
文章来自于知乎，由火龙果Linda编辑推荐。

1 概述

1.1 并行计算

高性能计算（High Performance Computing）是计算机科学中的一个领域，其目的可以概括为优化性能，它包括了缓存技术、数据结构和算法、IO 优化、指令重组（instruction reorganization）、编译器优化等；

并行计算（Parallel Computing）是高性能计算下的一个细分领域，其主要思想是将复杂问题分解成若干个部分，将每一个部分交给独立的处理器（计算资源）进行计算，以提高效率；针对不同的问题，并行计算需要专用的并行架构，架构既可以是专门设计的，含有多个处理器的单一硬件或超级计算机，也可以是以某种方式互连的若干台的独立计算机构成的集群；并没有一个统一的并行计算架构适用于每一个问题，如果使用了错误的架构，并行计算甚至会导致性能下降。

1.2 硬件架构

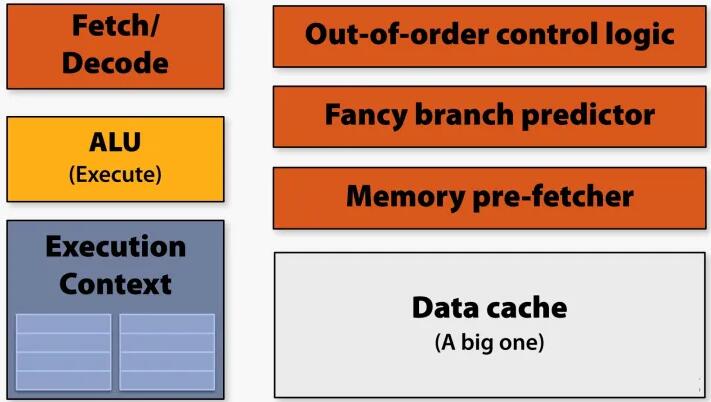
中央处理器（Central Processing Unit）的主要功能是解释计算机指令，它由控制单元（Control Unit）、算术逻辑单元（Arithmetic Logic Unit）、乱序控制单元（Out-of-Order Control Unit）、分支预测器（Branch Predictor）、数据缓存（Data Cache）等部件组成；CPU 被设计为可以快速地处理各种通用计算任务并最小化延迟，但在并发性（时钟频率）方面受到限制；

图形处理器（Graphics Processing Unit, GPU）是英伟达（NVIDIA）在 1999 年 8 月发布 NVIDIA GeForce 256 时提出的概念；现代 GPU 的模型设计可以概括为几个关键点：

GPU 的设计目的是最大化吞吐量（Throughput）

能够将程序中数据可并行的部分从 CPU 转移到 GPU

能够使用尽可能多的线程进行并行计算

GPU 拥有的内核数量相较于 CPU 多得多，可以有数千个同时运行的内核执行大规模并行计算，因此在早期专门应用于图形数据的处理，但随着近十几年的发展，其强大的并行处理能力也使其可以处理非图形数据，尤其在深度学习领域非常受欢迎；

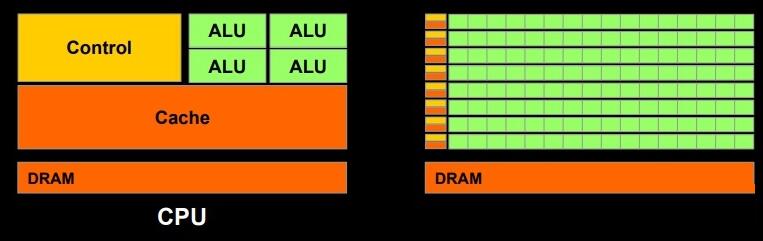
在制造工艺的限制下，芯片的密度和最大面积都是有限的（摩尔定律），因此芯片设计实际上是功能和元件数量的权衡；出于对通用性的要求，CPU 的芯片设计必须使用较多种类的原件以增加其功能，同时放弃部分具有复杂功能的元件数量，而 GPU 的芯片设计则是通过移除部分具有复杂功能的元件来换取更多的空间，并集成更多的基本功能元件；

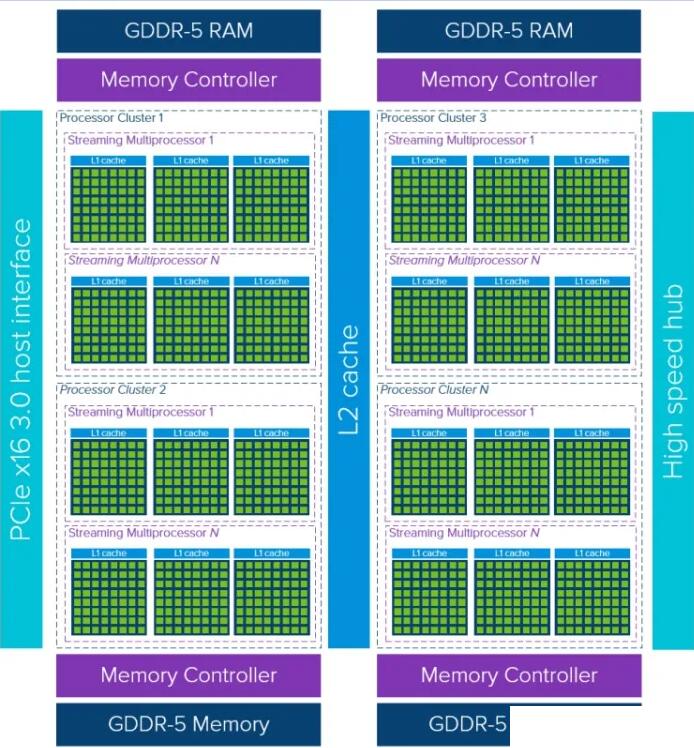
GPU 设备由多个流多处理器（Streaming Multiprocessor）的处理器集群（Processor Cluster）组成。每个流多处理器都关联一个控制单元和 L1 Cache，这样的设计使得一个芯片可以同时支持上百个指令流的并行执行；通常一个流多处理器在与全局 GDDR-5 内存交换数据之前都会利用与之关联 L1 Cache 和 L2 Cache 来减少数据传输的延迟；而又因为 GPU 通常拥有足够大的计算量，使得其不需要与 CPU 一样非常频繁地从内存中获取数据，因此 GPU 的缓存层一般是小于 CPU 的。

与 CPU 相比，GPU 可以使用较少且相对较小的内存缓存层。原因是 GPU 具有更多的专用于计算的晶体管，这意味着它无需担心从内存中获取数据需要多长时间。只要 GPU 拥有足够的计算量，就可以掩盖潜在的内存访问 “等待时间”，从而使其保持繁忙状态。

2 概念

2.1 访存模型

共享内存模型的的计算机中通常有非常多的内核，每个内核都有本地的处理器和缓存；相对的，在互联网络上或其它结点中的处理器和存储一般称为全局的；根据不同的互联网络和访问存储器的方式，一个共享内存机器可以被分为以下几类：

Uniform Memory Access

均匀存储访问（Uniform Memory Access, UMA）模型的特点是所有的处理器都拥有本地的高速缓存（L1 Cache, L2 Cache），所有的处理器都均匀地共享物理存储（Memory），并且每一个处理器访问任何存储字都需要相同的时间。

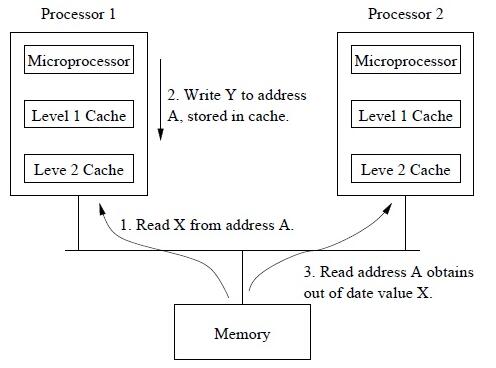
2. Non-Uniform Memory Access

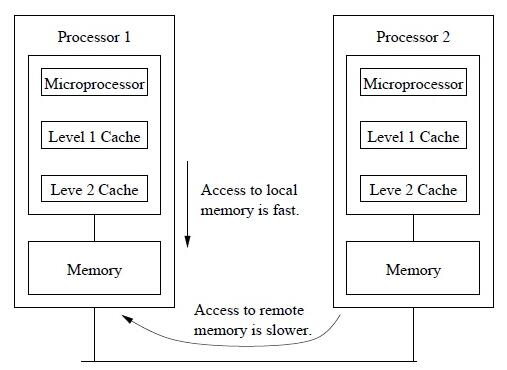
非均匀存储访问（Non-Uniform Memory Access, NUMA）模型的共享存储器在物理上是分布式的，所有的本地存储器构成了全局地址空间；处理器在访问本地存储器时的速度比访问全局存储器（共享存储器，或其他处理器的本地存储器）快，处理器访问内存的时间取决于内存相对于处理器的位置。

不同的处理器访问共享存储器时，位置的不同会导致访问延迟。

3. Cache-Only Memory Architecture

高速缓存存储结构（Cache-Only Memory Architecture, COMA）是将 NUMA 中的分布存储器换成了高速缓存，每个处理器上没有存储层次结构，所有的高速缓存共同构成了全局地址空间。

2.2 Flynn 分类法

Flynn 分类法（Flynn's Taxonomy）是一种高效能计算机的分类方式，他根据指令和数据的执行方式将计算机系统分成了四类：

单指令单数据模型（Single Instruction Single Data, SISD）

一般来说具有单核 CPU （不讨论超线程技术）的计算机就是基于单指令单数据模型的，对于每一个 CPU 时钟，CPU 按照 Fetch（从寄存器中获取数据），Decode（解码），Execute（执行并将结果保存在另一个寄存器中）的步骤顺序执行指令；上个世纪的计算机几乎都是 SISD 模型的。

2. 单指令多数据模型（Single Instruction Multi Data, SIMD）

单个控制单元拥有多个处理器，这些处理器上运行的线程共享同一个指令流，实现了时间上的并行；GPU 就是典型的 SIMD 模型。

3. 多指令单数据模型（Multi Instruction Single Data, MISD）

多个处理器分别拥有自己的控制单元并共享同一个内存单元，应用场景较少。

4. 多指令多数据模型（Multi Instruction Multi Data, MIMD）

多个控制单元异步地控制多个处理器，同时处理器可以在不同的数据上运行不同的程序，一般通过线程或进程层面的并行来实现，从而实现空间上的并行。

2.3 加速比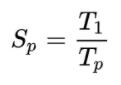

加速比（Speedup）用于衡量我们现在使用的并行算法比串行算法快了多少，也就是将程序并行化之后提升的效率，其公式是：

其中 p 代表 CPU 数量，T_1 代表使用串行算法的执行时间，T_p 代表当有 p 个处理器时使用并行算法的执行时间；当 S_p == p ，即 T_1 == p * T_p 时，S_p 称为线性加速比（Linear Speedup）。

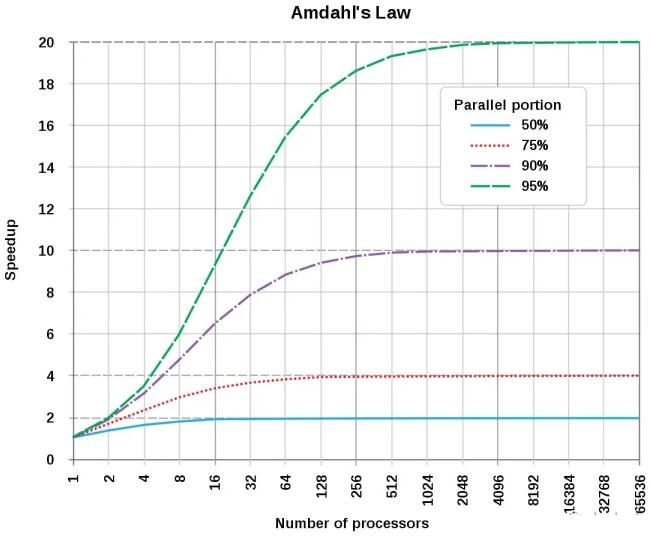
2. 阿姆达尔定律

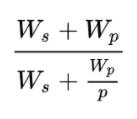
阿姆达尔定律（Amdahl's law）用于估计程序可以达到的最大加速比，W_s 和 W_p 分别表示程序串行部分和并行部分所占的百分比，W_s + W_p 表示程序串行执行的时间（此时并行部分 W_p 相当于被单个处理器执行），W_s + W_p/p 表示程序使用 p 个处理器执行的时间；当 p -> ∞ 时，其上限是 (W_s + W_p) / W_s。

c++ for (int i = 0; i < 1000000000; ++i) std::this_thread::sleep_for(std::chrono::seconds(1)); // sequential for (int i = 0; i < 1000000000; ++i) std::this_thread::sleep_for(std::chrono::seconds(1)); // parallel

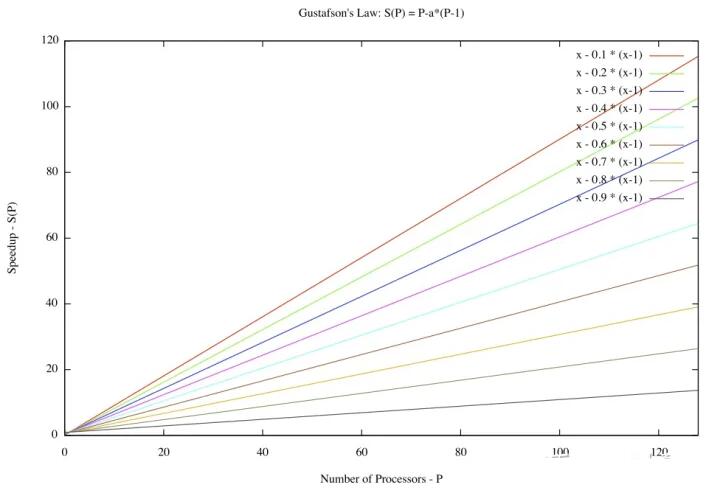
3. 古斯塔夫森定律

古斯塔夫森定律（Gustafson's Law）通过使用来描述加速比，p 代表处理器的数量，a 代表程序串行化的部分；

阿姆达尔定律描述的是增加处理起的数量并不一定能提高加速比，只有增加程序并行部分的比例，才能提高加速比。

古斯塔夫森定律描述的是随着程序并行化比例的提高，加速比与处理器个数成正比的比例（斜率）也在增加。

4. 性能

性能（Efficiency）是由加速比派生出的量度性能的指标，它可以表示每个处理器的加速比，即每个处理器在这个算法中的利用率，其公式是：

5. 时钟加速比

S(p) = t_s / t_p

时钟加速比（Speedup in Wall-Clock Time）的公式很简单，用使用串行算法花费的时钟时间除以使用并行算法花费的时钟时间即可，但是因为时钟时间包括了网络延迟，IO，缓存争用等无关因素，所以它与加速比和算法的复杂度并不相关，只能用于粗略地衡量加速比。

3 并行计算框架

3.1 OpenMP

OpenMP（Open Multi-Processing）是一套针对多处理器共享内存机器进行多线程并行编程的 API，支持的语言有 C，C++ 和 Fortran，支持的编译器有现在主流的 GCC 和 Clang 等；

OpenMP 提供了用于描述并行编程的高层抽象，使用 OpenMP 最大的好处在于，当我们没有在编译的时候加上 OpenMP 相关的选项，或当编译器不支持 OpenMp 时，程序仍然可以完成编译，并使用串行的流程正常地运行；这在很大程度上降低了并行编程的难度，使得我们可以把更多的精力投入到并行算法本身，而非其实现细节；尤其对基于数据集进行并行划分的程序，OpenMP是一个很好的选择。

Directive

所有的 OpenMP 编程操作都是基于 #pragma omp 宏指令（directive）的，每个 directive 都会被转换为与其相应的 OpenMP 库函数调用，而 OpenMP 会处理与线程线程调用相关的操作，包括线程的 fork, join, synchronizing 等，下面是一个简单的例子：

#include <omp.h>
#include <iostream>

int main()
{
#pragma omp parallel
{
int tid{ omp_get_thread_num() };
printf("Hello world from thread %d\n", tid);

int thread_num{ omp_get_num_threads() };
if (tid == thread_num - 1)
{
printf("tid: %d, thread_num: %d\n", tid, thread_num);
}
}
return 0;
}

注意链接的时候需要加上 -fopenmp，这是一个高层级的标志，其作用主要是链接 gomp 库（GCC 的 OpenMP 实现，如果使用 clang 进行编译则会链接 llvm 对应的实现，类似于 libstdc++ 和 libc++ 的区别），OpenMP 通常是基于 pthread 实现的，所以 gomp 库还会链接更多的库来使用操作系统的线程功能：

[joelzychen@DevCloud ~/parallel-computing]$ g++ -std=c++11 -g -o openmp-case openmp-case.cpp -fopenmp
[joelzychen@DevCloud ~/parallel-computing]$ ./openmp-case
Hello world from thread 5
Hello world from thread 2
Hello world from thread 1
Hello world from thread 3
Hello world from thread 7
tid: 7, thread_num: 8
Hello world from thread 4
Hello world from thread 0
Hello world from thread 6

omp_get_thread_num() 和 omp_get_num_threads() 两个函数的名称非常直白，分别获取了当前线程的 ID（这个 ID 是 OpenMP 管理的，并不是 PID）和总的线程数；#pragma omp parallel 是最基本的 directive，它可以启动一组线程并让他们并行地执行，如果我们没有在使用 #pragma omp parallel 这个 directive 的时候指定线程数量，那么默认会启动等同于 CPU 核心数量的线程数；并且由于程序是并行地执行的，所以我们并不能保证程序执行的顺序；

Example

再看一个例子：

#include <omp.h>
#include <iostream>
#include <thread>
#include <chrono>

constexpr int thread_num = 3;
using namespace std;

int main()
{
std::chrono::steady_clock::time_point time_begin = std::chrono::steady

_clock::now();

#pragma omp parallel for schedule(static) num_threads(thread_num)
for (int i = 0; i < thread_num; ++i) std::this_thread::sleep_for(std::

chrono::seconds(1));

std::chrono::steady_clock::time_point time_end = std::chrono::steady

_clock::now();
cout << "time: " << std::chrono::duration_cast<std::chrono:

:milliseconds>(time_end - time_begin).count() << " ms" << endl;

return 0;
}
[joelzychen@DevCloud ~/parallel-computing]$ g++ -std=c++11

-g -o openmp-case openmp-case.cpp -fopenmp
[joelzychen@DevCloud ~/parallel-computing]$ ./openmp-case
time: 1000 ms
[joelzychen@DevCloud ~/parallel-computing]$ g++ -std=c++11

-g -o openmp-case openmp-case.cpp
[joelzychen@DevCloud ~/parallel-computing]$ ./openmp-case
time: 3000 ms

因为时间粒度只精确到了毫秒级，所以只能够看到大致的运行时间是 1s 和 3s；num_threads(thread_num) 用于指定线程数量，schedule(static) 用于指定将 for 循环中的迭代以静态的方式分配给多个线程，假设有 n 次循环迭代，t 个线程，那么将给每个线程静态地分配 n/t 次迭代进行运算。

OpenMP 还提供了 barrier（等待所有线程执行完前面的所有计算），atomic（原子操作），flash（写入内存）等各种操作；关于 OpenMP 所有的函数和 directive 可以参考 OpenMP 4.5 API C/C++ Syntax Reference Guide。

3.2 OpenMPI

OpenMPI (Open Message Passing Interface) 是基于消息队列进行进程间通信的并行编程库，MPI 是一个跨语言的通信协议，OpenMPI 只是遵循这种协议的一种实现；在基于消息队列的并行编程模型中，每个进程都有一个独立的地址空间，一个进程不能直接访问其他进程中的数据，而只能通过消息传递的方式来实现进程间的通信，我们需要显式地通过发送和接受消息来实现处理器之间的数据交换；使用消息队列进行通信的开销比共享内存大，因此它主要用来进行大粒度并行编程的开发。

API

MPI 有几个最基础的函数，在每一个 MPI 并行程序中几乎都会用到这几个函数：

int MPI_Init (int* argc ,char** argv[] )

初始化 MPI 环境，一般是第一个被调用的 MPI 函数；

int MPI_Finalize (void)

终止 MPI 环境，一般是最后一个被调用的 MPI 函数；

int MPI_Comm_size (MPI_Comm comm ,int* size )

获取通信组进程的个数，MPI_Comm comm 是指定的 communicator，共享通信空间的一组进程组成了通信组，通信组中的所有进程由 communicator 管理；

int MPI_Comm_rank (MPI_Comm comm ,int* rank)

获取当前进程在通信组中的进程 ID，这个 ID 是由 communicator 管理的，不是 PID；

Example

来看一个例子，尝试用 OpenMPI 解决 0-1 背包问题，假设物品的数量是 N，背包的容量是 C，第 i 个物品的重量是 weight[i]，价值为 value[i]，先用常规的线性 DP 解决：

#include <cstring>
#include <iostream>
#include <fstream>
#include <vector>
#include <thread>
#include <chrono>
#include <omp.h>

using namespace std;

int main()
{
std::chrono::steady_clock::time_point time_begin

= std::chrono::steady_clock::now();

fstream input_file("input-knapsack.txt");
int N;
int64_t Capacity;
input_file >> N >> Capacity;
int64_t weight[N], value[N];
for (int i = 0; i < N; ++i)
input_file >> weight[i] >> value[i];

vector<vector<int64_t>> dp(N + 1, vector<int64

_t>(Capacity + 1));
for (int i = 0; i <= N; ++i)
{
#pragma omp parallel for
for (int64_t j = 0; j <= Capacity; ++j)
{
if (i == 0 || j == 0)
dp[i][j] = 0;
else if (j < weight[i - 1])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]]

+ value[i - 1]);
}
}
cout << "max value: " << dp[N][Capacity] << endl;

std::chrono::steady_clock::time_point time_end = std::

chrono::steady_clock::now();
cout << "time: " << std::chrono::duration_cast<std::

chrono::milliseconds>(time_end - time_begin).count

() << endl;
return EXIT_SUCCESS;
}

先用背包数据随机生成器（见附录）生成数据，然后编译运行，对比一下使用 OpenMPI 前后的结果：

[joelzychen@DevCloud ~/parallel-computing]$ g++

-std=c++11 -g -o knapsack-generator knapsack

-generator.cpp -lcrypto
[joelzychen@DevCloud ~/parallel-computing]$

./knapsack-generator 1000 8000
[joelzychen@DevCloud ~/parallel-computing]$

g++ -std=c++11 -g -o knapsack knapsack.cpp
[joelzychen@DevCloud ~/parallel-computing]$

./knapsack
max value: 13093
time: 175 ms
[joelzychen@DevCloud ~/parallel-computing]$

g++ -std=c++11 -g -o knapsack-openmp

knapsack.cpp -fopenmp
[joelzychen@DevCloud ~/parallel-computing]

$ ./knapsack-openmp
max value: 13093
time: 75

现在使用 OpenMPI 来改造 0-1 背包问题的 DP 解法：

#include <cstring>
#include <iostream>
#include <fstream>
#include <vector>
#include <thread>
#include <chrono>
#include <mpi.h>

using namespace std;

int main(int argc, char *argv[])
{
std::chrono::steady_clock::time_point time_begin

= std::chrono::steady_clock::now();

MPI_Init(&argc, &argv);
MPI_Comm comm = MPI_COMM_WORLD;
int rank, size;
MPI_Comm_rank(comm, &rank);
MPI_Comm_size(comm, &size);
MPI_Status status; // MPI receive
MPI_Request request; // MPI send

fstream input_file("input-knapsack.txt");
int N;
int64_t Capacity;
if (rank == 0)
input_file >> N >> Capacity;
MPI_Bcast(&N, 1, MPI_INT, 0, comm);
MPI_Bcast(&Capacity, 1, MPI_LONG, 0, comm);
MPI_Barrier(comm);

int64_t weight[N], value[N];
if (rank == 0)
for (int i = 0; i < N; ++i)
input_file >> weight[i] >> value[i];
MPI_Bcast(weight, N, MPI_LONG, 0, comm);
MPI_Bcast(value, N, MPI_LONG, 0, comm);
MPI_Barrier(comm);

vector<vector<int64_t>> dp(N + 1, vector<int64

_t>(Capacity + 1));
int64_t prev_max_value; // mpi send and receive variable

for (int i = 0; i <= N; ++i) // for each item from 0 to n
{
for (int64_t j = rank; j <= Capacity; j += size) // for

each capacity from 0 to Capacity, each thread compute

its own rows
{
if (i == 0 || j == 0)
dp[i][j] = 0;
else if (j < weight[i - 1])
dp[i][j] = dp[i - 1][j];
else
{
// int MPI_Recv(void *buf, int count, MPI_Datatype

datatype, int source, int tag, MPI_Comm comm,

MPI_Status *status)
MPI_Recv(&prev_max_value, 1, MPI_LONG,

(j - weight[i - 1]) % size, i - 1, comm, &status);
dp[i][j] = max(dp[i - 1][j], prev_max_value +

value[i - 1]);
}

// send dp[i][j] to the next nodes that may need

this curr_max_value
if (i < N && weight[i] + j <= Capacity)
{
// int MPI_Isend(const void *buf, int count,

MPI_Datatype datatype, int dest, int tag,

MPI_Comm comm, MPI_Request *request)
MPI_Isend(&dp[i][j], 1, MPI_LONG,

(j + weight[i]) % size, i, comm, &request);

// asynchronous operation
}
}
MPI_Barrier(MPI_COMM_WORLD);
}
MPI_Barrier(MPI_COMM_WORLD);

if (rank == Capacity % size)
printf("max value: %ld\n", dp[N][Capacity]);

if (rank == 0)
{
std::chrono::steady_clock::time_point time_end

= std::chrono::steady_clock::now();
printf("time: %ld ms\n", std::chrono::duration_

cast<std::chrono::milliseconds>(time_end - time_begin).count());
}
MPI_Finalize();
return EXIT_SUCCESS;
}

相比于 OpenMP，使用 OpenMPI 解决背包问题的过程非常复杂，首先要使用 rank == 0 的线程处理输入，然后将输入的 N, C 和 weight, value 数组都广播给其他线程，之后开始处理 dp 数组，动态规划的步骤分为以下几步：

对于从 0 到 n 的每一件物品 i 串行执行；

对于第 j 个线程（j = rank, 0 <= j < size），使其去处理对应的 capacity (capacity == j)，之后让 j += size 处理下一件；

i == 0 或 j == 0 时初始化边界为 0；

如果 j < weight[i - 1]，此时背包容量小于 weight[i - 1]，那么 dp[i][j] = dp[i - 1][j]；

如果 j <= weight[i - 1]，此时背包容量大于等于 weight[i - 1]，那么此时 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1])，但是由于容量大小为 j - weight[i - 1] 时的 dp 结果（也就是 dp[i - 1][j - weight[i - 1]]）不一定是由第 j 个线程处理的，所以本地的 dp[i - 1][j - weight[i - 1]] 不一定含有正确的值，所以需要通过 mpi 从第 (j - weight[i - 1]) % size 个线程拿到对应的值（也就是 prev_max_value）之后再做处理；

对于下一件物品，当背包容量为 j + weight[i] 时可能会用到当前的 dp 结果，因此需要将 dp[i][j] 发送给处理容量为 j + weight[i] 的第 (j + weight[i]) % size 个线程；

最后处理结果时只需要让处理了 dp[N][Capacity] 的第 rank = Capacity % size 个线程输出即可；注意这个做法会有 bug，如果输入中的第 i 个物品的 weight[i] == 0，那么线程在等待 recv 的时候会从自己这个线程接收一个值，从而导致结果不对；

使用 OpenMPI 前先要从官方网站下载源码并安装（或者通过 yum 安装），然后使用 mpic++ 进行编译，使用 mpirun 运行：

[joelzychen@DevCloud ~/parallel-computing/openmpi]$

sudo find / -name "mpic++"
/usr/lib64/openmpi/bin/mpic++
/usr/lib64/mpich/bin/mpic++
[joelzychen@DevCloud ~/parallel-computing]$ /usr/lib64

/mpich/bin/mpic++ -g -std=c++11 -o knapsack-openmpi

knapsack-openmpi.cpp
[joelzychen@DevCloud ~/parallel-computing]$ /usr/lib64/

mpich/bin/mpirun -n 1 ./knapsack-openmpi
max value: 13093
time: 6694 ms
[joelzychen@DevCloud ~/parallel-computing]$ /usr/lib64

/mpich/bin/mpirun -n 2 ./knapsack-openmpi
max value: 13093
time: 4863 ms
[joelzychen@DevCloud ~/parallel-computing]$ /usr/lib64

/mpich/bin/mpirun -n 4 ./knapsack-openmpi
max value: 13093
time: 3674 ms
[joelzychen@DevCloud ~/parallel-computing]$ /usr/lib64/

mpich/bin/mpirun -n 8 ./knapsack-openmpi
max value: 13093
time: 2487 ms

横向比较 OpenMPI 和串行算法，在使用 OpenMPI 做 DP 的时候因为在消息传输中浪费了很多时间，其效率甚至不如串行算法；但如果使用穷举算法解 0-1 背包（在 OJ 里会超时的那种），再用 OpenMPI 优化的话，效率会有非常大的提升，有兴趣的同学可以自己了解一下；纵向比较开启不同线程数量的 OpenMPI 算法，我们在收发消息数量不变的情况下提升了同时进行运算的线程数量，因此明显地提高了效率；关于 OpenMPI 的所有函数可以查阅 Open MPI v4.0.4 documentation。

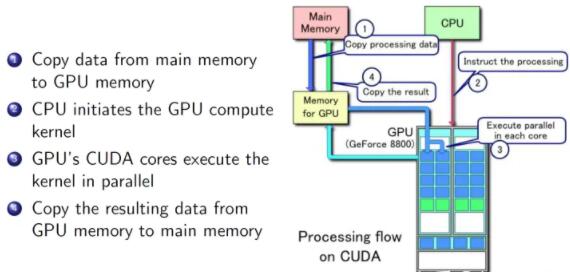
3.3 CUDA

CUDA 的全称是 Compute Unified Device Architecture，它是一个用于并行计算的平台和 API，它允许开发人员使用支持 CUDA 的 GPU 进行并行编程；GPU 并不能独立进行运算，它需要与 CPU 通过 PCIe 总线连接到一起协同进行工作，使用 GPU 进行的并行计算可以被视为是 CPU 和 GPU 的异构计算架构，CPU 负责处理逻辑复杂的串行部分，GPU 负责处理数据密集的并行部分，其中 CPU 通常被称为 host 主机端，GPU 通常被称为 device 设备端；

Kernel

CUDA 中的 kernel 核函数是在 GPU 端并行执行的函数，这个函数只包含程序的并行部分，它会被 GPU 上的诸多线程并行执行；相比于 CPU 上的线程，GPU 上的线程更加轻量级，创建的成本更小，线程切换更灵活，进入 CUDA 核函数时程序可以定义非常多的虚拟线程，但能够并行执行的硬件线程数也是有限的；一般来说基于 CUDA 程序的执行流程如下：

host 端进行内存分配和数据初始化，执行程序串行部分

device 端进行内存分配，并从 host 端拷贝数据到 device 端

device 端调用并执行核函数，同时使用缓存提升效率

device 端将运算好的结果拷贝到 host 端上

device 端释放内存，等待下一次核函数调用

Thread Hierarchy

CUDA 执行核函数的时候开启的线程拥有三层的层级结构：

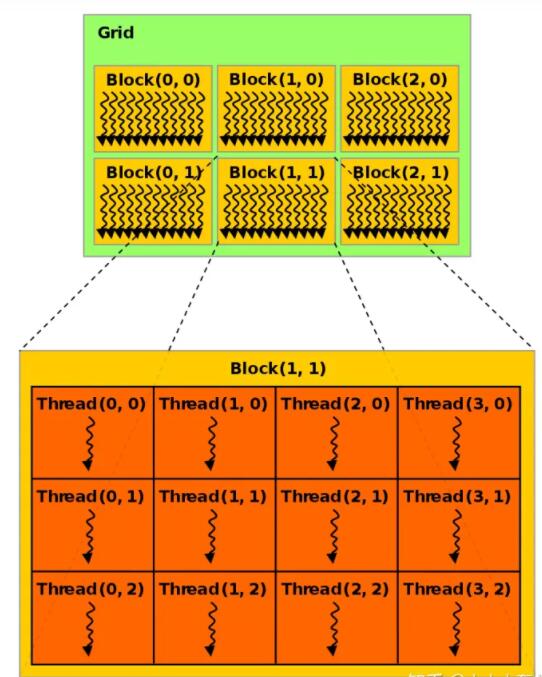
grid 是一个逻辑实体，可以理解为一个工作区，它运行在整个 GPU 上，同一个 grid 里的所有 thread 共享全局内存空间；

thread block

thread block 是一组并行执行的线程，一个 block 在单个 streaming multi-processor 中运行，即一个 block 中的所有 thread 都在这个流式多处理器中运行，它们可以通过共享内存或同步原语进行通信，位于不同的 block 中的 thread 一般来说不能互相通信和协作，每一个 block 都应该能够独立运行；

thread

thread 在 CUDA core 上执行，正如前文所说，GPU 上的线程非常轻量级，可以通过较大的寄存器提供非常快速的上下文切换（CPU 的线程句柄存在于较低的内存层次结构中，例如高速缓存）；

我们在调用核函数的时候需要通过 <<<block, thread>>> 的方式来指定 block 和 thread 的数量和维度。

Example

来看一个简单的例子，先串行地进行大约 10 亿次加法运算：

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <chrono>
#include <thread>

using namespace std;
constexpr uint64_t magic_number = 12345;

void Add(int n, uint64_t *x)
{
for (int i = 0; i < n; ++i)
x[i] += x[i];
}

int main(void)
{
int n = 1<<30;
uint64_t *x = (uint64_t *)malloc(n * sizeof(uint64_t));
memset(x, magic_number, sizeof(x));

std::chrono::steady_clock::time_point time_begin =

std::chrono::steady_clock::now();
Add(n, x);
std::chrono::steady_clock::time_point time_end =

std::chrono::steady_clock::now();
cout << "time: " << std::chrono::duration_cast<

std::chrono::milliseconds>(time_end - time_begin)

.count() << " ms" << endl;

free(x);
return 0;
}

为了方便对比，在 Windows PowerShell 中使用 nvcc 编译运行：

PS G:\> nvcc -o add .\add.cpp -ccbin "C:\Program

Files (x86)\Microsoft Visual Studio\2017\Professional\

VC\Tools\MSVC\14.16.

27023\bin\Hostx64\x64"
add.cpp
PS G:\> .\add.exe
time: 4472 ms

可以看到 Add 函数串行执行的时间大约是 4472 ms，现在我们将其修改为使用 CUDA 的并行程序：

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <chrono>
#include <thread>
#include <string>

using namespace std;
constexpr int magic_number = 12345;

__global__ void Add(int n, int *x)
{
for (int i = 0; i < n; ++i)
x[i] += x[i];
}

int main(void)
{
int n = 1<<30;
int64_t byte_size = n * sizeof(int);
int *x;
x = (int*)malloc(byte_size);
for (int i = 0; i < n; ++i)
x[i] = magic_number;

int *cuda_x;
cudaMalloc((void**)&cuda_x, byte_size);

// copy from host to device
cudaMemcpy(cuda_x, x, byte_size,

cudaMemcpyHostToDevice);

std::chrono::steady_clock::time_point time

_begin = std::chrono::steady_clock::now();
Add<<<1, 1>>>(n, cuda_x);
cudaDeviceSynchronize();
std::chrono::steady_clock::time_point time_end

= std::chrono::steady_clock::now();

// copy from device to host
cudaMemcpy(x, cuda_x, byte_size,

cudaMemcpyDeviceToHost);

// check result
bool result{ true };
for (uint32_t i = 0; i < n; ++i)
result = (result && (x[i] == magic_number

+ magic_number));
string result_str = (result ? "true" : "false");

cout << "result: " << result_str << endl;
cout << "time: " << std::chrono::duration_cast

<std::chrono::milliseconds>(time_end - time_begin)

.count() << " ms" << endl;
free(x);
cudaFree(cuda_x);
return 0;
}
PS G:\> nvcc -o cuda-add .\cuda-add.cu -ccbin "C:\

Program Files (x86)\Microsoft Visual Studio\2017\

Professional\VC\Tools\MSVC\14.16.

27023\bin\Hostx64\x64"
cuda-add.cu
Creating library cuda-add.lib and object cuda-add.exp
PS G:\> .\cuda-add.exe
result: true
time: 21904 ms

可以看到 CUDA 程序里有一些特殊的关键字和 API：

__global__ 是核函数的标志，只要在函数签名前加上 __global__ 它就可以被 CUDA 编译器分析为核函数；

因为 Add 函数是在 device 端运行的，我们需要先使用 malloc 和 cudaMalloc 分别为 host 和 device 端分配内存，然后使用 cudaMemcpy 将在 host 端初始化的数据拷贝到 device 端；

我们需要在 device 端调用 Add 核函数，这个操作对于 host 端来说是异步的，它不会等待 device 端的执行结果，我们需要调用 cudaDeviceSynchronize 函数来等待 device 端执行完毕并返回；如果我们连续调用了多个核函数，又没有在 device 端指定控制流，那么这些核函数只会在 device 端按顺序执行；

device 端执行完之后，使用 cudaMemcpy 将数据从 device 端拷贝回 host 端进行验证；

最后分别调用 free 和 cudaFree 来释放内存；

我们的程序虽然跑在 GPU 上，但速度反而比跑在 CPU 上的时候更慢了，因为我们只为 kernel 分配了 1 个 block 和 1 个 thread (Add<<<1,1>>>(n, x);)，既没有发挥 GPU 并行计算的优势，又浪费了时间在 CPU 和 GPU 的交互上；优化的方法和 OpenMPI 中的例子类似，只需要让每个线程处理对应自己的数据，并在循环中每次自增一个步长：

__global__ void Add(int n, int *cuda_x)
{
int index = blockIdx.x * blockDim.x + threadIdx.x;
int stride = blockDim.x;
for (int i = index; i < n; i += stride)
cuda_x[i] += cuda_x[i];
}

int main(void)
{
// ...
Add<<<4096, 256>>>(n, cuda_x);
// ...
}

其中：

blockIdx.x 代表 block 的 ID，即当前 block 的下标；

blockDim.x 代表 block 的维度，即一个 block 内含有多少个 thread；同时也是步长 stride；

类似的，threadIdx.x 代表 thread 的 ID，即当前 block 的下标；

index 是当前需要进行运算的数据在内存中的位置

在这个例子中，我们开启了 4096 个 block 和 256 个 thread，即 blockIdx.x < 4096, blockDim.x == 256, threadIdx.x < 256；

当然如果申请过多的 block 并不会提升运算的效率，因为 cuda core 会浪费许多时间来调度这些 block；我们可以多次修改 <<<block, thread>>> 来对比在使用不同数量的 block 和 thread 的情况下的性能：

# Add<<<4096, 256>>>(n, x);
PS G:\> nvcc -o cuda-add .\cuda-add.cu -ccbin

"C:\Program Files (x86)\Microsoft Visual Studio\2017\

Professional\VC\Tools\MSVC\14.

16.27023\bin\Hostx64\x64" cuda-add.cu
Creating library cuda-add.lib and object cuda-add.exp
PS G:\> .\cuda-add.exe
result: true
time: 159454 ms

# Add<<<1, 256>>>(n, x);
PS G:\> .\cuda-add.exe
result: true
time: 1038 ms

# Add<<<1, 1024>>>(n, x);
PS G:\> .\cuda-add.exe
result: true
time: 299 ms

关于 CUDA 的更多使用说明可以参考 CUDA Toolkit Documentation。

4 总结

本文主要讲解了并行计算所依附的硬件架构及其相关的一些概念，通过 OpenMP, OpenMPI 和 CUDA 分别简单地介绍了基于共享内存，消息传递和 GPU（其实也是一种共享内存并行编程）三种方法的并行编程，关于并行计算的更多开发经验还需要在实践中积累。

5 附录

0-1 背包问题随机数据生成器

// knapsack-generator.cpp
#include <iostream>
#include <fstream>
#include <openssl/rand.h>

using namespace std;

int main (int argc, char *argv[])
{
if (argc < 3)
{
fprintf(stderr, "usage: %s N C\n", argv[0]);
exit(1);
}

int N = stoi (argv[1]);
uint64_t C = stoi (argv[2]);

int m = 4 * C / N;
unsigned char buff[2 * N];
RAND_seed(&m, sizeof(m));
RAND_bytes(buff, sizeof(buff));

ofstream file_stream;
file_stream.open("input-knapsack.txt");
file_stream << N << ' ' << C << endl;
for (int i = 0; i < N; i++)
{
file_stream << buff[2 * i] % m << ' ' << buff[2 * i +

1] % m << endl;;
}
file_stream.close();

return 0;
}

次浏览