| 编辑推荐: |
本文主要介绍用CUDA实现矩阵乘法运算(C = A x B)的几个基本方法,帮助大家理解矩阵在GPU上面的运算与CPU上的有何异同,通过实践上手CUDA的优化计算,相比基础方法,能提速10倍以上。
文章来自于微信公众号极市平台,由火龙果Linda编辑推荐。 |
|
本文内容涉及到CUDA矩阵1D运算、2D运算、共享内存、CUBLAS的使用。
V100上的测试对比:
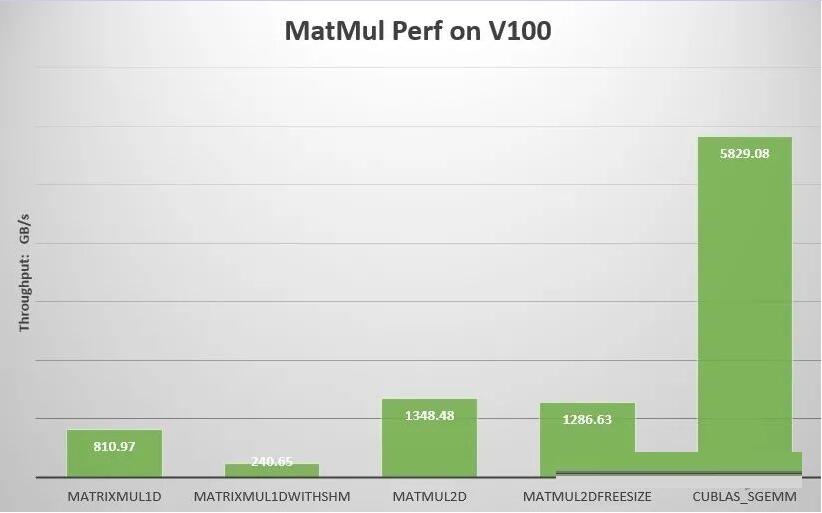
1 CPU矩阵乘运算
矩阵 C = A x B的数学运算,是线性代数里面最基本的内容, 计算的基本公式如下:
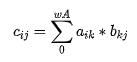
矩阵C 中每个元素 为A 的第 1 行与B 的j 列进行元素对应相乘再求和。
若:A 宽wA 高:hA; B 宽wB 高:hB; C 宽wC 高:hC 有: 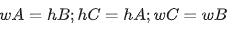
通过计算机运算我们能够很容易的得到运算部分的代码,如下:
for (unsigned int i = 0; i < hA; ++i){
for (unsigned int j = 0; j < wB; ++j) {
float Cij = 0;
for (unsigned int k = 0; k < wA; ++k) {
Cij += A[i][k] * B[k][j];
}
C[i][j] = Cij ;
}
}
|
进一步,我们还需要了解矩阵的一维数据运算方式。矩阵的数据在内存中存储的格式是线性格式(行优先/列优先),如下所示,展示的是一种行优先的存储方式。可以通过索引计算来定位矩阵中的某个元素,比如第i行第j列的元素,在线性内存中的位置:i
* w + j。w为矩阵的宽度。
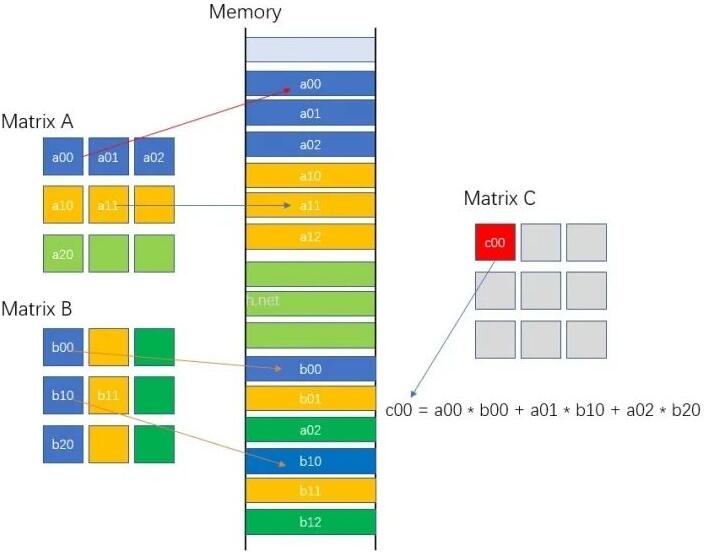
运算的CPU实现代码 如下所示:
void matrixMulCPU(float *C, const float
*A, const float *B, unsigned int wA,
unsigned int wC, unsigned int hC){
unsigned int hA = hC;
unsigned int wB = wC;
for (unsigned int i = 0; i < hA; ++i)
for (unsigned int j = 0; j < wB; ++j) {
double sum = 0;
for (unsigned int k = 0; k < wA; ++k) {
sum += (double)A[i * wA + k] * (double)
B[k *+ j];
}
C[i * wB + j] = (float)sum;
}
} |
上述代码采用三重循环实现了全部运算。最内层是计算每个Cij元素运算,再用两个for遍历获得了整个C矩阵的结果。显然,如果用单线程的CPU运算,该过程的计算时间是
其中hA、wA是矩阵A的高和宽,wB是矩阵B的宽度,deltaT表示每次运算消耗的时间。
由于过程只有一个CPU线程在串行计算,所以矩阵越大耗时越久。为了优化这个过程,我们采用GPU来计算,GPU有大量的线程,通过增加更多的线程来并行计算,降低运算时间。理论上当我们用N个线程来运算时,整个运算时间为:
2 一维块(1D block)构建运算
多线程编发计算道理很简单,让多个线程分担一个线程的工作量。在NVIDIA的GPU中使用多线程不像CPU中并行一样直接,如C++添加“#pragma
omp parallel“。GPU中运算涉及数据的转移(CPU <-> GPU)、GPU工作流的创建等内容,但最核心的点是线程thread的运算过程。基本上,我们只需要明确两个问题:
> CUDA代码里面的Thread是如何调用的?
> 如何让不同的Thread与需要计算的数据匹配?
2.1 问题1: CUDA代码里面的Thread是如何调用的?
CUDA对thread的调用其实由编译器完成的。用户在编写代码时主要关注如何定义GPU能运行的函数,其次是如何调用这个函数。定义GPU线程(Thread)可运行函数,实际上就是在函数前面加上一个'\__global\__'的前缀:
__global__ void functionExample() {
// code part.
} |
函数的执行需要用一个特殊的语法"<<<...>>>"
在主机host上面执行上述函数,尖括号里面实际上是定义执行这个函数用多少线程threads
functionExample<<<numBlocks, threads PerBlock>>> (); |
这里需要知道如果调用上述函数,那么每个Thread都会去执行functionExample这个函数。
Thread有多少?
thread总数量
= grids的数量 *
一个grid里面block数量 *
一个block里面threads的数量。 |
CUDA里面用Grid和Block作为线程组织的组织单位,一个Grid可包含了N个Block,一个Block包含N个thread。
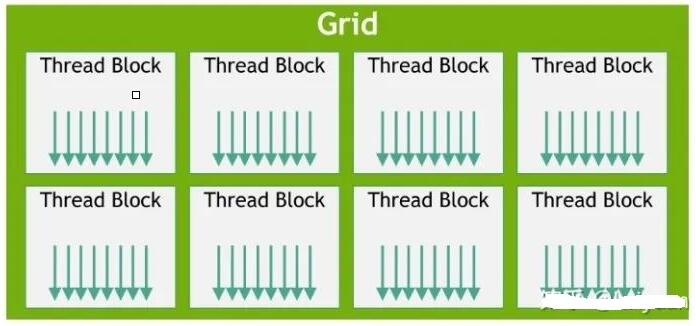
示例的Grid包含8个block,每个block包含8个thread
在C++代码中(主机运行代码中)调用CUDA的多线程函数,一般过程是标记函数、设置线程数、执行函数。这里放一个CUDA
GUIDE里面的样例代码:
__global__ void MatAdd(float A[N][N],
float B[N][N],float C[N][N])
{
int i=blockIdx.x*blockDim.x+threadIdx.x;
int j=blockIdx.y*blockDim.y+threadIdx.y;
if (i < N && j < N)
C[i][j] = A[i][j] + B[i][j];
}
int main()
{
...
// Kernel invocation
dim3 threadsPerBlock(16, 16);
// 定义一个block里面有多少thread 16*16
dim3 numBlocks(N / threadsPerBlock.x,
N / threadsPerBlock.y);
MatAdd<<<numBlocks, threadsPerBlock>>>
(A, B, C);
...
}
|
2.2 问题2:如何让不同的Thread与需要计算的数据匹配?
既然有这么多的Thread去计算相同块的数据,会不会算重复或者漏算?现在是已知条件是:
一批GPU的Threads
一批待运算数据
我们需要做的是让数据与Thread对应起来。这里就涉及到了thread的编号。
thread的一维索引的计算相对简单,一般:
int thID = threadIdx.x + blockIdx.x * blockDim.x; |
计算示例如下,展示了获取第6个block里面的第5个thread的索引计算:
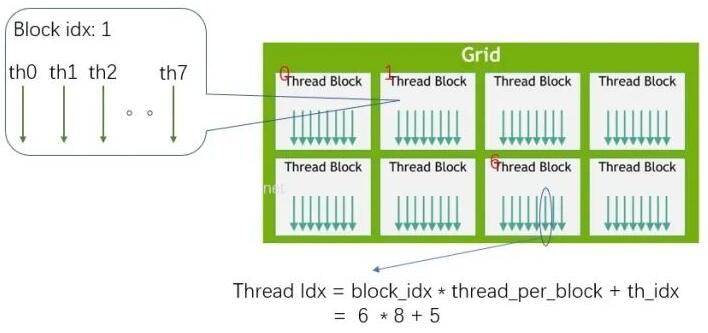
若对thread进行二维编号,那么每个thread的编号(索引)计算就需要多一个维度编号。在前面MatAdd示例中展示的就是二维的thread索引计算。
int i = blockIdx.x * blockDim.x + threadIdx.x;
int j = blockIdx.y * blockDim.y + threadIdx.y; |
这样获得了这个thread的索引Idx, 函数里面需要用户自行去确定索引与数据的对应关系。即,用户要根据Idx,自己分配thread与计算数据映射关系。
2.3 代码的基本实现
根据矩阵运算CPU的代码,我们得到GPU运算的代码如下所示
__global__ void MatMulKernel1D(float *C,
float *A, float *B, const int wh,
const int wC, const int hC)
{
const int totalSize = wC * hC;
int thID = threadIdx.x + blockIdx.x *
blockDim.x;
// 索引计算
while (thID < totalSize) {
int Cx = thID / wC;
//数据坐标 与 thread索引的映射
int Cy = thID % wC;
float rst = 0.0;
for (int i = 0; i < wh; i++) {
rst += A[Cx * wh + i]*B[i*wC + Cy];
}
C[Cx * wC + Cy] = rst;
thID += gridDim.x * blockDim.x;
}
}
|
相比CPU的code,主要的不同点:
for循环由三层变为了一层(不算while循环);
增加了一个thread的索引计算(thID);
每个thread完成1个(或多个)C矩阵中元素的计算;
while循环是为了在总threads数量不等于C矩阵元素总数量时,防止"数据计算不足"或者"访问越界";
2.4 共享内存优化计算
上述过程中我们已经实现了CUDA对矩阵的计算,为了进一步优化运算。需要使用一些加速手段,这里最常用的方式是使用共享内存。共享内存是一种片上内存,它的访问速度与L1相同。共享内存特点可参看GPU显存理解。关键特点:
一个Block内的thread都能访问;
c++中通过 \__shared\__ 关键字定义;
对于一些访问频率高的数据,可以从全局内存转移到共享内存中,这样能够提升运算速度。在矩阵乘法中(C=A
x B),要获得C矩阵的某一行(比如i行)数据,A矩阵中的i行数据需要与B矩阵的所有列数据都相乘一次。一般而言,数据都是在运算中从全局内存加载到寄存器中,那么A矩阵的i行数据在本次运算中需要加载B的列次(假设B有K列)。如果有共享内存,我们只需要将该数据从全局内存加载一次到共享内存,然后再反复使用。数据传输方式由:
(Global memory -> L2 -> L1 -> register)
* K * factor1
变为:
Global memory -> shared memory
+ ( shared memory ->
register) * K * factor2
下图展示K=3的例子:
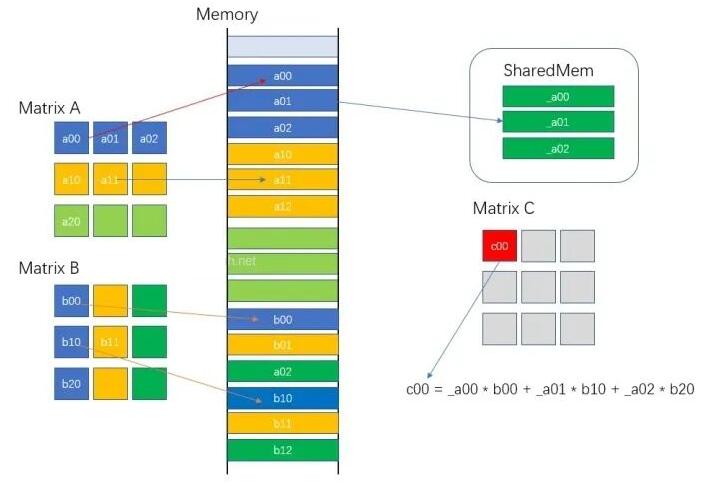
共享内存提速内存访问速度
所以每次运算,我们将A矩阵的i行放入到共享内存中,保证第i行数据不会反复从Global中加载,从而提升运算速度。函数代码片段如下:
template <int shWASize>
__global__ void MatMulKernel1DWithShMem
(float *C, float *A, float *B, const int wA,
const int wC, const int hC)
{
__shared__ float sRow[shWASize];
// 定义共享内存的大小
int blockID = blockIdx.x;
while (blockID < hC) {
int thIdx = threadIdx.x;
while (thIdx < wA) {
sRow[thIdx] = A[blockID * wA + thIdx];
//数据转移到共享内存
thIdx += blockDim.x;
}
__syncthreads();
thIdx = threadIdx.x;
while (thIdx < wC) { // wB = wC;
float sum = 0.0;
for (int i = 0; i < wA; i++) {
sum += sRow[i] * B[wC * i + thIdx];
}
C[blockID * wC + thIdx] = sum;
thIdx += blockDim.x;
}
blockID += gridDim.x;
}
}
|
需要注意的是,共享内存的大小是有限的,不同GPU的共享内存大小不一;其次,我们需要对共享内存里的值进行初始化,并且初始化后需要让block中的线程同步。关键内容如下:
while (thIdx < wA) {
sRow[thIdx] = A[blockID * wA + thIdx];
thIdx += blockDim.x;
}
__syncthreads(); |
采用了共享内存后,通过实测会发现,矩阵运算的时间不增反降。其实原因很简单,因为共享内存使用的成本高于其节约的时间。这样我们需要进一步优化,比如采用2D block 并配合共享内存。
3 二维块(2D Block) 优化运算
3.1 运算实现
2D block相比1D block,最大的差异是thread的编号idx由1维度变为了2维。在矩阵的乘法中,我们可以将矩阵拆成子矩阵,让每个block对应计算一个子矩阵。如下图所示,我们计算C=A x B,如果只获得C中某个子矩阵Cs(假设Cs的大小为M * M) , 只需要抽取A的M行数据,以及B的M列数据,进行运算。
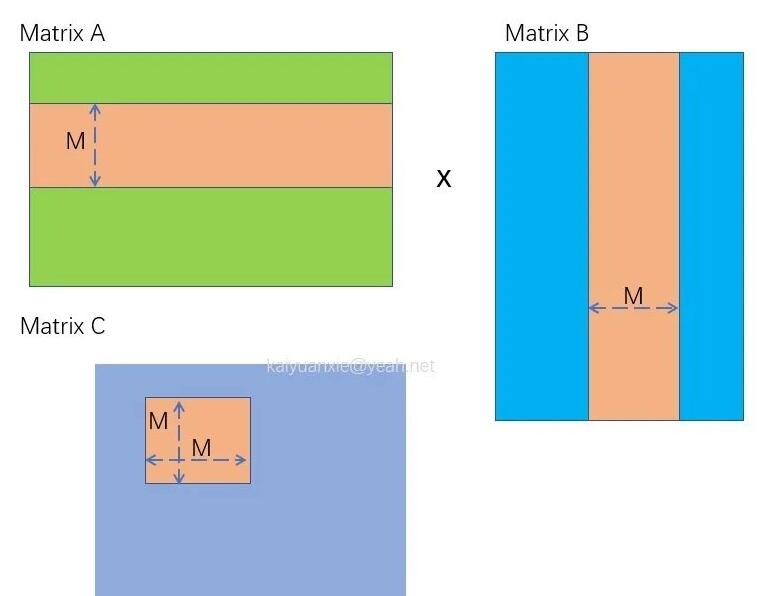
Cs矩阵的具体运算可拆解为:Cs = As0 x Bs0 + As1 x Bs2 + ... + Asm x Bsm. 如下图所示,我们用宽度为M的方块去分割数据。这样每个小矩阵的大小都是M * M。那么,为什么要进行分割运算,直接运算不是很简洁?实际上就是为了使用共享内存,减少数据的加载次数。上面运算中,例如As0 x Bs0运算由于As0与Bs0矩阵可以足够小,都能加载到共享内存中,每个数据可减少M - 1次全局内存读写。
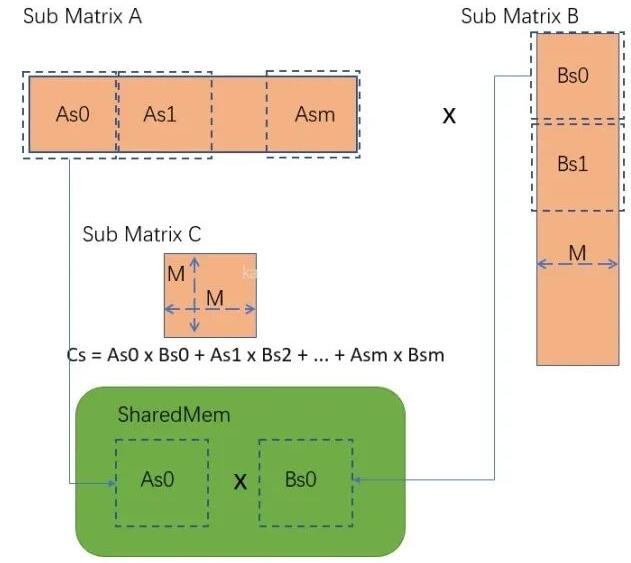
一般而言M * M设置的大小与CUDA中2D Block的大小一致,这样能够简化运算:
优化的代码关键如下:
template <int BLOCK_SIZE> __global__ void
MatMulKernel2DBlockMultiplesSize
(float *C, float *A, float *B, int wA, int wB)
{
for (int a = aBegin, b = bBegin; a <= aEnd;
a += aStep, b += bStep) {
// As与Bs 加载到共享内存中:
__shared__ float As[BLOCK_SIZE][BLOCK_SIZE]
__shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE]
//让As Bs的数据初始化,从原始数据中映射:
As[ty][tx] = A[a + wA * ty + tx];
Bs[ty][tx] = B[b + wB * ty + tx];
// Synchronize to make sure the matrices
__syncthreads();
#pragma unroll
// 子矩阵的运算数据相加
for (int k = 0; k < BLOCK_SIZE; ++k) {
Csub += As[ty][k] * Bs[k][tx];
}
__syncthreads();
}
// 最终结果让汇总:
int c = wB * BLOCK_SIZE*by+BLOCK_SIZE*bx;
C[c + wB * ty + tx] = Csub;
}
|
3.2 运算支持动态尺寸
在上述2D运算中,我们忽略一个问题,就是运算矩阵的长宽有可能不能够被Block整除,如下所示:
示例1:矩阵宽度经过M整除后,最后一个行块的宽度小于M;
示例2:矩阵的高度经过M整除后,最后一个列块的高度小于M;
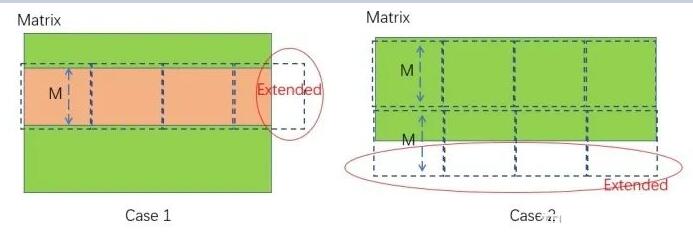
这样我们需要增加一些循环+条件判断来处理最后一个行块/最后一个列块的运算问题。
// ....
if (flag * BLOCK_SIZE + ty<wA||flag *
BLOCK_SIZE + tx < wC) {
Bs[ty][tx] = B[b + wB*ty+tx];
} else {
Bs[ty][tx] = 0.0;
}
//....
if (BLOCK_SIZE * bx + tx
< wC && BLOCK_SIZE * by + ty<hC){
{ // thread could over max.
C[wB * BLOCK_SIZE * by+BLOCK_SIZE *
bx + wB * ty + tx] = Csub;
}
|
3.3 CUBLAS函数调用
常用的矩阵运算,在CUDA的库CUBLAS中有现成的API函数。一般而言,它的运算方法比普通的优化运算要快,比如本例中的矩阵乘,可以调用cublasSgemm来运算。cublasSgemm调用非常方便。如下形式:
// ...
const float alpha = 1.0f;
const float beta = 0.0f;
cublasHandle_t handle;
checkCudaErrors(cublasCreate(&handle));
checkCudaErrors(cublasSgemm(
handle, CUBLAS_OP_N, CUBLAS_OP_N,
dimsB.x, dimsA.y,
dimsA.x, &alpha, d_B, dimsB.x, d_A,
dimsA.x, &beta, d_C, dimsB.x));
// ...
checkCudaErrors(cublasDestroy(handle));
|
但是不要过分迷信CUBLAS,毕竟它是个通用库,考虑的是通用性。对于一些特殊场景手写kernel有可能超过CUBLAS的运算。
4 代码的编译与运行
默认编译:
指定SM编译:比如A100机器,指定SMS=80
$ cd <dir>
$ make SMS='80' |
运行直接执行matMul,例如A(312,1000) * B(1000,11),指定“ MatMul_2D_KERNEL_ANY_SIZE ” 函数运行:
$ ./matMul wA=1000 hA=312 wB=11 hB=1000 algo=4
|
algo是指定某个方法运算,如果不指定,即运行所有方法。可以用help查看:
$ ./matMul help
Usage -device=n (n >= 0 for deviceID)
-wA=WidthA -hA=HeightA
(Width x Height of Matrix A)
-wB=WidthB -hB=HeightB
(Width x Height of Matrix B)
-iter=n Iteration numbers of algorithm.
Default:500
-algo=[0|1|2|3|4|5] 0: Test all,
1: MatMul_1D_KERENL,
2:MatMul_1D_KERNEL_WITH_SHARED_MEMORY,
3: MatMul_2D_KERENEL_BLOCK_MULTIPLES_SIZE,
4: MatMul_2D_KERNEL_ANY_SIZE
5: MatMul_CUBLAS_SGEMM_KERNEL
Note: Outer matrix dimensions of A&B
matrices must be equal.
|
运行效果(Test on A100):
./matMul wA=1024 hA=256 wB=128 hB=1024
NOTE: The CUDA Samples are not meant
for
performance measurements.
Results may vary when GPU Boost is enabled.
MatrixA(1024,256), MatrixB(128,1024)
==1D blocks without shared memory =
Computing result using MatrixMul1DTest
Shared Mem:
0 Warmup operation done
Performance= 883.88 GFlop/s,
Time= 0.076 msec,
Size= 67108864 Ops,
WorkgroupSize= 1024 threads/block
Checking computed result for correctness:
Result = PASS
=======1D blocks with shared memory ====
Computing result using MatrixMul1DTest
Shared Mem:
1
Warmup operation done
Performance= 227.81 GFlop/s,
Time= 0.295 msec,
Size= 67108864 Ops,
WorkgroupSize= 1024 threads/block
Checking computed result for correctness:
Result = PASS
===2D blocks with block multiples size ==
Computing result using MatMul2DTest Kernel.
Warmup operation done
Performance= 1120.85 GFlop/s,
Time= 0.060 msec,
Size= 67108864 Ops,
WorkgroupSize= 1024 threads/block
Checking computed result for correctness:
Result = PASS
=== 2D blocks with any size =====
Computing result using MatMul2DTest Kernel.
Spport any size,
e.g. wA=1000 hA=312 wB=11 hB=1000.
Warmup operation done
Performance= 1303.89 GFlop/s,
Time= 0.051 msec,
Size= 67108864 Ops,
WorkgroupSize= 1024 threads/block
Checking computed result for correctness:
Result = PASS
===CUBLAS Sgemm kernel ====
Computing result using CUBLAS Sgemmm Kernel.
Warmup operation done
Performance= 7189.46 GFlop/s,
Time= 0.009 msec,
Size= 67108864 Ops,
Checking computed result for correctness:
Result = PASS |
|
