| UML软件工程组织 | |||
| |
|||
|
|||
2008-07-18 作者:Brent Boyer 出处:IBM
程序性能一直是受到关注的问题,即使在现在这样的高性能硬件时代,也是如此。本文是分两部分的文章系列的第二篇,讨论基准测试的统计问题并提供一个框架,可以用这个框架对各种 Java™ 代码进行基准测试,包括自我包含的微基准测试和调用整个应用程序的代码等等。 本系列的 第 1 部分 解释了与 Java 代码基准测试相关联的许多问题。本文讨论另外两个领域。首先,讨论一些有助于克服基准测试中不可避免的度量偏差的统计技术。然后,介绍一个软件基准测试框架并对一系列示例使用这个框架,以说明要点。 统计如果只需执行一次执行时间度量,然后就可以用单一度量值比较不同代码的性能,那就太方便了。遗憾的是,这种方法虽然很流行,但是很不可靠。有许多因素会导致结果的偏差,所以无法信任单一度量值的精确性。在 第 1 部分 中,我提到过时钟分辨率、复杂的 JVM 行为和自动的资源回收,这些都是噪声源,它们会影响结果的精确性;这些只是能够随机或系统化地影响基准测试的众多因素的一小部分。可以采取一些措施来减轻一些因素的影响;如果有充分的理解,甚至可以执行去卷积(deconvolution)(参见 参考资料)。但是,这些补救措施都不完美,所以最终必须由您来处理偏差。惟一的方法是执行多次度量,然后用统计技术生成可靠的结果。正如 “He who refuses to do arithmetic is doomed to talk nonsense” 中指出的,忽略统计技术是很危险的(参见 参考资料)。 我在本文中只讨论解决以下这些常见性能问题所需的统计技术:
如果做多次执行时间度量,那么首先要计算的统计数据可能是一个代表典型值 的单一数字(参考资料 中的一篇 Wikipedia 文章定义了本文涉及的统计学概念)。最常用的计算方法是算术平均值,通常称为平均值 或均值,也就是所有度量值的和除以度量值的数量: meanx = Summationi=1,n(xi) / n 本文配套网站上的补充资料(参见 参考资料)讨论了除平均值之外的其他统计数据;参见其中的 Alternatives to the mean 一节。 用几个度量值的平均值来量化性能,肯定比使用单一度量值更准确,但这还不能判断哪个任务执行得更快。例如,假设任务 A 的平均执行时间是 1 毫秒,任务 B 的平均执行时间是 1.1 毫秒。能够由此得出任务 A 比任务 B 快的结论吗?如果您知道任务 A 的度量值范围是 0.9 到 1.5 毫秒,任务 B 的度量值范围是 1.09 到 1.11 毫秒,恐怕就不会下这样的结论了。因此,还需要解决度量值的跨度。 描述度量值跨度(或者说漂移)的最常用统计技术是标准偏差(standard deviation): sdx = sqrt{ Sumi=1,n( [xi - meanx]2 ) / n } 标准偏差如何量化度量值漂移?它依赖于您对度量值的概率密度函数(probability density function,PDF)的认识。您做的假设越强,得到的结论就越好。本文补充资料的 Relating standard deviation to measurement scatter 一节详细解释了这个概念并得出以下结论:在基准测试上下文中,合理的经验规则是至少 95% 的度量值应该落在平均值的三倍标准偏差的范围内。 那么,如何用平均值和标准偏差判断两个任务中哪一个更快呢?根据上面的经验规则,最简单的情况是两个任务的平均值之差超过了三倍标准偏差(选用两个标准偏差中较大者)。在这种情况下,平均值小的任务显然在大多数时候都更快,见图 1: 图 1. 平均值之差超过三倍标准偏差,这表示可以明确分辨出性能差异
不幸的是,两个任务的重叠部分越大,判断就越困难(例如,如果平均值只相差一个标准偏差),见图 2: 图 2. 平均值之差小于三倍标准偏差,性能数据出现重叠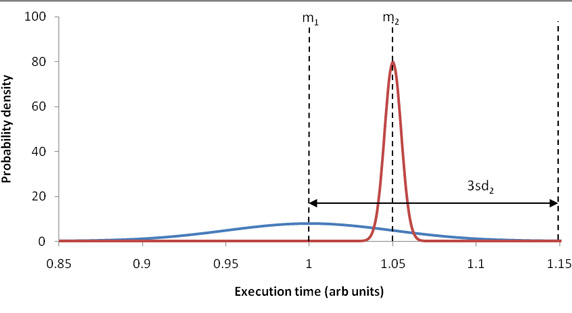
我们可以这样做:根据平均值判断两个任务的性能水平,但是要注意数据的重叠程度并相应地指出结论的可靠程度。 要解决的另一个问题是,这些平均值和标准偏差统计值本身的可靠性如何。显然,这些数据是从度量值计算出来的,所以另一组度量值很可能产生不同的统计值。现在,假设度量过程是有效的。(注意:不可能测量出 “真实的” 标准偏差。补充资料的 Standard deviation measurement issues 一节解释了这个问题)。那么,如果重复执行度量过程,平均值和标准偏差会有多大变化?另一组度量值会产生明显不同的结果吗? 要回答这些问题,最明显的方法是为统计数据构造置信区间(confidence interval)。置信区间并不是统计数据的单一计算值(估值点[point estimate]),而是一个估值范围。与这个范围相关联的概率 p 称为置信水平(confidence level)。在大多数情况下,设 p 为 95%,这个值在置信区间比较期间保持不变。置信区间的意义很直观,因为它们的大小表示可靠性:窄的区间表示统计数据比较精确,宽的区间表示统计数据不太确定。例如,如果任务 A 的平均执行时间的置信区间是 [1, 1.1] 毫秒,任务 B 是 [0.998, 0.999] 毫秒,那么 B 的平均值就比 A 可靠性高,还可以确认它的值比 A 小(在置信水平上)。补充资料的 Confidence intervals 一节详细讨论了这个问题。 在以前,只能针对一些常见的 PDF(比如 Gaussian)和简单的统计数据(比如平均值)计算置信区间。但是,在 20 世纪 70 年代晚期,开发出了一种称为 bootstrapping 的技术。这是一种用来产生置信区间的通用技术。它适用于任何统计数据,而不只是平均值这样的简单数据。另外,非参数化形式的 bootstrapping 不需要对底层 PDF 做任何假设。它不会产生非物理结果(例如,置信区间的下限为负的执行时间);与对 PDF 做出错误假设的情况(比如假设是 Gaussian)相比,bootstrapping 产生更窄更精确的置信区间。对 bootstrapping 的详细讨论超出了本文的范围,但是下面讨论的框架包含一个 Bootstrap 类,这个类会执行 bootstrapping 计算;更多信息参见它的 Javadoc 和源代码(参见 参考资料)。 总之,您必须:
框架简介到目前为止,我已经讨论了 Java 代码基准测试的一般原理。现在要介绍一个简便的基准测试框架,这个框架解决了前面提到的许多问题。 请从本文的配套网站下载项目的 ZIP 文件(参见 参考资料)。这个 ZIP 文件包含源代码和二进制文件,以及一个简单的构建环境。它包含本文中的所有代码清单。把它的内容解压到任意目录中。在顶层目录中的 readMe.txt 文件中可以找到更多信息。 在这个框架中,主要的类是 Benchmark。大多数用户只需要使用这个类;其他东西都是起辅助的。API 的基本用法很简单:把要进行基准测试的代码提供给一个 Benchmark 构造函数。然后,就会完全自动地执行基准测试过程。通常只有一个后续步骤,即生成 结果报告。 显然,必须有一些代码,希望对其执行时间进行基准测试。惟一的限制是,代码应该包含在 Callable 或 Runnable 中。除此之外,目标代码可以是能够用 Java 语言表达的任何代码,包括自我包含的微基准测试和调用整个应用程序的代码等等。 把任务编写为 Callable 常常更方便。Callable.call 允许抛出受检查的 Exception,而 Runnable.run 要求实现 Exception 处理。另外,正如第 1 部分的 消除死代码 一节指出的,与 Runnable 相比,Callable 更容易防止 DCE。把任务编写为 Runnable 的优点是,这可以尽可能降低创建对象和垃圾收集的开销;更多信息参见补充资料的 Task code: Callable versus Runnable 一节。 要获得基准测试结果报告,最容易的方法是调用 Benchmark.toString 方法。这个方法产生一个单行的汇总报告,其中只包含最重要的结果和 警告。通过调用 Benchmark.toStringFull 方法,可以获得详细的多行报告,其中包含所有结果和完整的解释。除此之外,还可以调用 Benchmark 的各种访问函数来生成定制的报告。 Benchmark 会尝试诊断一些常见的问题,如果探测到这些问题,就会在 结果报告 中提出警告。警告包括:
下面用清单 1 中的代码片段演示前面讨论的要点: 清单 1. 对计算第 35 个 Fibonacci 数的过程进行基准测试
在清单 1 中,main 把要测试的代码定义为 Callable,然后提供给 Benchmark 构造函数。Benchmark 构造函数多次执行一个任务,首先确保完成 代码预热,然后收集执行时间统计数据。构造函数返回之后,它所在的代码上下文(即 println 的内部)隐式地调用新的 Benchmark 实例的 toString 方法,这会报告基准测试的汇总统计数据。通常,Benchmark 的使用就这么简单。 在我的配置上,获得了以下结果:
下面解释这些结果:
数据结构访问时间为了更好地说明基准测试问题以及如何使用 Benchmark 解决它们,下面对几种常用数据结构的访问时间进行基准测试。 只度量一种数据结构的访问时间是一种真正的微基准测试。的确,微基准测试有许多问题。(例如,它们对于考察完整应用程序的性能意义不大)。但是,这是情有可原的,因为它们很难得到精确的结果。这种度量涉及许多有意思的问题(比如缓存的影响),所以适合作为示例。 请考虑清单 2 中的代码,这段代码对数组访问时间进行基准测试(针对其他数据结构的代码是相似的): 清单 2. 数组访问基准测试代码
在理想情况下,这段代码仅仅访问 integers 数组。但是,为了方便地访问 integers 的所有元素,我使用了一个循环,这给基准测试带来了寄生循环开销。注意,我使用的是一个老式的显式 int 循环,而不是更方便的 for (int i : integers) 改进型 for 循环,因为它的速度快一点儿(参见 参考资料)。这里使用的循环应该算是一个缺陷,但是影响不大,因为所有即时(JIT)编译器都会执行循环展开,这会降低循环的影响。 但最为重要的是防止 DCE 所需的代码。首先,选用 Runnable 作为任务类,因为这可以尽可能降低创建对象和垃圾收集的开销,这对于这样的微基准测试很重要。第二,既然这个任务类是 Runnable,为了防止 DCE,必须把数组访问的结果赋值给 state 字段(以及覆盖的 toString 方法中需要使用的 state)。第三,对数组访问和以前的 state 值执行位 XOR 计算,以确保执行每个 访问。(如果只执行 state = integers[i],聪明的编译器可能会发现可以跳过整个循环,直接执行 state = integers[integers.length - 1])。这四个额外操作(字段读、把 Integer 自动转换为 int、位 XOR、字段写)是不可避免的开销,这些开销会歪曲基准测试的结果:实际上度量的不只是数组访问时间。所有其他数据结构基准测试也有相似的问题,但是对于访问时间相当长的数据结构,这种影响可以忽略。 图 3 和图 4 给出在我常用的桌面配置上对两个不同大小的 integers 的访问时间结果: 图 3. 数据结构访问时间(1024 个元素)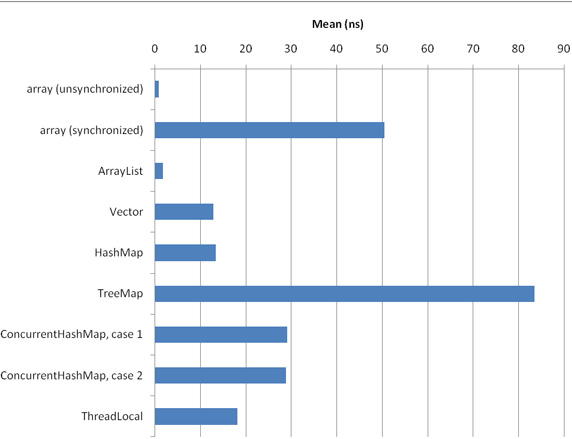
图 4. 数据结构访问时间(1024 × 1024 个元素) 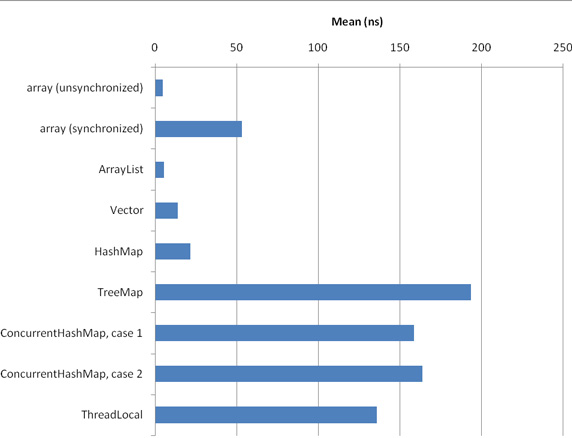
下面对结果做一些说明:
这些结果可能符合您的预期:不同步的数组访问是最快的数据结构。ArrayList 的速度处于第二位,几乎与原始数组一样快。(可能是因为服务器 JVM 对底层数组的直接访问进行了出色的内联处理)。它比同步的相似 Vector 快得多。更慢一点儿的数据结构是 HashMap,然后是 ThreadLocal(这基本上是一个以当前线程作为键的特殊散列表)。实际上,在这些测试中,HashMap 几乎与 Vector 一样快,这是因为使用 Integer 作为键,而且 hashCode 的实现非常快(仅仅返回 int 值)。接下来是 ConcurrentHashMap,最后是最慢的结构 TreeMap。 我还在另一台完全不同的机器上执行了完全相同的基准测试(SPARC-Enterprise-T5220,运行频率 1.167GHz,32GB RAM,使用 SunOS asm03 5.10;使用的 JVM 版本和设置与我的桌面机相同,但是把 Benchmark 配置为度量 CPU 时间而不是流逝时间,因为测试都是单线程的,而 Solaris 支持单线程),但是这里没有给出结果。各种结构的相对结果与上面的结果相同。 在上面的结果中,惟一重大的不正常情况是同步的数组访问时间:我原来认为它们应该与 Vector 差不多,但是却慢了三倍。我猜测其原因可能是一些与锁相关的优化(比如锁省略或锁 biasing)无法进行(参见 参考资料)。在 Azul 的 JVM 中没有出现这种异常情况,而这种 JVM 使用定制的锁优化,这似乎证明了我的猜测是正确的。 另一个比较小的异常情况是,ConcurrentHashMap 的第一种情况只在使用 1024 × 1024 个元素时比第二种情况快,在使用 1024 个元素时实际上略微慢一点儿。这个异常情况可能是由不同数量的表片段的内存放置效应造成的。这种效应在 T5220 机器上不存在(无论使用多少个元素,第一种情况总是比第二种情况快一点儿)。 另一个不正常情况是 HashMap 比 ConcurrentHashMap 快。这两种情况的代码与 清单 2 相似,但是把 state ^= integers[i] 替换为 state ^= map.get(integers[i])。integers 的元素按顺序出现(integers[i].intValue() == i)并以相同的次序作为键使用。这说明 HashMap 中的散列预处理函数的顺序缓存位置比 ConcurrentHashMap 更好(因为 ConcurrentHashMap 需要更好的高位分布)。 这就引出了一个有意思的问题:上面给出的结果在多大程度上依赖于按顺序遍历 integers?内存位置效应是否对于某些数据结构更有利?为了回答这些问题,我重新运行这些基准测试,但是这一次随机选择 integers 的元素,而不是顺序选择。(我用一个软件线性反馈偏移寄存器来生成伪随机值;参见 参考资料。这会给每次数据结构访问增加 3 纳秒的开销)。对于 1024 × 1024 个元素的 integers,基准测试结果见图 5: 图 5. 数据结构访问时间(1024 × 1024 个元素,随机访问)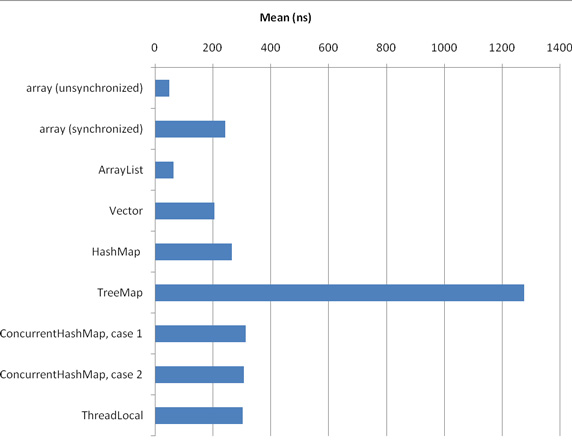
与 图 4 相比,HashMap 现在的性能与 ConcurrentHashMap 差不多相同(这符合预期)。TreeMap 的随机访问性能非常差。数组和 ArrayList 数据结构仍然是最好的,但是它们的相对性能变差了(与顺序访问相比,它们的随机访问性能差了大约 10 倍,而 ConcurrentHashMap 的随机访问性能只差了大约 2 倍)。 另一个要点:图 3、图 4 和图 5 显示的是个别 访问时间。例如,在 图 3 中,可以看到访问 TreeMap 中一个元素所用的时间是 80 纳秒多一点。但是,所有任务都与 清单 2 相似;也就是说,每个任务在内部都执行多次数据访问(即循环遍历 integers 的每个元素)。那么,如何从包含几个相同 操作的任务中提取出个别操作的统计数据呢? 可以以 清单 2 为基础,编写出处理这种任务的代码。可以使用与清单 3 相似的代码: 清单 3. 处理包含多个操作的任务的代码
在清单 3 中,使用了 Benchmark 构造函数的两参数版本。第二个参数(在清单 3 中用粗体显示)指定任务包含的相同操作 的数量,在这里是 m = integers.length。更多信息参见补充资料的 Block statistics versus action statistics 一节。 优化投资组合计算在本文中,到目前为止只考虑了微基准测试。但是,度量真实应用程序的性能才是基准测试真正的用途。 证券投资者可能感兴趣的一个示例是 Markowitz 均值-方差投资组合优化,金融顾问使用这种标准技术建立具有出色的风险/收益比的投资组合(参见 参考资料)。 WebCab Components 公司提供了一个执行这些计算的 Java 库(参见 参考资料)。清单 4 中的代码对 Portfolio v5.0(J2SE Edition)库在求解有效边界(efficient frontier) 时的性能进行基准测试(参见 参考资料): 清单 4. 投资组合优化基准测试代码
因为本文讨论的是基准测试,而不是投资组合理论,所以我们不用理会 EfTask 内部类的代码。(简单地说,EfTask 获取资产历史回报数据,由此计算预期的回报和协方差,求出有效边界上的 50 个点,然后返回具有最大 Sharpe 比率的那个点;参见 参考资料。这个最佳 Sharpe 比率表示最佳投资组合对于特定资产集的效果如何,由此在风险调整的基础上识别出最佳回报。细节参见示例代码包中的相关源代码文件)。 这段代码的目的是,判断执行时间和投资组合质量随资产数量变化的趋势,这对于投资组合优化可能很有帮助。清单 4 中的 n 循环完成这个判断。 这个基准测试有几个难点。首先,计算花费的时间很长,尤其是在涉及大量资产时。因此,我避免使用 new Benchmark(task) 这样的简单代码(它在默认情况下执行 60 次度量)。而是创建一个定制的 Benchmark.Params 实例,它指定应该只执行一次度量。(它还指定应该进行 CPU 时间度量,而不是默认的流逝时间度量,这只是为了演示 CPU 时间度量。因为 WebCab Components 库在这个上下文中没有创建线程,所以可以这样做)。但是,在执行这一次度量值基准测试之前,i 循环会执行几次基准测试,让 JVM 能够完全完成代码优化。 第二,通常的 结果报告 对于这个基准测试不够精确,所以我生成一个定制的报告,它应该只提供以制表符分隔的数字,这样就很容易复制到电子表格中,供以后绘图时使用。因为只进行一次度量,所以用 Benchmark 的 getFirst 方法获取执行时间。给定资产集的最大 Sharpe 比率是 Callable 任务的返回值。可以通过 Benchmark 的 getCallResult 方法获得这个值。 另外,我希望以图形方式显示结果的漂移,所以对于给定的资产集,内部的 j 循环执行每个基准测试 20 次。这样的话,对于每个资产数量,在下图中生成 20 个点。(在某些情况下,一些点重叠在一起,所以看起来只有几个点)。 看一下结果。我使用的资产是当前 OEX(S&P 100)索引中的股票。使用过去 3 年(2005 年 1 月 1 日到 2007 年 12 月 31 日)的每周资本收益作为历史回报数据;忽略分红(如果包含分红,会略微提高 Sharpe 比率)。 图 6 是执行时间随资产数量变化的图形: 图 6. 投资组合优化执行时间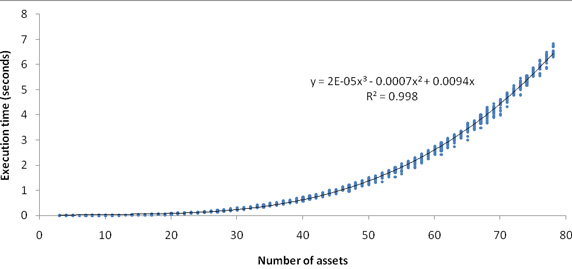
所以,执行时间随资产数量的三次方增长。这些度量值的漂移是真实的,不是基准测试错误:投资组合优化的执行时间依赖于考虑的资产类型。尤其是,某些协方差类型需要非常仔细(步长很小)的数字计算,这会影响执行时间。 图 7 是投资组合质量(最大 Sharpe 比率)随资产数量变化的图形: 图 7. 投资组合质量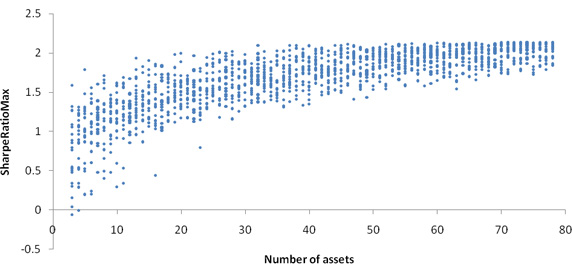
最大 Sharpe 比率最初上升,但是不久就在大约 15 到 20 种资产处停止增加。在此之后,随着资产数量的增加,惟一的效果是最大值的范围逐渐收窄。这个效果也是真实的:这是因为随着资产数量的增加,投资组合中包含所有 “热门” 资产(在最佳投资组合中占据优势地位的资产)的可能性逐渐接近 100%。更多信息参见补充资料的 Portfolio optimization 一节。 最后几点提示微基准测试应该反映真实用例。例如,我选择测试数据结构的访问时间,这是因为在设计 JDK 集合时假设典型的应用程序包含 85% 的读/遍历、14% 的添加/更新和 1% 的删除操作。但是,如果各种操作的比例发生变化,相对性能就会有很大变化。另一个危险因素是复杂的类层次结构:微基准测试常常使用简单的类层次结构,但是在复杂的类层次结构中方法调用开销会显著增加(参见 参考资料),所以精确的微基准测试必须反映真实应用程序中的情况。 要确保基准测试结果是相关的。提示:针对 StringBuffer 和 StringBuilder 的微基准测试不可能说明 Web 服务器的性能怎么样;更高级的体系结构选择的影响可能显著得多,而这些选择不适合进行微基准测试。(但是,在几乎所有代码中都应该使用 ArrayList/HashMap/StringBuilder,而不是老式的 Vector/Hashtable/StringBuffer)。 最好不要仅仅依赖于微基准测试的结果。例如,如果希望测试一种新算法的性能,那么不但要在基准测试环境中进行度量,还应该在真实应用程序场景中度量,了解它是否会产生显著的性能差异。 显然,只有在测试了合理的计算机和配置样本之后,才能做出具有普遍意义的性能结论。不幸的是,常常只在开发机器上执行基准测试,并假设在所有机器上都能够得出相同的结论。如果希望彻底测试,就需要多种硬件,甚至不同的 JVM(参见 参考资料)。 不要忽视剖析。应该用能够找到的各种剖析工具运行基准测试,从而确认其行为符合预期(例如,大多数执行时间应该花在您认为的关键方法上)。这还可以确认 DCE 没有歪曲测试结果。 最后,要想得出正确的性能结论,就必须了解低层的操作执行方式。例如,如果希望了解 Java 语言的正弦实现(Math.sin)是否比 C 的实现快,您可能会发现在 x86 硬件上 Java 的正弦实现慢得多。这是因为 Java 避免使用快速但不精确的 x86 硬件辅助指令。不了解这个原理的人可能认为 C 比 Java 快得多,而实际情况是一个专用(但不精确)的硬件指令比一个精确的软件计算快。 结束语基准测试常常需要执行许多次度量,并使用统计技术解释结果。本文提供的基准测试框架支持这些特性并解决了许多其他问题。无论您是使用这个框架,还是按照本系列提供的信息创建自己的框架,都可以更好地执行基准测试,确保 Java 代码能够高效地执行。 参考资料学习
|
组织简介 | 联系我们 | Copyright 2002 ® UML软件工程组织 京ICP备10020922号 京公海网安备110108001071号 |