大多数开发人员认为使用测试驱动开发（TDD）最有用的部分是测试。但是，正确地完成开发后，TDD 将改进代码的整体设计。演化架构与紧急设计 系列的这一期文章将介绍一个进一步扩展的示例，演示如何根据测试中显现的关注点进行设计。测试只是 TDD 的次要部分；关键在于它如何优化代码。

常见的一种敏捷开发实践就是 TDD。TDD 是一种编写软件的模式，它使用测试帮助您了解需求阶段的最后步骤。先写测试，再编写代码，这样可以巩固您对代码所需执行的操作的理解。

大多数开发人员认为 TDD 带来的主要好处是最终得到的综合单元测试集。但是，如果正确执行的话，TDD 可以改进代码的整体设计，因为它将决策推迟到最后责任时刻（last responsible moment）。由于您没有预先做出任何设计决定，因此它让您随时可以采用更好的设计选择或者重构为更好的设计。本文将介绍一个示例，用于演示根据单元测试的结果进行设计的强大之处。

TDD 工作流程

测试驱动开发 术语中的关键词是驱动，表示测试将驱动开发流程。图 1 显示了 TDD 工作流程：

图 1 中的工作流程是：

1. 编写一个失败的测试。
2. 编写代码以使测试通过。
3. 重复第 1 步和第 2 步。
4. 在此过程中积极地重构。
5. 当您无法再想到任何测试时，那么就必须做决策了。

TDD 与先开发后测试的比较

测试驱动 开发强调首先进行测试。只有在编写了测试（并失败）后，您才可以编写测试中的代码。许多开发人员使用称为后测试开发（test-after development，TAD）的各种测试，您将首先编写代码，然后编写单元测试。在这种情况下，您仍然进行了测试，但是没有涉及到 TDD 的紧急设计方面。您可以很轻松地编写一些非常恶劣的代码，然后费劲脑筋地想办法测试。通过先编写代码，您在代码中嵌入了有关代码如何工作的想法，然后测试这些代码。TDD 要求您反过来做：先编写测试，并让它来提示如何编写可以让测试通过的代码。为了演示这个重要区别，我将着手实现一个扩展示例。

完全数

要展示 TDD 的设计优点，我需要用到一个待解决的问题。在 Kent Beck 的 Test Driven Development 一书中（请参阅 参考资料），他使用货币作为示例 — 非常优秀的 TDD 例子，但是有点过分简单。真正的挑战是找到这样一个示例，该示例本身并没有复杂到让您对问题束手无策，但是它的复杂度足以展示真正的价值。

为此，我选择了完全数。对于不熟悉数学知识的人，此概念可追溯到 Euclid 之前（他完成了导出完全数的早期验证之一）。完全数指其真因子相加等于数字本身的数字。例如，6 是一个完全数，因为 6 的因子（不包括 6 本身）是 1、2 和 3，而 1 + 2 + 3 = 6。更规则的完全数定义是因子（不包括该数字本身）之和等于该数字的数字。在我的示例中，计算结果是 1 + 2 + 3 +6 - 6 = 6。

这就是要处理的问题域：创建一个完全数查找程序。我将用两种不同的方法实现此解决方案。首先，我将打消想要执行 TDD 的念头并且只是编写解决方案，然后为它编写测试。然后，我将设计出 TDD 版本的解决方案，以便可以比较和对照两种方法。

对于本例，我用 Java 语言（版本 5 或更高版本，因为我将在测试中使用注释）、JUnit 4.x（最新版本）和来自 Google 代码的 Hamcrest 匹配器（请参阅 参考资料）实现一个完全数查找程序。Hamcrest 匹配器将在标准的 JUnit 匹配器顶部提供一个人本接口（humane interface）语法糖。例如，不必编写 assertEquals(expected, actual)，您可以编写 assertEquals(actual, is(expected))，这段代码读起来更像是一个句子。JUnit 4.x 附带了 Hamcrest 匹配器（这些匹配器只是静态导入）；如果仍然要使用 JUnit 3.x，您可以下载一个兼容版本。

后测试开发

清单 1 显示了第一个版本的 PerfectNumberFinder：

				
public class PerfectNumberFinder1 {
    public static boolean isPerfect(int number) {
        // get factors
        List<Integer> factors = new ArrayList<Integer>();
        factors.add(1);
        factors.add(number);
        for (int i = 2; i < number; i++)
            if (number % i == 0)
                factors.add(i);

        // sum factors
        int sum = 0;
        for (int n : factors)
            sum += n;

        // decide if it's perfect
        return sum - number == number;
    }
}

这并不是特别好的代码，但是它完成了工作。首先把所有因子创建为一张动态列表（ArrayList）。我把 1 和目标数字添加到列表中（我在遵守上面给出的公式，并且所有因子列表都包括 1 和该数字本身）。然后，我迭代可能的因子直到该数字本身，逐个检查以查看它是不是一个因子。如果是，我将把它添加到列表中。接下来，我将把所有因子加起来，并最终编写上面所示的公式的 Java 版本以确定是否为完全数。

现在，我需要一个后测试的单元测试以确定它是否可以工作。我至少需要两个测试：一个测试用于查看是否正确报告了完全数，另一个测试用于检查我没有得到误判断（false positives）。单元测试位于清单 2 中：

				
public class PerfectNumberFinderTest {
    private static Integer[] PERFECT_NUMS = {6, 28, 496, 8128, 33550336};

    @Test public void test_perfection() {
        for (int i : PERFECT_NUMS)
            assertTrue(PerfectNumberFinder1.isPerfect(i));
    }

    @Test public void test_non_perfection() {
        List<Integer>expected = new ArrayList<Integer>(
                Arrays.asList(PERFECT_NUMS));
        for (int i = 2; i < 100000; i++) {
            if (expected.contains(i))
                assertTrue(PerfectNumberFinder1.isPerfect(i));
            else
                assertFalse(PerfectNumberFinder1.isPerfect(i));
        }
    }

    @Test public void test_perfection_for_2nd_version() {
        for (int i : PERFECT_NUMS)
            assertTrue(PerfectNumberFinder2.isPerfect(i));
    }

    @Test public void test_non_perfection_for_2nd_version() {
        List<Integer> expected = new ArrayList<Integer>(Arrays.asList(PERFECT_NUMS));
        for (int i = 2; i < 100000; i++) {
            if (expected.contains(i))
                assertTrue(PerfectNumberFinder2.isPerfect(i));
            else
                assertFalse(PerfectNumberFinder2.isPerfect(i));
        }
        assertTrue(PerfectNumberFinder2.isPerfect(PERFECT_NUMS[4]));
    }
}

这段代码正确地报告了完全数，但是由于反向测试的原因，代码运行得非常慢，因为我需要检查大量数字。单元测试会引发性能问题，这使得我重新审视代码以查看是否可以进行一些改进。目前，我把循环集中在数字本身以获得因子。但是我必须这样做吗？如果我可以成对获得因子的话就不需要。所有因子都是成对的（例如，如果目标数字为 28，当我找到因子 2 时，我也可以获得 14）。如果我可以成对获得因子，那么我只需要循环到该数字的平方根。为此，我改进了算法并将代码重构为清单 3：

				
public class PerfectNumberFinder2 {
    public static boolean isPerfect(int number) {
        // get factors
        List<Integer> factors = new ArrayList<Integer>();
        factors.add(1);
        factors.add(number);
        for (int i = 2; i <= sqrt(number); i++)
            if (number % i == 0) {
                factors.add(i);
            }

        // sum factors
        int sum = 0;
        for (int n : factors)
            sum += n;

        // decide if it's perfect
        return sum - number == number;
    }
}

这段代码运行的时间十分合理，但是几个测试断言都失败了。结果是当您成对地获得数字时，您在到达整数平方根时将意外地获得两次数字。例如，对于数字 16，平方根是 4，该数字将被意外地添加到列表中两次。通过创建一个处理这种情况的保护条件可以轻松地解决此问题，如清单 4 所示：

				
for (int i = 2; i <= sqrt(number); i++)
    if (number % i == 0) {
        factors.add(i);
        if (number / i !=  i)
            factors.add(number / i);
    }

现在我有了后测试版本的完全数查找程序。它可以正常工作，但是一些设计问题也显现出来。首先，我使用了注释来描绘代码的各个部分。这永远是代码的一部分：希望重构为自己的方法。我刚添加的新内容可能需要使用注释说明保护条件的用途，但是我现在不管这一点。最大的问题在于其长度。我的 Java 项目的经验表明，任何方法永远不能超过 10 行代码。如果方法行数超过这个数，它几乎肯定不止做一件事，而这是不应该的。此方法明显地违背了这条经验，因此我将进行另外一种尝试，这次使用 TDD。

通过 TDD 进行紧急设计

编写 TDD 的信条是：“可以为其编写测试的最简单内容是什么？” 在本例中，是否为 “是否是一个完全数？” 不 — 这个答案过于宽泛。我必须分解问题并回想 “完全数” 的含义。我可以轻松地举出查找完全数必需的几个步骤：

• 我需要所求数字的因子。
• 我需要确定某个数字是不是因子。
• 我需要把因子加起来。

想一想最简单的事情是什么，此列表中的哪一条看上去最简单？我认为是确定数字是不是另一个数字的因子，因此这是我的第一个测试，如清单 5 所示：

				
public class Classifier1Test {

    @Test public void is_1_a_factor_of_10() {
        assertTrue(Classifier1.isFactor(1, 10));
    }
}

这项简单测试琐碎得有些愚蠢，这就是我需要的。要编译此测试，您必须有名为 Classifier1 的类，并且它有 isFactor() 方法。因此我必须先创建类的骨架结构，然后才可以得到表示测试结果不正确的红条。编写极度琐碎的单元测试可以先把结构准备就绪，然后才需要开始通过所有有意义的方法考虑问题域。我希望一次只考虑一件事，而且这使得我可以处理骨架结构，而无需担心正在解决的问题的细微差别。一旦我可以编译这段代码并且得到表示测试失败的红条，我就准备好编写代码，如清单 6 所示：

				
public class Classifier1 {
    public static boolean isFactor(int factor, int number) {
        return number % factor == 0;
    }
}

好的，这段代码很好而且很简单，并且它可以完成工作。现在我可以转到下一项最简单的任务：获得数字的因子列表。测试显示在清单 7 中：

				
@Test public void factors_for() {
    int[] expected = new int[] {1};
    assertThat(Classifier1.factorsFor(1), is(expected));
}

清单 7 显示了我为获得因子编写的最简单测试，因此现在我可以编写使此测试通过的最简单代码（并在以后将其重构以使其更复杂）。下一个方法显示在清单 8 中：

				
public static int[] factorsFor(int number) {
    return new int[] {number};
}

虽然这个方法可以工作，但是它使我完全停了下来。将 isFactor() 方法变成静态方法似乎是个好主意，因为它只不过根据其输入返回一些内容。但是，现在我也已经使 factorsFor() 方法成为了静态方法，意味着我必须将名为 number 的参数传递给两个方法。这段代码将变得非常过程化，这是过分使用静态的副作用。为了解决此问题，我将重构已有的两个方法，这很简单，因为到目前为止我只有很少的代码。重构后的 Classifier 类显示在清单 9 中：

				
public class Classifier2 {
    private int _number;

    public Classifier2(int number) {
        _number = number;
    }

    public boolean isFactor(int factor) {
        return _number % factor == 0;
    }
}

我把数字变成是 Classifier2 类中的成员变量，这将允许我避免将其作为参数传递给一大堆静态方法。

我的分解列表中的下一件事表明我需要找到数字的因子。因此，我的下一个测试应当检查这一点（如清单 10 中所示）：

				
@Test public void factors_for_6() {
    int[] expected = new int[] {1, 2, 3, 6};
    Classifier2 c = new Classifier2(6);
    assertThat(c.getFactors(), is(expected));
}

现在，我将试着实现返回给定参数的因子数组的方法，如清单 11 中所示：

				
public int[] getFactors() {
    List<Integer> factors = new ArrayList<Integer>();
    factors.add(1);
    factors.add(_number);
    for (int i = 2; i < _number; i++) {
        if (isFactor(i))
            factors.add(i);
    }
    int[] intListOfFactors = new int[factors.size()];
    int i = 0;
    for (Integer f : factors)
        intListOfFactors[i++] = f.intValue();
    return intListOfFactors;
}

这段代码允许测试通过，但是再考虑一下，它十分糟糕！在使用测试研究实现代码的方法时有时会出现这种情况。这段代码中哪些部分非常糟糕？首先，它非常长而且复杂，并且它也有 “不止一件事” 的问题。我的本能指引我返回 int[]，但是它给底部的代码增加了很多复杂度而没有给我带来任何好处。开始过多地考虑怎样做才能使将来可能调用此方法的方法更方便，将令您遭遇危险的处境。您需要一个非常有说服力的理由才能在此接合点添加复杂的内容，而我还没有那样的理由。查看这段代码，我发现 factors 也应当作为类的内部状态而存在，使我可以分解该方法的功能。

测试显现的有益特性之一是真正内聚的方法。Kent Beck 在十分有影响力的 Smalltalk Best Practice Patterns 一书中提到了这一点（请参阅 参考资料）。在该书中，Kent 定义了一种名为组合方法（composed method）的模式。组合方法模式将定义三条主要语句：

• 把程序划分为多个可执行一项可识别任务的方法。
• 把方法中的所有操作保持在同一个抽象级别
• 这将自然而然地得到拥有许多小方法的程序，每个小方法都只有几行代码。

组合方法是 TDD 提倡的有益设计特性之一，而我已经在 清单 11 的 getFactors() 方法中明显违反了这种模式。我可以通过执行以下步骤来修正：

1. 将 factors 提升为内部状态。
2. 将 factors 的初始化代码移到构造函数中。
3. 去掉对 int[] 代码的转换，等到它变得有益时再处理它。
4. 添加 addFactors() 的另一项测试。

第四步非常微妙但是很重要。编写出这个有缺陷的代码版本揭示出分解的第一步并不完整。隐藏在这个长方法中间的 addFactors() 代码行是可测试的行为。它是如此地微不足道，以至于在第一次查看问题时我都没有注意到它，但是现在我看到了。这是经常出现的情况。一个测试可以指引您进一步将问题分解为越来越小的块，每个块都是可以测试的。

我将暂停处理 getFactors() 的比较大的问题，而处理我新遇到的小问题。因此，我的下一个测试是 addFactors()，如清单 12 中所示：

				
@Test public void add_factors() {
    Classifier3 c = new Classifier3(6);
    c.addFactor(2);
    c.addFactor(3);
    assertThat(c.getFactors(), is(Arrays.asList(1, 2, 3, 6)));
}

清单 13 所示的测试中的代码本身十分简单：

				
public void addFactor(int factor) {
    _factors.add(factor);
}

我运行我的单元测试，充满信心地认为我会看到表示测试成功的绿条，但是却失败了！这样一个简单的测试怎么会失败？根本原因显示在图 2 中：

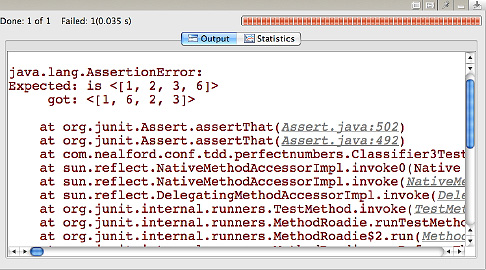
我期望看到的列表有 1, 2, 3, 6 几个值，而实际返回的是 1, 6, 2, 3。那是因为我将代码改为在构造函数中添加 1 和数字本身。这个问题的一种解决方案是，始终在假定应先添加 1 和该数字的情况下编写期望的代码。但是这是正确的 解决方案吗？不是。问题更为基础。因子是不是一个数字列表？不是，它们是一个数字集合。我的第一个（错误）假定导致我使用一列整数作为因子，但是这是个糟糕的抽象。通过将我的代码重构为使用集合而非列表，我不但解决了这个问题，而且优化了整个解决方案，因为我现在使用的是更精确的抽象。

如果在让代码影响您的判断力之前编写测试，这正是测试可以揭露的有缺陷的思维方式。现在，由于这项简单的测试，我编写的代码的整体设计更好了，因为我已经发现了更合适的抽象。

结束语

到目前为止，我以处理完全数为背景讨论了紧急设计。特别是，注意第一版的解决方案（后测试版本）对数据类型做出了同样有缺陷的假设。“后测试” 将测试代码的粗糙功能，而非各个部分。TDD 将测试构成粗糙功能的构建块，在测试过程中揭露更多信息。

在下一期文章中，我将继续讨论完全数问题，演示在执行测试时形成的各种设计的更多示例。在我完成 TDD 版本时，我将比较一下两个代码库。我还将解答其他某些棘手的 TDD 设计问题，例如是否测试及何时测试私有方法。

参考资料

• Hamcrest 匹配器：一个匹配器对象库，允许您通过声明方式定义 “匹配” 以供在其他框架中使用。
• Test-Driven Development（Kent Beck，Addison-Wesley，2003）：Beck，极限编程的创始人，将使用基于货币的示例来解读 TDD。
• Smalltalk Best Practice Patterns（Kent Beck，Prentice Hall，1996）：了解组合方法 模式的更多信息。
• The Productive Programmer（Neal Ford，O'Reilly Media，2008）：Neal Ford 的新书的 “Test Driven Development” 一章中有本文示例的较长版本。。
• “Emergent Optimization in Test Driven Design”（Michael Feathers）：测试如何帮助避免过早优化。
• 浏览 技术书店 查找关于这些主题和其他技术主题的书籍。
• developerWorks Java 技术专区：查找数以百计的关于 Java 编程的文章。

• JUnit：下载 JUnit。

• 查阅 developerWorks blog 并加入 developerWorks 社区。