| 编辑推荐: |
| 本文来自于微信公众号:依阳实业,
本文针对测试定形相变材料热性能的ASTM C1784动态热流计法(DHFM),采用基于Modelica语言的SimulationX软件,建立测试热焓和比热容的模拟仿真模型,对测试方法开展更深入的研究。 |
|
1. 概述
随着建筑节能以及能量存储的需要,相变材料技术得到了飞速发展,出现了各种新型的定形相变复合材料,而定形相变复合材料的热焓、比热和导热系数等是相变材料设计、研制和生产过程中的重要物理性能参数。为了保证新型定形相变材料的热物理性能测试的准确性,ASTM
在2013年制定了一个新的测试标准:ASTM C1784-13“采用热流计装置测量相变材料及其产品储热特性的标准测试方法”,并在2014年颁布的修订版。
ASTM C1784方法是一种基于传统稳态热流计法隔热性能测试技术(HFM)的动态测试方法,称之为动态热流计法(DHFM),是为了解决板状大尺寸相变材料热性能测试的一种实验室级别测试方法,样品尺寸一般为边长100~300
mm之间的正方形板材,这种尺寸易于从定形相变复合材料实际板材中取样测试,与DSC测试中毫克量级样品形式相比更具有材料的代表性。
本文针对测试定形相变材料热性能的ASTM C1784动态热流计法(DHFM),采用基于Modelica语言的SimulationX软件,建立测试热焓和比热容的模拟仿真模型,对测试方法开展更深入的研究。通过对不锈钢和沙子样品材料的测试模拟仿真,优化了试验参数,使得动态热流计法更容易被理解、掌握和推广应用。
2. 动态热流计法基本原理
动态热流计法(DHFM)是基于传统稳态热流计法(HFM)测量仪器上的一种动态测试方法,在稳态时可测量样品的导热系数,在动态时可测量样品的热焓和比热容。如图2-1所示,动态热流计法测试仪器结构与稳态热流计法测试仪器基本相同,不同之处是在样品的上下两面都安装有热流传感器,而且上下加热板的温度变化使用相同且同步。
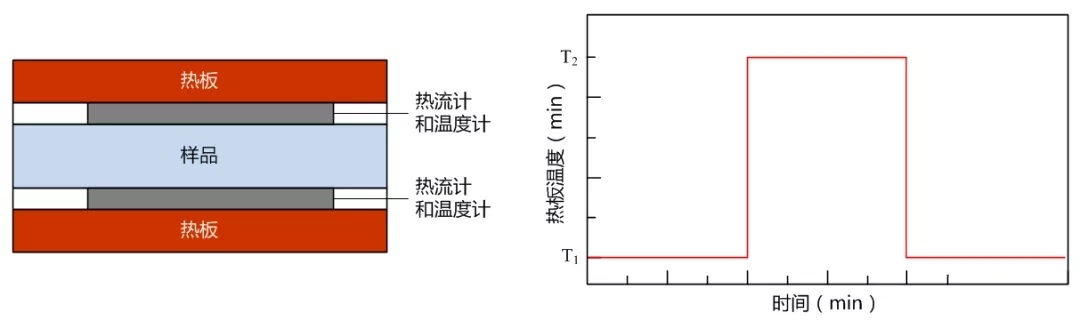
图2-1 动态热流计法测量原理
按照ASTM C1784规定,两个热板为台阶式升降温方式,如图2-1所示,当样品和上下热板在初始温度T1时达到稳态,将上下两个热板台阶式升温到另一个温度T2并达到恒定。这个温度变化过程中的测量不再时稳态测量而是非稳态测量,但记录了样品两侧的温度和热流密度随时间的变化,经过一定时间后两个均热板再次冷却到初始温度T1,这是一个典型的台阶式升降温测试过程。在此温度变化ΔT范围内,样品吸收的总热焓Δh可以通过对热流密度进行时间积分计算得到,而热容Cp则等于Δh/ΔT。
3. 测试仿真模型和参数
为了建立仿真模型进行瞬态分析计算,使用了SimulationX软件。SimulationX是基于Modelica语言模型的一维仿真软件之一,而Modelica是基于模型设计的基础设计研究的语言模型之一,采用模块式结构可以非常快速的设计仿真模型,仿真模型的物理意义直观和明确,能完美结合传统的热阻网络分析方法,非常适合瞬态传热的快速仿真计算,较传统的有限元瞬态分析方法的速度大为提高,可以在几秒内完成整个瞬态传热过程的模拟分析计算。
在采用SimulationX建模中,样品尺寸设置为300 mm×300 mm×20 mm,初始温度为20℃,对样品的两个表面按照相同的温度波形程序同时进行加热到30℃。
建模分析中采用了两种典型材料,其中不锈钢304的热物性参数分别是:导热系数为14.9 W/mK,比热容为0.477
J/gK,密度为7900 kg/m3。沙子的热物性参数分别是:导热系数为0.60 W/mK,比热容为0.80
J/gK,密度为1515 kg/m3。
4. 无热损情况下的模仿仿真
首先在无热损的理想条件下对准稳态法进行仿真模拟。在无侧向热损条件下,分别有两个热流计检测进出样品的热流量大小,同时假设样品是中心截面对称,并不考虑样品侧面的边缘热损。由此采用SimulationX软件设计的仿真模型如图4-1所示,分别模拟仿真不锈钢和沙子两种典型不同导热系数材料的比热容动态热流计法测试过程,计算得到比热容结果。最终将模拟仿真计算结果与设定的参数值进行比较,由此考核动态热流计法在理想情况下的测量准确性和合理的试验方法。
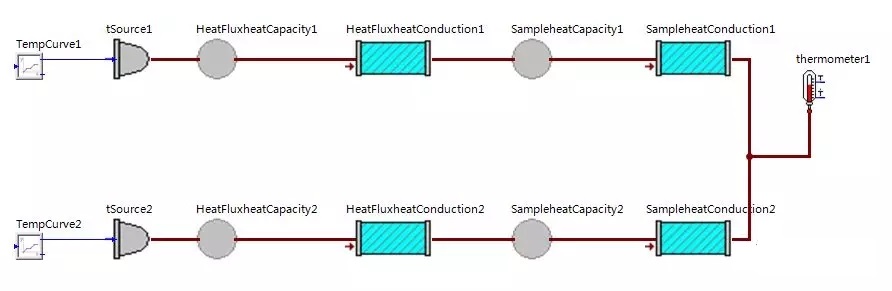
图4-1 使用SimulationX软件建立的无侧向热损仿真模型
4.1. 不锈钢比热容测量的模拟计算
首先对不锈钢304材料进行模拟仿真计算,按照ASTM标准方法规定,加热采用一个方波形式。在方波加热过程中,方波加热时温度变化,以及仿真模拟计算得到的不锈钢样品中心温度和进出样品的热流变化如图4-2所示。通过对上述热流随时间变化曲线按照时间进行积分,最终得到此波形加热过程中的单位质量不锈钢样品的热焓值变化曲线,如图4-3所示。
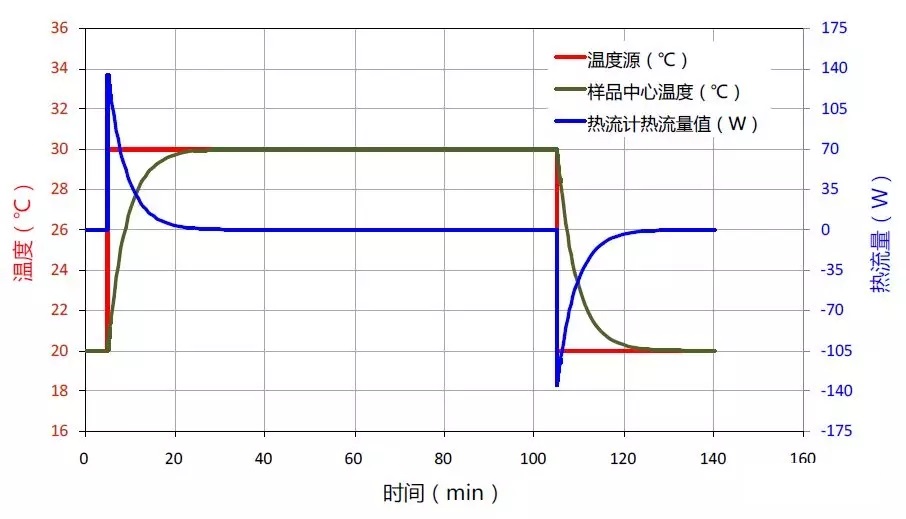
图4-2 矩形加热波形时不锈钢样品温度和热流变化曲线
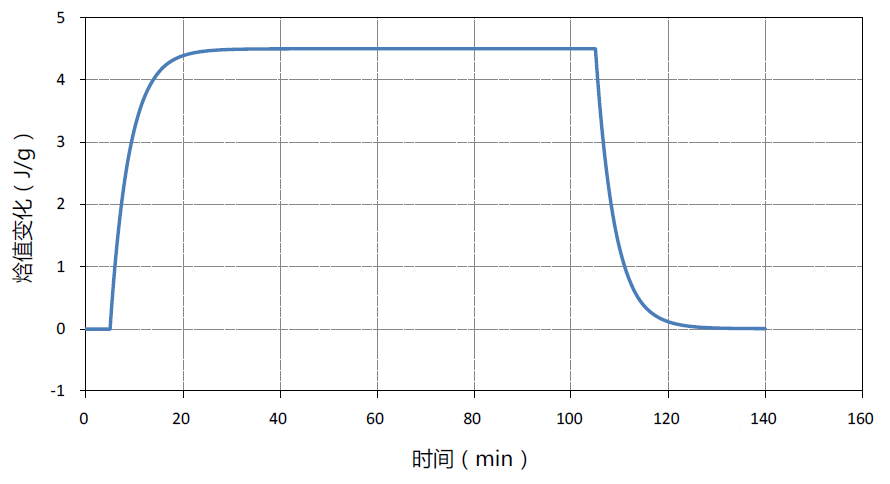
图4-3 矩形加热波形时单位质量不锈钢样品热焓值变化曲线
根据图4-3所示的模仿仿真结果,可以计算出20~30℃温度范围内不锈钢平均比热容为0.450 J/gK,与设定值0.477
J/gK的相对误差为5.7%。
通过图4-2所示的热流量随时间变化曲线可以看出,对热流量变化曲线进行积分相当于求此曲线相对于时间坐标轴所包含的面积,而对图4-2中如此突变的尖峰信号进行积分,由于时间间隔选取不可能无限小,这势必会带来积分误差,由此可见,对于方波加热形式,温度的突变是造成仿真计算误差的直接原因。在试验测试过程中,由于数据采集速度不可能很快,时间间隔也不可能非常小,这同样会带来相应测量误差。
4.2. 沙子比热容测量的模拟计算
同样,在方波加热过程中,计算得到的沙子样品中心温度和进出样品的热流变化如图4-4所示。通过对上述热流随时间变化曲线按时间进行积分,最终得到此波形加热过程中的单位质量沙子样品的热焓值变化曲线,如图4-5所示。
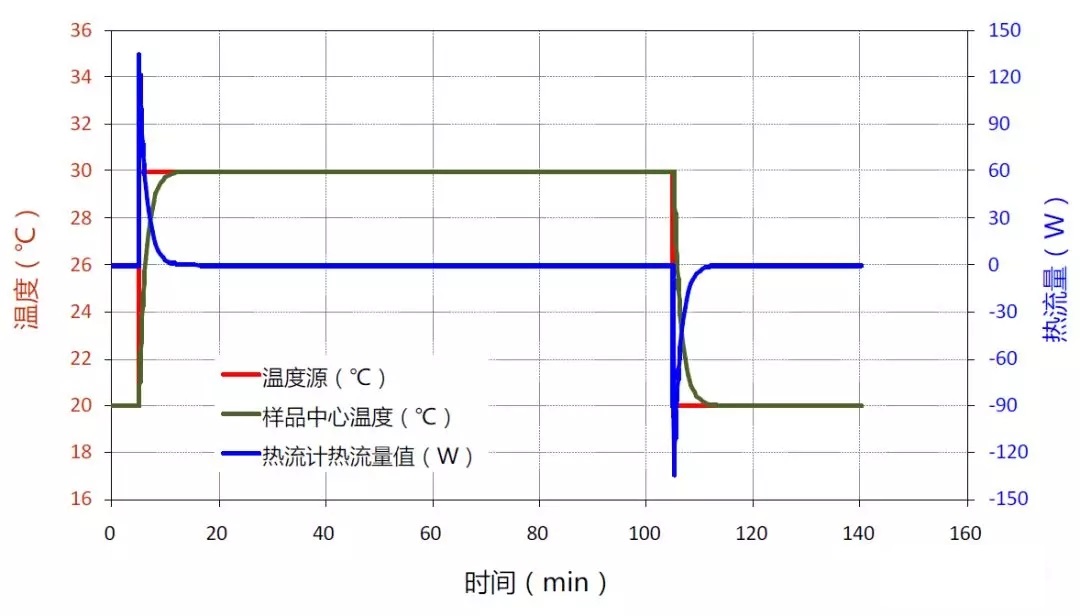
图4-4 矩形加热波形时沙子样品温度和热流变化曲线
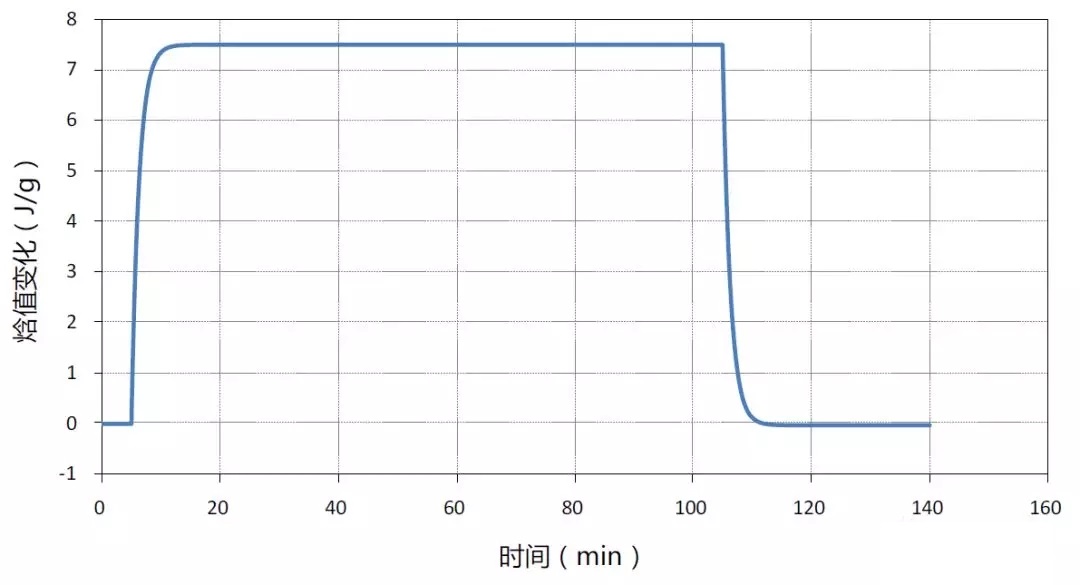
图4-5 矩形加热波形时单位质量沙子样品热焓值变化曲线
根据图4-5所示的模仿仿真结果,可以计算出20~30℃温度范围内沙子平均比热容为0.750 J/gK,与设定值0.80
J/gK的相对误差为6.3%。
4.3. 改变加热波形的模拟计算结果
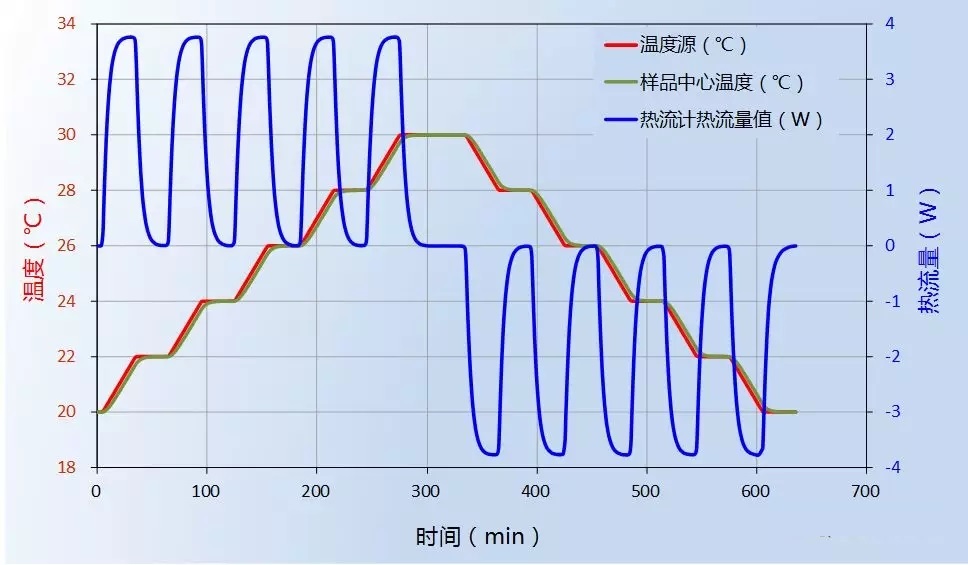
鉴于上述方波加热波形仿真计算结果有较大误差,对于304不锈钢材料样品,将加热波形调整为梯形,如图4-6中的红线所示,用时30分钟温度从20℃线性升温到30℃后恒温40分钟,然后按照相同的变温速率用时30分钟再降到20℃。
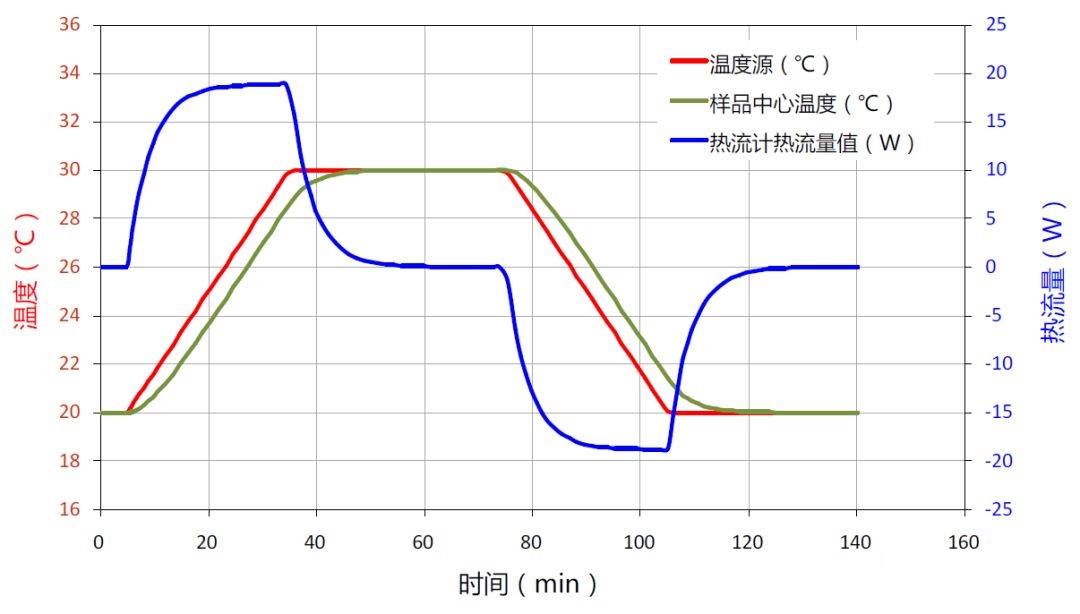
图4-6 改变加热波形后的不锈钢样品温度和热流变化曲线
在这种加热波形下,计算得到的样品中心温度和进出样品的热流变化如图4-6所示。通过对上述热流随时间变化曲线按照时间进行积分,最终得到此波形加热过程中的单位质量不锈钢样品的热焓值变化曲线,如图4-7所示。
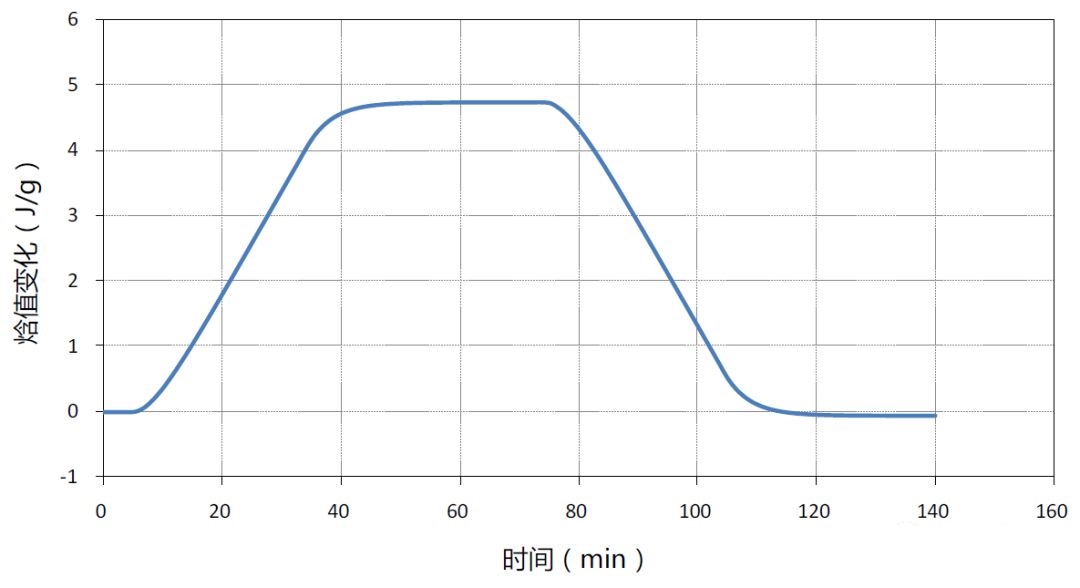
图4-7 梯形加热波形时单位质量不锈钢样品热焓值变化曲线
根据图4-7所示的模仿仿真结果,可以计算出20~30℃温度范围内的304不锈钢平均比热容为0.473
J/gK,与设定值相比没有误差,这说明通过改变加热波形,降低加热温度突变速率,可显著提高积分计算精度,大幅度减少最终计算结果误差。
同样,对于沙子材料样品,将加热波形调整为梯形,如图4-8中的红线所示,用时30分钟温度从20℃线性升温到30℃后恒温40分钟,然后按照相同的变温速率用时30分钟再降到20℃。
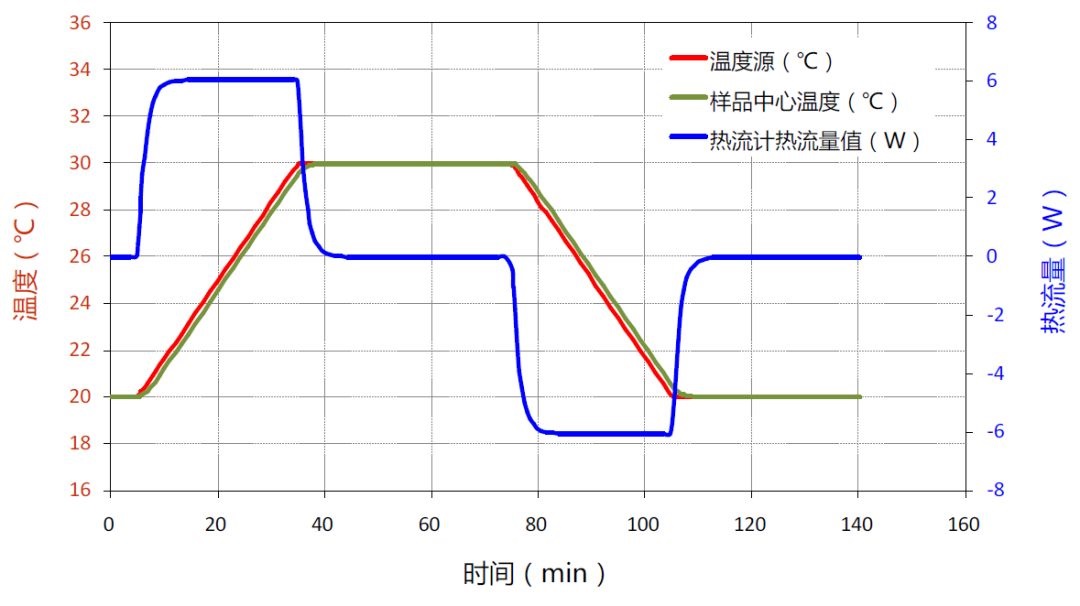
图4-8 改变加热波形后的沙子样品温度和热流变化曲线
在这种加热波形下,计算得到的样品中心温度和进出样品的热流变化如图4-8所示。通过对上述热流随时间变化曲线按照时间进行积分,最终得到此波形加热过程中的单位质量样品的热焓值变化曲线,如图4-9所示。
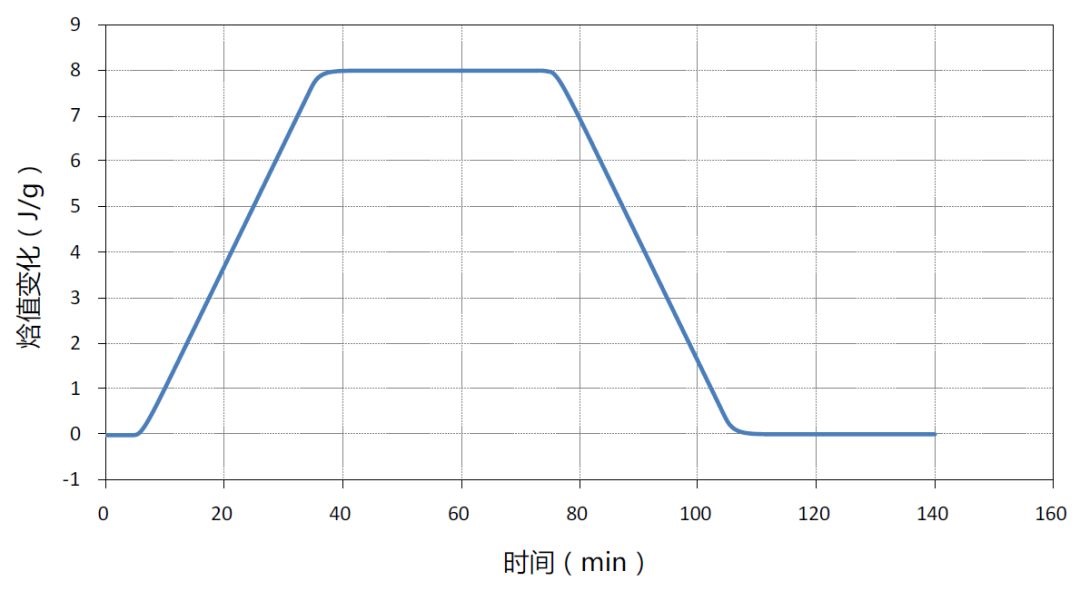
图4-9 梯形加热波形时单位质量沙子样品热焓值变化曲线
根据图4-9所示的模仿仿真结果,可以计算出20~30℃温度范围内的平均比热容为0.799 J/gK,与设定值相比没有误差,这说明通过改变加热波形,降低加热温度的突变速率,可显著提高积分计算精度,大幅度减少最终计算结果误差。
5. 有热损条件下的模仿仿真
上述仿真模拟是假设样品侧向无热损,而在实际测试条件下,样品侧面尽管采用了低导热材料进行防护,但还是存在侧向热损。为此,针对热流计法导热仪结构建立带热损效应的仿真模型,如图5-1所示。
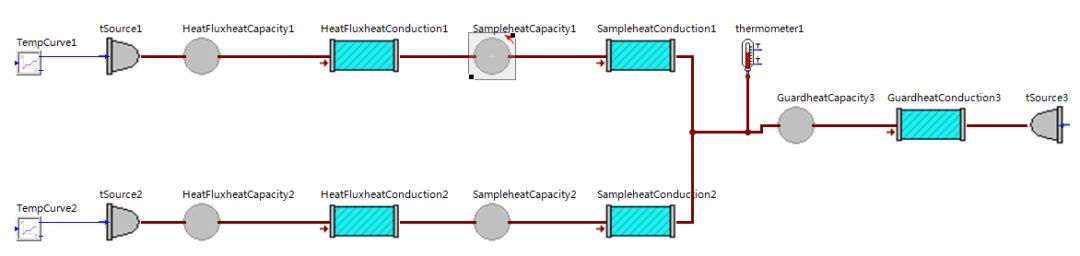
图5-1 使用SimulationX软件建立的存在侧向热损仿真模型
其中假设样品侧向热防护材料为软木,软木导热系数为0.048 W/mK,比热容为2.03 J/gK,密度为86
kg/m3,软木截面积为300 mm×20 mm,厚度为50 mm,软木的外侧温度始终保持为20℃。考虑到样品的四个侧面都有软木隔热材料,所以侧面仿真模型中的软木尺寸应为截面积为300
mm×80 mm,厚度为50 mm。
为了便于观察热损的影响,对沙子样品进行了有热损情况下的模拟仿真计算,结果如图5-2所示。从图5-2中可以看出,当有侧向热损存在时,样品达到热平衡后,焓值随时间的变化并未呈水平方向的曲线形式,而是向上倾斜,而且焓值要比无热损时要大(误差将近10%左右),这证明其中有一部热量被侧向热损带走,因此在实际测试中要对测试曲线进行侧向热损修正。
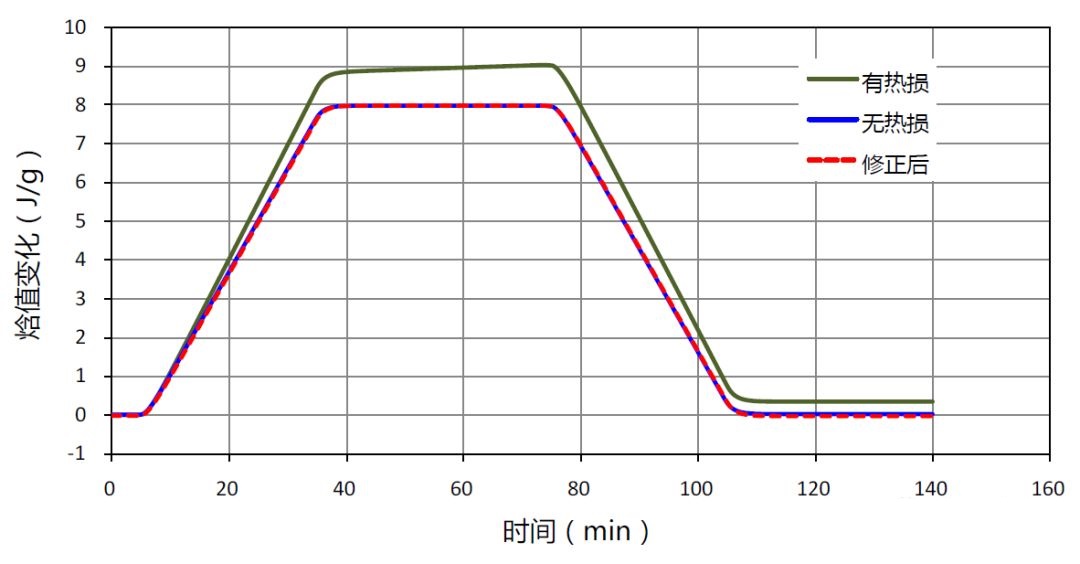
图5-2 沙子样品有热损、无热损和修正后的模拟仿真计算结果
从图5-2中的修正后结果可以看出,修正后的结果与无热损计算结果完成重合,修正后的比热容为0.80
J/gK,与设定值0.8 J/gK的相对误差基本为零。
同样,对不锈钢样品进行有热损存在时的模拟仿真计算结果证明也存在相同规律,如图5-3所示,修正后的误差基本为零。
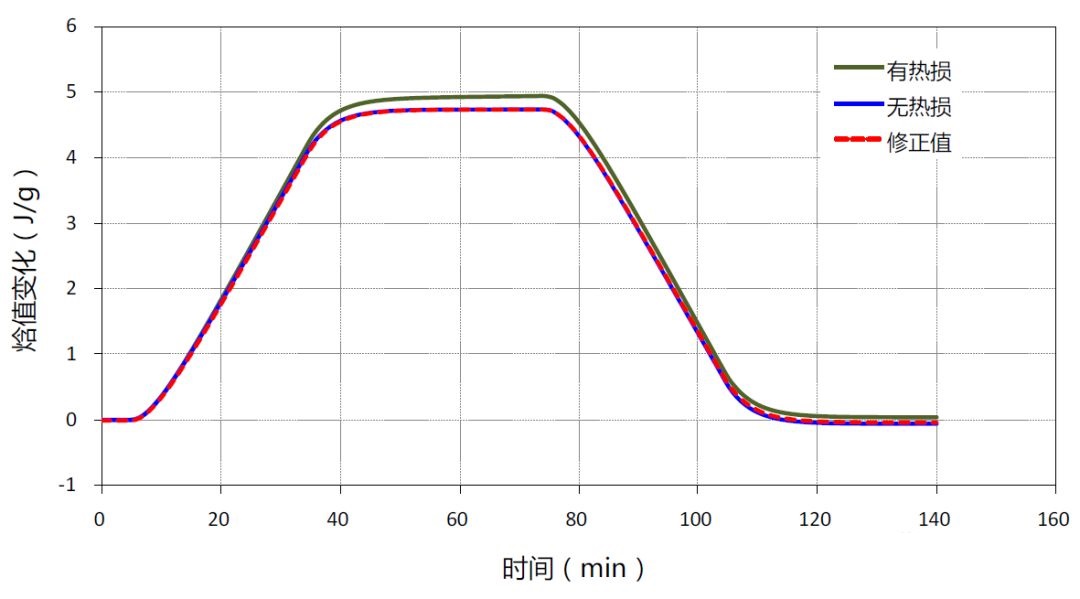
图5-3 不锈钢样品有热损、无热损和修正后的模拟仿真计算结果
6. 结论
综上所述,采用SimulationX软件的动态仿真模拟,计算了不锈钢和沙子材料的热焓和比热容动态热流法测量结果,由此可得出以下结论:
(1)采用动态热流计法以及相应的修正手段,可以准确测量样品的热焓和热容随温度的变化,证明了ASTM
C1784的有效性。
(2)在动态热流计法实际应用中,并不能完全采用ASTM C1784中规定的方波加热方式,因为这种突变型的变温方式会对测量数据处理带来较大误差,更准确的变温方式应为变化较缓慢的梯形的升降温方式。
(3)动态热流计法本质上还是属于一种稳态法,只是将大的温度区间分割为许多个小温度区间进行测试,按照ASTM中的规定,单个测试温度区间一般设定为1.5℃±0.5℃,由此来覆盖相变材料的相变温度变化范围,由此带来的问题就是测试时间十分漫长,通过上述仿真分析也得到了证明这个特点。 |

