Introduction: what is it supposed to do ?

I dedicated myself to creating a .NET component that allows the building of graphs and the performance of some operations on these structures. In particular A*, the famous path finding algorithm, can be run to find the best path between two places.

First and foremost it should be kept in mind that a graph is defined with :

• A list of nodes
• A list of arcs

Each node is defined with the following data :

• A geographical position in space (co-ordinates X,Y,Z)
• The collection of the outgoing arcs
• The collection of the incoming arcs

Each arc is simply defined with its two extremity nodes. So an arc is oriented from StartNode to EndNode. It is also characterized by a crossing factor named 'Weight'. This value represents the difficulty to reach the ending node from the starting one. Thus, getting through an arc has a cost, which can be basically calculated like this :

Cost = Distance(StartNode, EndNode) * Weight

You may be asking "What is the use of this structure ?...". Well, the applications can be various, ranging from road maps and circulation models to a character's mobility in a video game. Now the question is: "How one would move across this graph ?".

What is A* ?

Imagine that you are on a node and that you want to reach another position somewhere else on the graph. Then ask : "Which way will I follow, and why ?". The main factor to take into account here is the cost of moving. It must be minimal. The cost criterion is basically a function of the distance (sum of arcs' lengths). However, it can also be adjusted and varied with other data, which describe for example the slope, the harshness/practicability of the ground. You can even model a traffic jam.

To achieve the best path, there are many algorithms which are more or less effective, depending on the particular case. Efficiency depends not only on the time needed for calculation, but also on the reliability of the result. A* is able to return the best path (if it exists) between two nodes, according to accessibility/orientation and, of course, cost of arcs.

Among the variety of existing algorithms, some do not always actually return the best path, but they can give precedence to speed over accuracy. Efficiency depends on the number of nodes and on their geographical distribution. However in most cases A* turns out to be the most effective, because it combines optimized search with the use of a heuristic.

A heuristic is a function that associates a value with a node to gauge it. One node is considered better than another, if the final point is reached with less effort (e.g. shorter distance).

A* will always return the shortest path if, and only if, the heuristic is admissible; that is to say, if it never overestimates. On the other hand, if the heuristic is not admissible, A* will find a path in less time and with less memory usage, but without the absolute guaranty that it is the best one. Here are three admissible heuristics which correspond to a particular distance between the node of evaluation and the target node :

• Euclidean distance > Sqrt(Dx²+Dy²+Dz²)
• Manhattan distance > |Dx|+|Dy|+|Dz|
• Maximum distance > Max(|Dx|, |Dy|, |Dz|)

These functions give an estimation of the remaining distance for each node that can be explored. Thus the search can be oriented toward the 'best' nodes. For a given node, the sum [Current cost + Heuristic value] is an estimation of the cost of reaching the ending node from the starting node, passing by the current one. This value is used to continuously choose the most promising path.

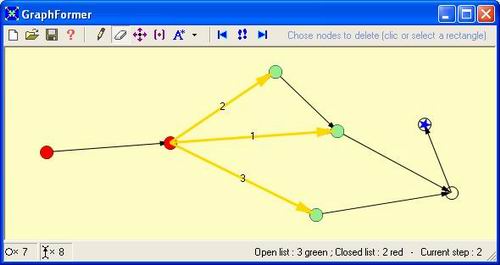
In practice, the algorithm maintains 2 lists of nodes that are filled and modified during the search :

1. The first one, called Open, contains the tracks leading to nodes that can be explored. Initially, there is only the starting node. At each step, the best node of Open is taken out. Then, the best successor of this node (according to the heuristic) is added to the list as a new track. One doesn't know where the nodes that are in Open lead, because they have not been propagated yet. However, the best one is examined at each new step.
2. The second one, called Closed, stores the tracks leading to nodes that have already been explored.

The program is based on a recursive model. The loop is performed as long as Open still contains some elements. See the code for details (written with C#, it is sufficient enough to be self explainable).

public bool SearchPath(Node StartNode, Node EndNode)
{
    lock (_Graph)
    {
        Initialize(StartNode, EndNode);
        while ( NextStep() ) {}
        return PathFound;
    }
}

Using the code: public interfaces of the component

The Graph class gathers a set of methods to manage its data, such as :

• Add/Suppress a node/arc
• Get the nearest/farthest node/arc from a point
• Activate/Inactivate the entire graph
• Empty the graph

From a more practical point of view, here are the methods and properties you can use for the main classes and objects :

public class Graph
{
    public Graph()

    public IList Nodes { get }
    public IList Arcs { get }

    public void Clear()
    public bool AddNode(Node NewNode)
    public Node AddNode(float x, float y, float z)
    public bool AddArc(Arc NewArc)
    public Arc AddArc(Node StartNode, Node EndNode, float Weight)
    public void Add2Arcs(Node Node1, Node Node2, float Weight)
    public bool RemoveNode(Node NodeToRemove)
    public bool RemoveArc(Arc ArcToRemove)
    public void BoundingBox(out double[] MinPt, out double[] MaxPt)
    public Node ClosestNode(double X, double Y, double Z, out double Dist, 
                            bool IgnoreFreeWay)
    public Arc ClosestArc(double X, double Y, double Z, out double Dist, 
                            bool IgnoreFreeWay)
}

public class Node
{
    public Node(double PositionX, double PositionY, double PositionZ)

    public IList IncomingArcs { get }
    public IList OutgoingArcs { get }
    public double X { get }
    public double Y { get }
    public double Z { get }
    public void ChangeXYZ(double PositionX, double PositionY, 
                          double PositionZ)
    public bool Passable { get/set }

    public Node[] AccessibleNodes { get }
    public Node[] AccessingNodes { get }
    public void UntieIncomingArcs()
    public void UntieOutgoingArcs()
    public void Isolate()
    public Arc ArcGoingTo(Node N)
    public Arc ArcComingFrom(Node N)
    public object Clone()

    public static void BoundingBox(IList NodesGroup, out double[] MinPt, 
                                   out double[] MaxPt)
    public static double EuclidianDistance(Node N1, Node N2)
    public static double SquareEuclidianDistance(Node N1, Node N2)
    public static double ManhattanDistance(Node N1, Node N2)
    public static double MaxDistanceAlongAxis(Node N1, Node N2)

    public override string ToString()
    public override bool Equals(object O)
    public override int GetHashCode()
}

public class Arc
{
    public Arc(Node Start, Node End)

    public Node StartNode { get/set }
    public Node EndNode { get/set }
    public double Weight { get/set }
    public bool Passable { get/set }

    virtual public double Cost { get }
    public double Length { get }
    virtual protected double CalculateLength()

    public override string ToString()
    public override bool Equals(object O)
    public override int GetHashCode()
}

public class AStar
{
    public AStar(Graph G)

    public bool SearchPath(Node StartNode, Node EndNode)
    public void Initialize(Node StartNode, Node EndNode)
    public bool NextStep()

    public bool Initialized { get }
    public int StepCounter { get }
    public bool SearchStarted { get }
    public bool SearchEnded { get }
    public bool PathFound { get }
    public Node[] PathByNodes { get }
    public Arc[] PathByArcs { get }
    public bool ResultInformation(out int NbArcsOfPath, out double CostOfPath)

    public double DijkstraHeuristicBalance { get/set }
    public Heuristic ChoosenHeuristic { get/set }
    public static Heuristic EuclidianHeuristic { get }
    public static Heuristic MaxAlongAxisHeuristic { get }
    public static Heuristic ManhattanHeuristic { get }
}

Nodes and arcs can be Passable or not. Selecting one of these two states for a node, propagates the same state to outgoing and incoming arcs. Likewise, destroying a node implies the destruction of all the directly linked arcs. In addition, an arc must always be linked to two nodes, whereas a node can be isolated.

Note that these data override Object.ToString() as well as Object.Equals(Object O). Moreover they can be serialized.

Simple example of the usage with the console application

using System;
using System.Collections;
using System.Text;
using System.IO;
using System.Runtime.Serialization;
using System.Runtime.Serialization.Formatters.Binary;
using EMK.Cartography;

namespace EMK.Tests
{
    public class TestAStar
    {
        public static void Main()
        {
            try
            {
                Graph G = new Graph();
                Node N1 = G.AddNode(0,0,0);
                Node N2 = G.AddNode(5,0,0);
                Node N3 = G.AddNode(5,5,0);
                Node N4 = G.AddNode(5,5,5);
                G.AddArc(N1,N2,1);
                G.AddArc(N2,N3,1);
                G.AddArc(N3,N4,1);
                G.AddArc(N1,N3,1);

                Console.WriteLine( ListNodesAndArcs(G) );
                Console.WriteLine("Best path to reach "+N4+" from "+N1+" :");
                AStar AS = new AStar(G);
                if ( AS.SearchPath(N1, N4) )
                    foreach (Arc A in AS.PathByArcs) 
                        Console.WriteLine( A.ToString() );
                else Console.WriteLine( "No result !" );

                Console.Write("Serialize and Deserialize. ");
                Stream StreamWrite = File.Create("GraphSaved.bin");
                BinaryFormatter BinaryWrite = new BinaryFormatter();
                BinaryWrite.Serialize(StreamWrite, G);
                StreamWrite.Close();

                Stream StreamRead = File.OpenRead("GraphSaved.bin");
                BinaryFormatter BinaryRead = new BinaryFormatter();
                Graph G2 = (Graph) BinaryRead.Deserialize(StreamRead);
                StreamRead.Close();
                Console.WriteLine( ListNodesAndArcs(G2) );
            }
            catch(Exception e) 
            { 
                Console.Write( "Error :\n\n"+e.ToString() ); 
            }
        }

        static private string ListNodesAndArcs(Graph GraphToDescribe)
        {
            StringBuilder SB = new 
                StringBuilder("Description of the Graph:\n\tNodes> ");
            foreach (Node N in GraphToDescribe.Nodes) 
                SB.Append( N.ToString()+"; " );
            SB.Append("\n\tArcs> ");
            foreach (Arc A in GraphToDescribe.Arcs) 
                SB.Append( A.ToString()+"; " );
            return SB.ToString();
        }
    }
}

Description of the Graph:
        Nodes> {0;0;0}; {5;0;0}; {5;5;0}; {5;5;5}
        Arcs> {0;0;0}-->{5;0;0}; {5;0;0}-->{5;5;0}; 
                    {5;5;0}-->{5;5;5}; {0;0;0}-->{5;5;0}
Best path to reach {5;5;5} from {0;0;0} :
{0;0;0}-->{5;5;0}
{5;5;0}-->{5;5;5}
Serialize and Deserialize. Description of the Graph:
        Nodes> {0;0;0}; {5;0;0}; {5;5;0}; {5;5;5}
        Arcs> {0;0;0}-->{5;0;0}; {5;0;0}-->{5;5;0}; 
                    {5;5;0}-->{5;5;5}; {0;0;0}-->{5;5;0}

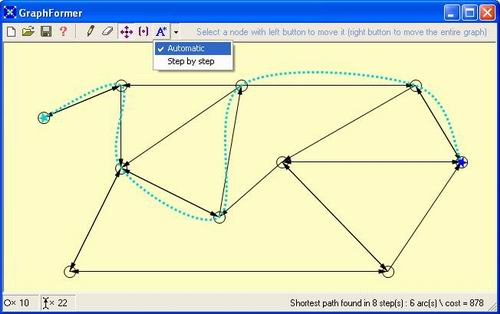
Example of use in a graphical environment

The graphical interface aims at bringing the component into play so as to reflect, fairly and simply, what it can do. The application lets you draw, move, erase or inactivate several nodes and arcs. When your graph is complete you just have to click on the 'A*' icon and select the starting and ending nodes with the respective left and right mouse buttons. Then you will automatically see the best way. If you modify the graph, this path will be updated.

If you want to visualize the algorithm's logic, then select the 'Step by Step' mode in the sub-menu of the 'A*' icon. The idea is to give the user a clear view of what happens.

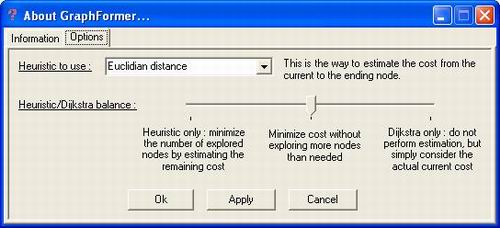
In the option panel ('?' icon), you can change the heuristic and set its influence. The min value (in fact 0) means that only the heuristic will be used. On the contrary, the max value (in fact 1) means that the search will behave in accordance with the Dijkstra algorithm.

Remarks

The program has been validated with a series of adapted tests, gathering various scenarios and interactions. Nevertheless it does not aim to be a perfect application, but an unassuming program that modestly claims to be simple and ergonomic. For information, I had already done this work with C++ for the DLL as well as MFC for the 2D graphical interface. I had also tested it in a 3D context with an OpenGL graphical interface. The next step will be to implement the 3D interface with Direct3D 9.0 for .NET or with one of the OpenGL solutions for this framework.

The source code contains a light but interesting implementation of geometrical tools such as Point3D and Vector3D. They were needed for graphical interactions in the GraphFormer example application (projections on lines, vectors' operations, etc...).

For convenience and performance I used the SortableList type for Closed and Open lists. The advantage is that, the best track will always be the first element, since the list remains sorted (cf the article I have written formerly about Automatic Sorted List). Nonetheless it would be very easy to replace it with another list type, such as ArrayList, provided you look for the 'best' element (that is to say the lower) at each step.