应用背景
1.1 解决的问题
1)大型企业的 IT 系统对每一次应用程序的升级都会预先在其测试环境上进行测试。如何保证测试的有效性?如何通过测试的结果推测其在生产环境上的表现?
2)随着资源使用的增长,CPU、内存、硬盘、I/O 等资源互相影响并存在潜在关联。如何洞察其关联来指导企业做出合理的容量规划?
3)伴随业务扩展,企业生产环境的负载日益增加。 如何帮助企业通过对未来业务量和用户量的增长预测而做出相应的容量预估?
4)如何提供自动化、自适应的建模过程与预测分析,为企业用户打造针对个性化场景自动建立、自动调整的预测模型来降低使用复杂度?
如何保证预测分析的有效性和准确性?
1.2 商业价值
1)避免过多地投入测试资源,最大化测试资源价值,实现测试与生产的资源整合。
2)优化企业数据中心资源利用率,各项资源合理配比,提供更精准的性能分析和容量规划方案以节约成本。
3)合理预测业务增长,提高企业对未来业务的洞察力,帮助企业制定更完备的容量预估和应急方案。
4)提升业务可持续性与用户体验,为企业提供基于源数据的自动化选型、建模、调整、验证的全生命周期解决方案。
2. 数据准备
应用某网站在新业务上线前,通过测试环境的结果预测其生产环境上线后的资源利用率场景。从小范围入手,首先针对一台服务器,选取相关指标数据进行关联分析与预测建模的研究。例如在众多的服务器中,选取其中的一台
web 服务器(192.168.119.9)。对该台服务器在 2013 年 1 月 1 日 00:00~24:00
的各项指标,采集单位为分钟,共 1440 条数据进行量化分析。
本文的主要目的是预测用户访问频率 Frequency_User 的未来发展趋势。因此,需要考虑用户访问频率
Frequency_User、内存利用率 MEM、硬盘利用率 DISK 与 CPU 利用率的关系。将数据文件的信息合并为一个新的数据文件,数据整理后的文件被保存成
IBM SPSS Statistics 的 SAV 格式的存储文件,如图 1 所示,其中包含以下字段:日期
DATE、时间 TIME(采集单位:分钟)、用户访问频率 Frequency_User(单位 : 次)、内存利用率
MEM(单位:%)、硬盘利用率 DISK(单位:%)、用户 CPU 利用率 CPU(单位:%)。
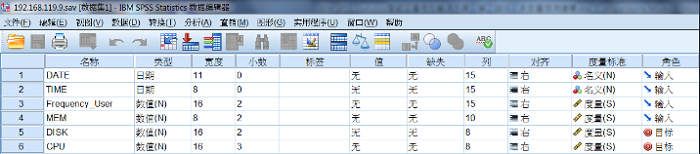
图 1. 数据文件变量
3. IBM SPSS Statistics 使用过程
3.1 多变量关联分析
本文通过偏相关分析,判断用户访问频率 Frequency_User 与
CPU 利用率、内存利用率 MEM、硬盘利用率 DISK 之间的关联关系。偏相关分析是当两个变量同时与其他多个变量相关时,将其他多个变量的影响剔除,只分析另外两个变量之间相关程度的过程
。因此,针对于本文中包含的多个变量的关联分析,可利用偏相关分析展开研究。例如分析其中的两个变量访问频率
Frequency_User 与 CPU 利用率的关联关系,需要剔除内存利用率 MEM 与硬盘利用率 DISK
的影响,只针对于访问频率 Frequency_User 与 CPU 利用率进行偏相关分析。通过相关系数
r,判断 Frequency_User 与 CPU 是否线性相关。若线性相关,则可得出关联关系。若不线性相关,则利用回归判断出目标变量与其他多个变量间的影响关系,即判断预测变量的重要性对于目标变量。多变量关联分析流程图,如下图
2 所示 。
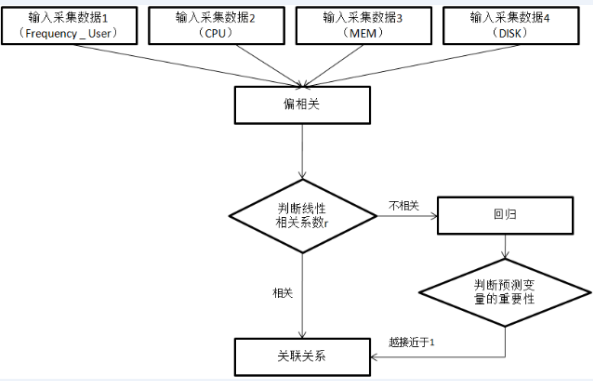
图 2. 多变量关联分析流程图
3.1.1 偏相关分析
1) 偏相关分析步骤
打开 IBM SPSS Statistics,在菜单中选择:分析 >
相关 > 偏相关, 就进入“偏相关” 模块方法界面,如图 3 所示。
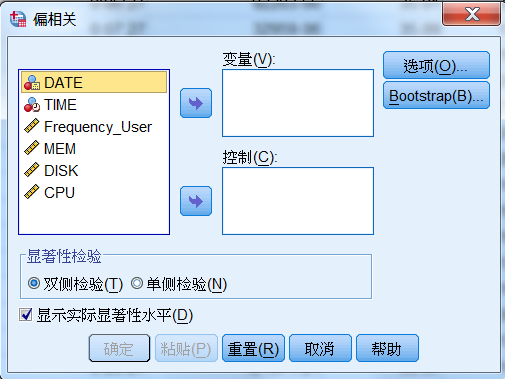
图 3. 偏相关分析界面
在“偏相关”对话框中,选择 Frequency_User 与 CPU 进入“变量”框,选择
MEM 与 DISK 进入“控制”框。在“显著性检验”框中可选相关系数的单侧(One-tailed)或双侧(Two-tailed)检验,
本文选双侧检验,如图 4 所示。
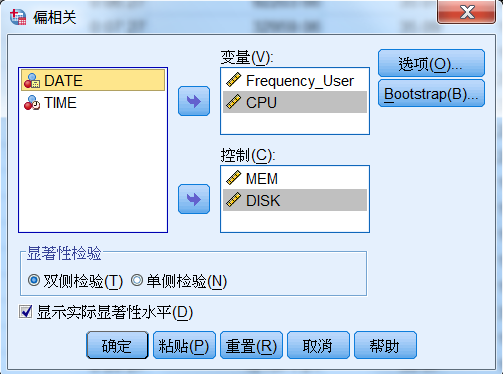
图 4. 选择变量与参数
点击“选项”按钮弹出“偏相关性:选项”对话框,可设置相关统计量,如图 5
所示。本文设置 Frequency_User、CPU、MEM 与 DISK 输出“均数与标准差”以及“零阶相关系数”,点击“继续”按钮返回“偏相关”对话框。
图 5. 偏相关性选项
2)结果描述
根据偏相关分析的结果,Frequency_User 的均值为 85778.15992,标准差为
43387.93355;CPU 的均值为 33.84895%,标准差为 9.304364;MEM 的均值为
36.93768%,标准差为 6.954192;DISK 的均值为 30.71943%,标准差为 13.372261,如图
6 所示。
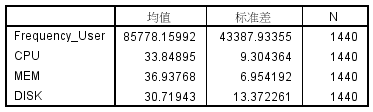
图 6. 描述性统计量
以下展示了两种偏相关关系的结果,如图 7 所示。首先,在没有控制变量的情况下,展示了
Frequency_User、CPU、MEM 与 DISK 两两对应的相关系数、双侧检验的概率与自由度。其次,在设定
MEM 与 DISK 为控制变量情况下,展示了 Frequency_User 与 CPU 两两对应的相关系数、双侧检验的概率与自由度。根据两种偏相关情况下的结果可以看出,若不剔除
MEM 与 DISK 对 Frequency_User、CPU 的影响,Frequency_User 与
CPU 的相关性系数为 0.622;若剔除 MEM 与 DISK 对 Frequency_User、CPU
的影响,Frequency_User 与 CPU 的相关性系数为 0.771。
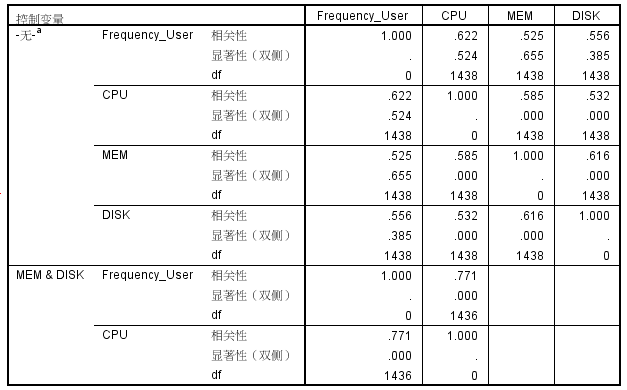
图 7. 相关性
其中,相关性的值为通常所指的相关系数 r。相关系数 r 较好地度量了两变量间的线性相关程度,相关系数
r 属于 [1,+1]。若 00.8:强相关;|r|<0.3:弱相关,可视为不相关。本文中 Frequency_User
与 CPU 的相关性的值为 0.771,还需利用回归分析进一步研究。
3.1.2 回归分析
1)回归分析步骤
打开 IBM SPSS Statistics,在菜单中选择:分析 >
回归 > 自动线性建模,就进入“自动线性 建模”模块方法界面,如图 8 所示。
图 8. 自动线性建模界面
在“自动线性建模”对话框中,选择 Frequency_User 为目标,CPU、DISK
与 MEM 为预测变量(输入),进行自动线性建模,如图 9 所示。
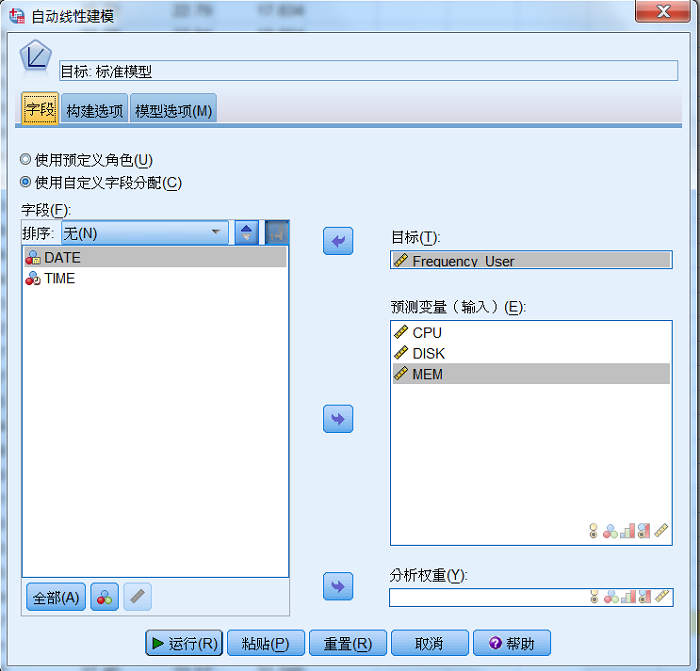
图 9. 自动线性建模界面
2)结果描述
根据预测变量的重要性,关联分析出 CPU 对 Frequency_User
的重要性达到 80% 以上,DISK 与 MEM 的重要性均没有超过 20%,如图 10 所示。充分表明
CPU 与 Frequency_User 的相关性最强,对其的解释能力最高。
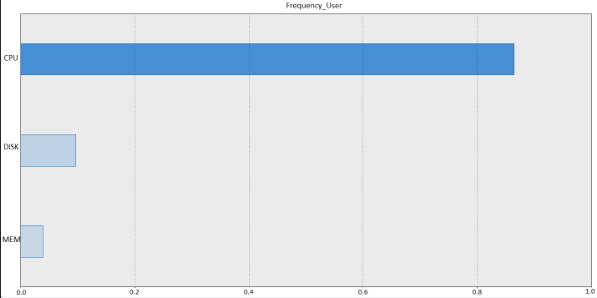
图 10. 预测变量重要性
3.2 预测建模
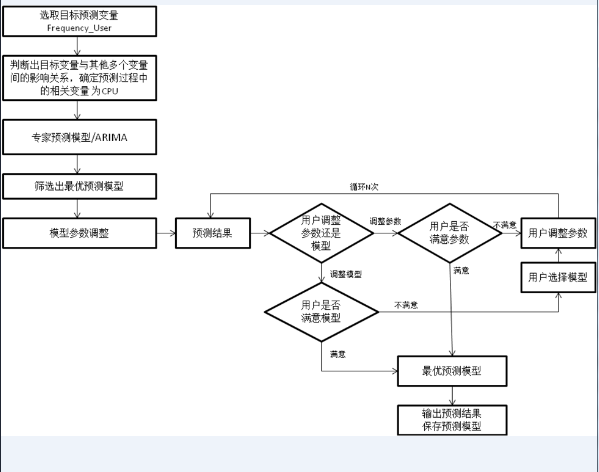
图 11. 预测模型的建模流程图
筛选出最优预测模型
1) 建模步骤
打开 IBM SPSS Statistics,在菜单中选择:分析 >
预测 > 创建模型,就进入 “时间序列建模器”模块方法界面,如图 12 所示。在“时间序列建模器”对话框中,选择
Frequency_User 为因变量,CPU 为自变量,建立多种预测模型。
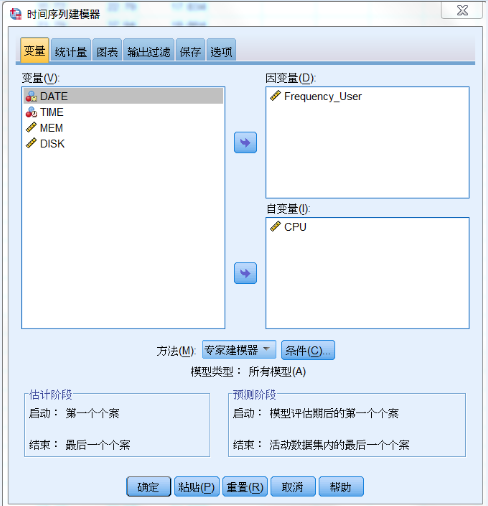
图 12. 时间序列建模器
在“统计量”标签中选择输出的拟合度量指标,例如:R 方,均方根误差,平均绝对误差百分比。在“图表”标签中选择每张图显示的内容为:观察值,预测值和拟合值。在“保存”标签中,一方面,设置保存预测模型的预测结果在
SAV 文件中;另一方面,将预测模型保存为 xml 格式,当有新的数据需要预测时,可直接使用此保存结果,不用重新构造模型,如图
13 所示。在“选项”标签中指定未来希望预测到的时间点,例如本文有 1 至 1440 分钟的观测值,指定预测值为
1500 分钟即可获得 1441 至 1500 分钟的预测值。
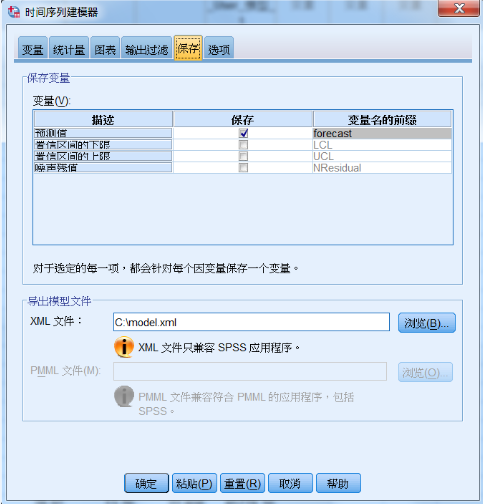
图 13. 保存预测模型
2)结果描述
根据拟合结果,选取最优的 ARIMA(1,1,0)预测模型进行建模,如图
14 所示。

图 14. 模型描述
输出的拟合度量指标,例如:R 方,均方根误差(RMSE),平均绝对误差百分比(MAPE),如图
15 所示。本文选取指标 R 方,RMSE,MAPE 对预测结果进行评价:R 方越接近于 1,MAPE
越接近于 0 表明模型的拟合程度越好;均方根误差说明了样本的离散程度。

图 15. 模型统计量
Frequency_User 的观察值、预测值和拟合值,如图 16 所示。其中,横坐标代表时间(间隔:分钟),纵坐标代表用户访问频率
Frequency_User(单位:次)。
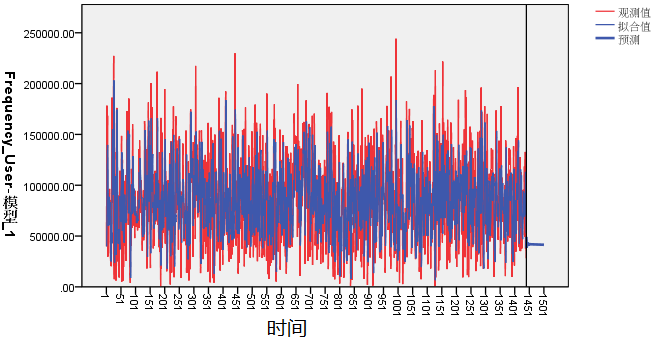
图 16. 预测模型的预测结果
模型参数调整
在“时间序列建模器”对话框,点击“条件”按钮,如图 17 所示。将进行预测模型的参数调整。
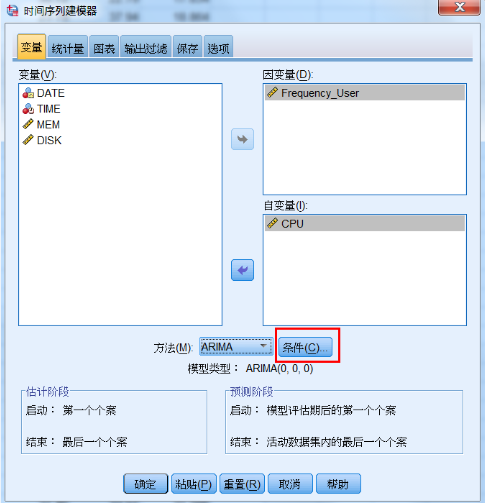
图 17. 模型参数调整
进入“时间序列建模器:ARIMA 条件”。ARIMA(p,d,q)称为差分自回归移动平均模型,AR
是自回归,p 为自回归项;MA 为移动平均,q 为移动平均项数,d 为时间序列成为平稳时所做的差分次数。
p、d、q 取值范围一般均为 [0,2],如图 18 所示。可设置不同的参数值进行预测建模。
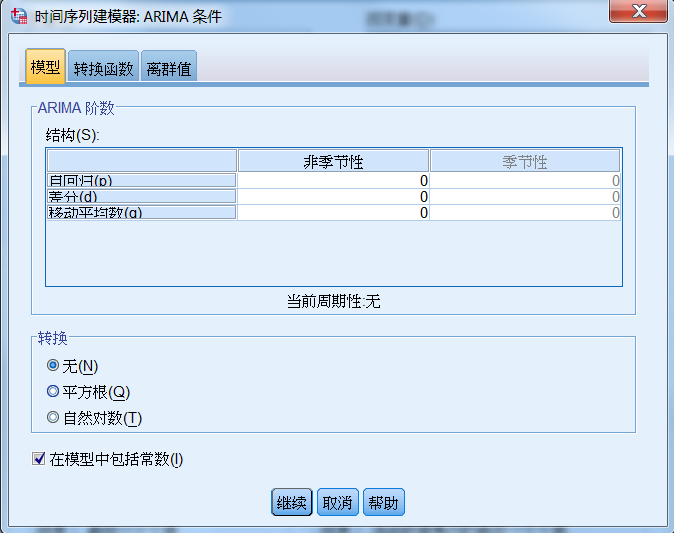
图 18.ARIMA 预测模型的分类
|

