随着计算能力、存储、网络的高速发展，人类积累的数据量正以指数速度增长。对于这些数据，人们迫切希望从中提取出隐藏其中的有用信息，更需要发现更深层次的规律，对决策，商务应用提供更有效的支持。为了满足这种需求，数据挖掘技术的得到了长足的发展，而分类在数据挖掘中是一项非常重要的任务，目前在商业上应用最多。本文主要侧重数据挖掘中分类算法的效果的对比，通过简单的实验（采用开源的数据挖掘工具 -Weka）来验证不同的分类算法的效果，帮助数据挖掘新手认识不同的分类算法的特点，并且掌握开源数据挖掘工具的使用。

简介

分类算法是解决分类问题的方法，是数据挖掘、机器学习和模式识别中一个重要的研究领域。分类算法通过对已知类别训练集的分析，从中发现分类规则，以此预测新数据的类别。分类算法的应用非常广泛，银行中风险评估、客户类别分类、文本检索和搜索引擎分类、安全领域中的入侵检测以及软件项目中的应用等等。

分类算法介绍

以下介绍典型的分类算法。

Bayes

贝叶斯分类器的分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类。目前研究较多的贝叶斯分类器主要有四种，分别是：Naive Bayes、 TAN、BAN 和 GBN。

1.贝叶斯网络（BayesNet）

贝叶斯网络是一个带有概率注释的有向无环图，图中的每一个结点均表示一个随机变量 , 图中两结点间若存在着一条弧，则表示这两结点相对应的随机变量是概率相依的，反之则说明这两个随机变量是条件独立的。网络中任意一个结点 X 均有一个相应的条件概率表 Conditional Probability Table，CPT) ，用以表示结点 X 在其父结点取各可能值时的条件概率。若结点 X 无父结点 , 则 X 的 CPT 为其先验概率分布。贝叶斯网络的结构及各结点的 CPT 定义了网络中各变量的概率分布。应用贝叶斯网络分类器进行分类主要分成两阶段。第一阶段是贝叶斯网络分类器的学习，即从样本数据中构造分类器，包括结构学习和 CPT 学习；第二阶段是贝叶斯网络分类器的推理，即计算类结点的条件概率，对分类数据进行分类。这两个阶段的时间复杂性均取决于特征值间的依赖程度，甚至可以是 NP 完全问题，因而在实际应用中，往往需要对贝叶斯网络分类器进行简化。根据对特征值间不同关联程度的假设，可以得出各种贝叶斯分类器。

2.朴素贝叶斯（NaiveBayes）

朴素贝叶斯模型（NBC）发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。同时，NBC 模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单。NBC 模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，这给 NBC 模型的正确分类带来了一定影响。在属性个数比较多或者属性之间相关性较大时，NBC 模型的分类效率比不上决策树模型。而在属性相关性较小时，NBC 模型的性能最为良好。

Lazy Learning

相对其它的 Inductive Learning 的算法来说，Lazy Learning 的方法在训练是仅仅是保存样本集的信息，直到测试样本到达时才进行分类决策。也就是说这个决策模型是在测试样本到来以后才生成的。相对与其它的分类算法来说，这类的分类算法可以根据每个测试样本的样本信息来学习模型，这样的学习模型可能更好的拟 合局部的样本特性。kNN 算法的思路非常简单直观：如果一个样本在特征空间中的 k 个最相似 ( 即特征空间中最邻近 ) 的样本中的大多数属于某一个类别，则该样本也属于这个类别。其基本原理是在测试样本到达的时候寻找到测试样本的 k 临近的样本，然后选择这些邻居样本的类别最集中的一种作为测试样本的类别。在 weka 中关于 kNN 的算法有两个，分别是 IB1，IBk。

1.IB1 即 1 近邻

IB1 是通过它的一个邻居来判断测试样本的类别

2.IBk 即 K 近邻

IBk 是通过它周围的 k 个邻居来判断测试样本的类别

在样本中有比较多的噪音点是（noisy points）时，通过一个邻居的效果很显然会差一些，因为出现误差的情况会比较多。这种情况下，IBk 就成了一个较优的选项了。这个时候有出现了一个问题，k 这个值如何确定，一般来说这个 k 是通过经验来判断的。

Trees

即决策树算法，决策树是对数据进行分类，以此达到预测的目的。该决策树方法先根据训练集数据形成决策树，如果该树不能对所有对象给出正确的分类，那么选择一些例外加入到训练集数据中，重复该过程一直到形成正确的决策集。决策树代表着决策集的树形结构。决策树由决策结点、分支和叶子组成。决策树中最上面 的结点为根结点，每个分支是一个新的决策结点，或者是树的叶子。每个决策结点代表一个问题或决策，通常 对应于待分类对象的属性。每一个叶子结点代表一种可能的分类结果。沿决策树从上到下遍历的过程中，在每个结点都会遇到一个测试，对每个结点上问题的不同的 测试输出导致不同的分支，最后会到达一个叶子结点，这个过程就是利用决策树进行分类的过程，利用若干个变量来判断所属的类别。

1.Id3 即决策树 ID3 算法

ID3 算法是由 Quinlan 首先提出的。该算法是以信息论为基础，以信息熵和信息增益度为衡量标准，从而实现对数据的归纳分类。

以下是一些信息论的基本概念：

定义 1：若存在 n 个相同概率的消息，则每个消息的概率 p 是 1/n，一个消息传递的信息量为 Log2(n)

定义 2：若有 n 个消息，其给定概率分布为 P=(p1,p2 … pn)，则由该分布传递的信息量称为 P 的熵，记为

I (p) =-(i=1 to n 求和 ) piLog2(pi) 。
定义 3：若一个记录集合 T 根据类别属性的值被分成互相独立的类 C1C2..Ck，则识别 T 的一个元素所属哪个类所需要的信息量为 Info (T) =I (p) ，其中 P 为 C1C2 … Ck 的概率分布，即 P= (|C1|/|T| … |Ck|/|T|)

定义 4：若我们先根据非类别属性 X 的值将 T 分成集合 T1,T2 … Tn，则确定 T 中一个元素类的信息量可通过确定 Ti 的加权平均值来得到，即 Info(Ti) 的加权平均值为：

Info(X, T) = (i=1 to n 求和 ) ((|Ti|/|T |) Info (Ti))

定义 5：信息增益度是两个信息量之间的差值，其中一个信息量是需确定 T 的一个元素的信息量，另一个信息量是在已得到的属性 X 的值后需确定的 T 一个元素的信息量，信息增益度公式为：

Gain(X, T) =Info (T)-Info(X, T)

2.J48 即决策树 C4.5 算法

C4.5 算法一种分类决策树算法 , 其核心算法是 ID3 算法。C4.5 算法继承了 ID3 算法的优点，并在以下几方面对 ID3 算法进行了改进：

用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；

在树构造过程中进行剪枝；

能够完成对连续属性的离散化处理；

能够对不完整数据进行处理。

C4.5 算法有如下优点：产生的分类规则易于理解，准确率较高。其缺点是：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。

Rule

1.Decision Table 即决策表

决策表 (Decision Table)，是一中使用表的结构，精确而简洁描述复杂逻辑的方式。

2.JRip 即 RIPPER 算法

规则归纳学习从分类实例出发能够归纳出一般的概念描述。其中重要的算法为 IREP 算法和 RIPPER 算法。重复增量修枝（RIPPER）算法生成一条规则，随机地将没有覆盖的实例分成生长集合和修剪集合，规定规则集合中的每个规则是有两个规则来生成：替代规则和修订规则。

Meta

1.AdaBoostM1 即 AdaBoosting 算法

Adaboost 是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器 ( 弱分类器 ) ，然后把这些弱分类器集合起来，构成一个更强的最终分类器 ( 强分类器 ) 。其算法本身是通过改变数据分布来实现的，它根据每次训练集之中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器最后融合起来，作为最后的决策分类器。

2.Bagging 即 Bagging 方法

Bootstrps bagging boosting 都属于集成学习方法，将训练的学习器集成在一起。原理来源于 PAC 学习模型（Probably Approximately CorrectK）。其中的 Bagging 是 bootstrap aggregating 的缩写，是最早的 Ensemble 算法之一，它也是最直接容易实现，又具有不错的效果的算法之一。Bagging 中的多样性是由有放回抽取训练样本来实现的，用这种方式随机产生多个训练数据的子集，在每一个训练集的子集上训练一个同种分类器，最终分类结果是由多个分类器的分类结果多数投票而产生的。

Weka 中分类算法的参数解释

Correlation coefficient (= CC) ： 相关系数

Root mean squared error (= RMSE) ： 均方根误差

Root relative squared error (= RRSE) ： 相对平方根误差

Mean absolute error (= MAE) ： 平均绝对误差

Root absolute error (= RAE) ： 平均绝对误差平方根

Combined: (1-abs (CC)) + RRSE + RAE： 结合的

Accuracy (= ACC) ： 正确率

注意，Correction coefficient 只适用于连续值类别，Accuracy 只适用于离散类别

Kappa statistic：这个指标用于评判分类器的分类结果与随机分类的差异度。

绝对差值（Mean absolute error）：这个指标用于评判预测值与实际值之间的差异度。把多次测得值之间相互接近的程度称为精密度，精密度用偏差表示，偏差指测得值与平均值之间的差值，偏差越小，精密度则越高。

中误差（Root mean square error：RMSE）：带权残差平方和的平均数的平方根，作为在一定条件下衡量测量精度的一种数值指标。中误差是衡量观测精度的一种数字标准，亦称“标准差”或“均方根差”。在相同观测条件下的一组真误差平方中数的平方根。因真误差不易求得 , 所 以通常用最小二乘法求得的观测值改正数来代替真误差。它是观测值与真值偏差的平方和观测次数 n 比值的平方根。中误差不等于真误差，它仅是一组真误差的代表值。中误差的大小反映了该组观测值精度的高低，因此，通常称中误差为观测值的中误差。

分类算法的评价标准

预测的准确率：这涉及到模型正确地预测新的或先前没见过的数据的类 标号能力。

速度：涉及到产生和使用模型的计算花费。

强壮性：这涉及给定噪声数据或具有空缺值的数据，模型正确预测的能力。

可伸缩性：这涉及给定大量的数据，有效的构造模型的能力。

可解释性：这涉及学习模型提供的理解和洞察的层次。

分类算法的比较

以下主要采用两种数据集（Monk's Problems 和 Satimage）来分别运行不同的分类算法，采用的是 Weka 数据挖掘工具。

Monk's Problems 数据集特点

1. 属性全部为 nominal 类型

2. 训练样本较少

图 1. 训练数据集

3. 训练集数据的可视化图，该图根据直方图上方一栏所选择的 class 属性（attr6）来着色。

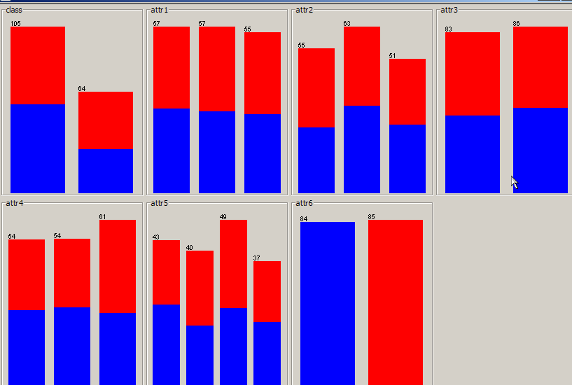
图 2. 训练数据集可视化图

各分类器初步分类效果分析

各分类器不做参数调整，使用默认参数进行得到的结果。

表 1. 分类器初步结果比较

分类器比较

预测的准确率比较

采用基于懒惰学习的 IB1、IBk 的分类器的误差率较低，采用基于概率统计的 BayesNet 分类器的误差率较高，其他的基于决策树和基于规则的分类器误差居于前两者之间，这是因为在样本较少的情况下，采用 IB1 时，生成的决策模型是在测试样本到来以后才生成，这样的学习模型可能更好的拟合局部的样本特性。采用统计学分类方法的 BayesNet 之所以准确度较低，可能是由于贝叶斯定理的成立本身需要很强的独立性假设前提，而此假设在实际情况中经常是不成立的。但是一般地，统计分类算法趋于计算量大。

进一步比较分类结果的散点图（其中正确分类的结果用叉表示，分错的结果用方框表示），发现 BayesNet 分类器针对属性 6（attr6）的预测结果分错的结果明显比 IB1 的分错结果要多些，而这些错误的散点中，又以属性 6 的取值为 2 的散点中错误的数目较多。

图 3. BayesNet 的分类结果散点图

图 4. IB1 分类结果散点图

分类速度比较

Adaboost 的分类花了 0.08 秒，Bagging 的分类花了 0.03 秒，相对于其他的分类器，这两个分类器速度较慢。这是因为这两个算法采用迭代，针对同一个训练集，训练多种分类器，然后把这些分类器集合起来，所以时间消耗较长。

分类器参数调优

IBK 调优

【 KNN 】：6

扩大邻近学习的节点范围，降低异常点的干扰（距离较大的异常点）

【 DistanceWeighting 】：Weight by 1/distance

通过修改距离权重，进一步降低异常点的干扰（距离较大的异常点）

图 5. IBk 分类调优

IBk 调优结果

调优后准确率从 60.65% 上升到 63.43%。

表 2. IBk 调优结果

J48 调优

【 binarySplits 】：True

采用 2 分法，生成决策树。

图 6. J48 分类调优

J48 调优结果

调优后准确率从 59.72% 上升到 64.35%，但是分类模型建立时间从 0 延长到了 0.31 秒

表 3. J48 调优结果

Salmage 数据集特点

1. 属性为 numeric 类型 , 共 37 个属性

2. 训练数据各类不平衡，测试数据各类不平衡

图 7. 训练数据集可视化图

各分类器初步分类效果分析

各分类器不做参数调整，使用默认参数得到的结果如下：

表 4. 分类器初步结果比较

分类器比较

预测的准确率比较

采用基于懒惰学习的 IB1、IBk 的分类器的准确率都较高，为 90.36%，采用 基于决策桩的 AdaBoostM 分类器的准确率较低，为 43.08%，贝叶斯分类器的准确 率较之前的数据集（Monk ’ s problem）有明显的提高，从 49% 到了 80% 左右，这主 要是因为样本空间的扩大，其他的分类器准确率也处于 80% 左右。

分类速度比较

DecisionTable 的分类花了 4.33 秒，Bagging 的分类花了 3.92 秒，J48 的分类模型建立花了 2.06 秒，相对于其他的分类器，这三个分类器速度较慢。

分类器参数调优

IBK 调优

【 KNN 】：6

扩大邻近学习的节点范围，降低异常点的干扰（距离较大的异常点）

【 DistanceWeighting 】：Weight by 1/distance

通过修改距离权重，进一步降低异常点的干扰（距离较大的异常点）

IBK 调优结果

调优后准确率从 90.36% 上升到 90.98%, 准确度有略微提升，说明通过扩大邻近学习的节点范围不能明显提高分类器的性能。

表 5. IBk 调优结果

J48 调优

【 binarySplits 】：True

采用 2 分法，生成决策树。

J48 调优结果

分类性能没有提升。说明采用 2 分法对分类没有影响。相反，时间比原来的算法有略微延长。

表 6. J48 调优结果

改进和建议

本文给出的调优方法只是一个简单的示例，实际上根据合理的参数调整，这些分类算法的效果还能得到更大的提升。