正交矩阵测试策略Orthogonal
Array Testing Strategy (OATS)
其实我本身没有负责这个项目的测试,不过是不想闲着所以拿这个做做玩玩:)有这样一个弹出窗口,上面有很多CheckBox,我只选了其中的7个作为例子的测试对象,意在举例子。

下表提取出需要测试的7个对象,他们分别有两种状态,要么被选中没有没有被选中:
| Quartiles |
Mean |
Median |
Std.Dev |
Min |
Skewness |
Kurtosis |
| YES |
YES |
YES |
YES |
YES |
YES |
YES |
| NO |
NO |
NO |
NO |
NO |
NO |
NO |
然后根据正交表进行映射,可以得到如下表,这个表有一部分是空的,那是因为用这8个case表示的两两组合已经是符合正交表的最低要求,就是两两组合至少出现一次,所以有这样子的空位出现
| case |
Quartiles |
Mean |
Median |
Std.Dev |
Min |
Skewness |
Kurtosis |
| 1 |
YES |
YES |
YES |
YES |
YES |
YES |
YES |
| 2 |
YES |
NO |
NO |
NO |
NO |
NO |
NO |
| 3 |
NO |
YES |
NO |
YES |
NO |
YES |
NO |
| 4 |
NO |
NO |
YES |
NO |
YES |
NO |
YES |
| 5 |
|
YES |
YES |
NO |
NO |
YES |
YES |
| 6 |
|
NO |
NO |
YES |
YES |
NO |
NO |
| 7 |
|
YES |
NO |
|
|
NO |
YES |
| 8 |
|
NO |
YES |
|
|
YES |
NO |
在处理这些空的数据格的时候我们可以根据一条原则进行处理,就是对那些敏感的区域或者是你觉得出现bug机会比较大的情况进行检验。例如下表,我假定Quartiles是选中的状态下有可能出现bug,所以我把这4个空全部填上了YES。对于后面那两个字段也是采用了同样的处理方法。就得出了下面这个表。
| case |
Quartiles |
Mean |
Median |
Std.Dev |
Min |
Skewness |
Kurtosis |
| 1 |
YES |
YES |
YES |
YES |
YES |
YES |
YES |
| 2 |
YES |
NO |
NO |
NO |
NO |
NO |
NO |
| 3 |
NO |
YES |
NO |
YES |
NO |
YES |
NO |
| 4 |
NO |
NO |
YES |
NO |
YES |
NO |
YES |
| 5 |
YES |
YES |
YES |
NO |
NO |
YES |
YES |
| 6 |
YES |
NO |
NO |
YES |
YES |
NO |
NO |
| 7 |
YES |
YES |
NO |
YES |
NO |
NO |
YES |
| 8 |
YES |
NO |
YES |
YES |
NO |
YES |
NO |
对于有7个字段,每个字段有2种可能的数值的情况,如果要做一个全面的测试,就需要2的7次方 128个Test
Case来做一个全面的覆盖,但是如果加上其他字段,或者某些字段的可选值是很多的(例如一个Text Box,用等价类划分了以后可能也有4~5种)。做一个全面的测试是不可能的。现在用8个测试用例来替代原来128个的方案,虽然肯定不能保证做到发现全部的bug,不过我个人觉得是一个“性价比”比较高的方案。
当然了,我们不能完全依靠正交表,如果不是我们本身的价值哪里去了,其实观察一下上面的表,很容易地发现了上面的表是没有全部NO的Test
Case的,所以我们可以根据自己的经验,认为全部都不选的情况是一个比较常见而且有肯能出错的情况,所以加上,然后还能加上一些在软件实际使用过程当中比较常用的组合还有容易出错的组合,来完成这个Test
Case计划。见下表,红色的就是后来加上去的。
| case |
Quartiles |
Mean |
Median |
Std.Dev |
Min |
Skewness |
Kurtosis |
| 1 |
YES |
YES |
YES |
YES |
YES |
YES |
YES |
| 2 |
YES |
NO |
NO |
NO |
NO |
NO |
NO |
| 3 |
NO |
YES |
NO |
YES |
NO |
YES |
NO |
| 4 |
NO |
NO |
YES |
NO |
YES |
NO |
YES |
| 5 |
YES |
YES |
YES |
NO |
NO |
YES |
YES |
| 6 |
YES |
NO |
NO |
YES |
YES |
NO |
NO |
| 7 |
YES |
YES |
NO |
YES |
NO |
NO |
YES |
| 8 |
YES |
NO |
YES |
YES |
NO |
YES |
NO |
| 9 |
NO |
NO |
NO |
NO |
NO |
NO |
NO |
| 10 |
NO |
NO |
YES |
YES |
YES |
YES |
NO |
这样子我就完成了一个10个Case的测试计划了。
回过头来看看正交矩阵测试策略Orthogonal Array Testing Strategy (OATS),OATS是一种对两两相互作用(pair-wise
interactions)进行系统的测试的一种方法,用正交表映射出来的测试用例大致上是均匀分布的。
正交矩阵(Orthogonal arrays)是一二维的矩阵,下面是一些关键字:
- Runs:就是矩阵的行数,也就是将来要映射的Test Case数。在这里例子里面是8。
- Factors:就是矩阵的列数,一般来说是有多少个变量,就有多少个Factor。这里例子就是7。
- Levels:就是取各列因素(Factors)中的最大可能取值。这个例子里面是2。
- Strength:相互关系数,这里面是2,意思就是每两个变量之间的关系,如果是3的话就意味着需要三个变量之间的组合,如果是这样的情况用例数会极速增加。
正交表通常的表达式是: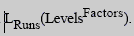
根据上面的数据可以查找到一些已经被证明是正确的正交表。可以参考这个地址:http://www.research.att.com/~njas/oadir/index.html
然后就能把正交表的01010101映射为我们的Case了!
后记:
1.为什么强调这个正交表是均匀分布的呢?从几何学角度来看软件的bug的话,bug可以分为两类,一种是范围性的错误(region
faults)另外一种是单独的错误(Single faults)。我们很难去估计在这个软件里面哪类错误存在于哪里,所以我们能做的就是取一个有限的集合去代替那个无限的集合。正因为如此,我们对这个有限的集合的要求就是尽可能地均匀分布的。
2.不要手工的实现正交表的映射。现在一般举例都是比较小规模的例子,一旦列变量很多很多,那就没有办法手工的去做映射的,需要借助工具~听说Excel可以做,我也正在研究,不过可以有其他选项~例如有个叫正交助手的软件,或者用SPSS……有点夸张。
3.滥用OATS。通常刚开始知道这个方法的时候就很有兴趣去弄他,然后就死也要实现这个方法,不过测试还是根据风险来决定测试的点。如果发现一个能应用OATS的地方,不过这个地方在整个软件里面占的比重并不是很大,或者说不是有很高优先级的,那么可以不用OATS。
4.用错了组合,其实就像是我举的这个例子,其实我没有读文档,也没有文档给我读,所以我并不知道那个界面上哪些东西是互相有影响的,所以我也只是随便挑出来罢了。做个例子可以,真正实施的时候要注意囖。
5.不要用OATS来测那些高风险的产品,例如什么医疗,银行的。
6.正交表只是取一个相对合理的集合作为全集合的一个代替,所以不要认为利用正交表就能替代原来的全集,用正交表是要承受风险的,但是正交表的确是一个“性价比”很高的方法:)有点像20/80法则,做20%的工作就得到了80%的效果:)
|