| 编辑推荐: |
本文来自csdn,本章讲解操作和处理图像的基础知识,将通过大量示例介绍处理图像所需的
Python 工具包,并介绍用于读取图像、图像转换和缩放、计算导数、画图和保存结果等的基本工具。这些工具的使用将贯穿本书的剩余章节。
|
|
第 1 章 基本的图像操作和处理
1.1 PIL:Python图像处理类库
PIL(Python Imaging Library Python,图像处理类库)提供了通用的图像处理功能,以及大量有用的基本图像操作,比如图像缩放、裁剪、旋转、颜色转换等。PIL
是免费的,可以从 下载。
利用 PIL 中的函数,我们可以从大多数图像格式的文件中读取数据,然后写入最常见的图像格式文件中。PIL
中最重要的模块为 Image。要读取一幅图像,可以使用:
from PIL import
Image
pil_im = Image.open('empire.jpg') |
上述代码的返回值 pil_im 是一个 PIL 图像对象。
图像的颜色转换可以使用 convert() 方法来实现。要读取一幅图像,并将其转换成灰度图像,只需要加上
convert('L'),如下所示:
| pil_im = Image.open('empire.jpg').convert('L') |
在 PIL 文档中有一些例子,参见 。这些例子的输出结果如图 1-1
所示。

图 1-1:用 PIL 处理图像的例子
1.1.1 转换图像格式
通过 save() 方法,PIL 可以将图像保存成多种格式的文件。下面的例子从文件名列表(filelist)中读取所有的图像文件,并转换成
JPEG 格式:
from PIL import
Image
import os
for infile in filelist:
outfile = os.path.splitext(infile)[0] + ".jpg"
if infile != outfile:
try:
Image.open(infile).save(outfile)
except IOError:
print "cannot convert", infile |
PIL 的 open() 函数用于创建 PIL 图像对象,save() 方法用于保存图像到具有指定文件名的文件。除了后缀变为“.jpg”,上述代码的新文件名和原文件名相同。PIL
是个足够智能的类库,可以根据文件扩展名来判定图像的格式。PIL 函数会进行简单的检查,如果文件不是
JPEG 格式,会自动将其转换成 JPEG 格式;如果转换失败,它会在控制台输出一条报告失败的消息。
本书会处理大量图像列表。下面将创建一个包含文件夹中所有图像文件的文件名列表。首先新建一个文件,命名为
imtools.py,来存储一些经常使用的图像操作,然后将下面的函数添加进去:
import os
def get_imlist(path):
""" 返回目录中所有JPG 图像的文件名列表"""
return [os.path.join(path,f) for f in os.listdir(path)
if f.endswith('.jpg')] |
现在,回到 PIL。
1.1.2 创建缩略图
使用 PIL 可以很方便地创建图像的缩略图。thumbnail()
方法接受一个元组参数(该参数指定生成缩略图的大小),然后将图像转换成符合元组参数指定大小的缩略图。例如,创建最长边为
128 像素的缩略图,可以使用下列命令:
| pil_im.thumbnail((128,128)) |
1.1.3 复制和粘贴图像区域
使用 crop() 方法可以从一幅图像中裁剪指定区域:
box = (100,100,400,400)
region = pil_im.crop(box) |
该区域使用四元组来指定。四元组的坐标依次是(左,上,右,下)。PIL
中指定坐标系的左上角坐标为(0,0)。我们可以旋转上面代码中获取的区域,然后使用 paste() 方法将该区域放回去,具体实现如下:
region = region.transpose(Image.ROTATE_180)
pil_im.paste(region,box) |
1.1.4 调整尺寸和旋转
要调整一幅图像的尺寸,我们可以调用 resize() 方法。该方法的参数是一个元组,用来指定新图像的大小:
| out = pil_im.resize((128,128)) |
要旋转一幅图像,可以使用逆时针方式表示旋转角度,然后调用 rotate()
方法:
上述例子的输出结果如图 1-1 所示。最左端是原始图像,然后是灰度图像、粘贴有旋转后裁剪图像的原始图像,最后是缩略图。
1.2 Matplotlib
我们处理数学运算、绘制图表,或者在图像上绘制点、直线和曲线时,Matplotlib
是个很好的类库,具有比 PIL 更强大的绘图功能。Matplotlib 可以绘制出高质量的图表,就像本书中的许多插图一样。Matplotlib
中的 PyLab 接口包含很多方便用户创建图像的函数。Matplotlib 是开源工具,可以从 免费下载。该链接中包含非常详尽的使用说明和教程。下面的例子展示了本书中需要使用的大部分函数。
1.2.1 绘制图像、点和线
尽管 Matplotlib 可以绘制出较好的条形图、饼状图、散点图等,但是对于大多数计算机视觉应用来说,仅仅需要用到几个绘图命令。最重要的是,我们想用点和线来表示一些事物,比如兴趣点、对应点以及检测出的物体。下面是用几个点和一条线绘制图像的例子:
from PIL import Image
from pylab import *
# 读取图像到数组中
im = array(Image.open('empire.jpg'))
# 绘制图像
imshow(im)
# 一些点
x = [100,100,400,400]
y = [200,500,200,500]
# 使用红色星状标记绘制点
plot(x,y,'r*')
# 绘制连接前两个点的线
plot(x[:2],y[:2])
# 添加标题,显示绘制的图像
title('Plotting: "empire.jpg"')
show() |
上面的代码首先绘制出原始图像,然后在 x 和 y 列表中给定点的 x 坐标和 y 坐标上绘制出红色星状标记点,最后在两个列表表示的前两个点之间绘制一条线段(默认为蓝色)。该例子的绘制结果如图
1-2 所示。show() 命令首先打开图形用户界面(GUI),然后新建一个图像窗口。该图形用户界面会循环阻断脚本,然后暂停,直到最后一个图像窗口关闭。在每个脚本里,你只能调用一次
show() 命令,而且通常是在脚本的结尾调用。注意,在 PyLab 库中,我们约定图像的左上角为坐标原点。
图像的坐标轴是一个很有用的调试工具;但是,如果你想绘制出较美观的图像,加上下列命令可以使坐标轴不显示:
上面的命令将绘制出如图 1-2 右边所示的图像。

图 1-2:Matplotlib 绘图示例。带有坐标轴和不带坐标轴的包含点和一条线段的图像
在绘图时,有很多选项可以控制图像的颜色和样式。最有用的一些短命令如表
1-1、表 1-2 和表 1-3 所示。使用方法见下面的例子:
plot(x,y) # 默认为蓝色实线
plot(x,y,'r*') # 红色星状标记
plot(x,y,'go-') # 带有圆圈标记的绿线
plot(x,y,'ks:') # 带有正方形标记的黑色虚线 |
表1-1:用PyLab库绘图的基本颜色格式命令
|
颜色 |
|
'b' |
蓝色 |
|
'g' |
绿色 |
|
'r' |
红色 |
|
'c' |
青色 |
|
'm' |
品红 |
|
'y' |
黄色 |
|
'k' |
黑色 |
|
'w' |
白色 |
表1-2:用PyLab库绘图的基本线型格式命令
表1-3:用PyLab库绘图的基本绘制标记格式命令
|
标记 |
|
'.' |
点 |
|
'o' |
圆圈 |
|
's' |
正方形 |
|
'*' |
星形 |
|
'+' |
加号 |
|
'x' |
叉号 |
1.2.2 图像轮廓和直方图
下面来看两个特别的绘图示例:图像的轮廓和直方图。绘制图像的轮廓(或者其他二维函数的等轮廓线)在工作中非常有用。因为绘制轮廓需要对每个坐标
[x, y] 的像素值施加同一个阈值,所以首先需要将图像灰度化:
from PIL import
Image
from pylab import *
# 读取图像到数组中
im = array(Image.open('empire.jpg').convert('L'))
# 新建一个图像
figure()
# 不使用颜色信息
gray()
# 在原点的左上角显示轮廓图像
contour(im, origin='image')
axis('equal')
axis('off') |
像之前的例子一样,这里用 PIL 的 convert() 方法将图像转换成灰度图像。
图像的直方图用来表征该图像像素值的分布情况。用一定数目的小区间(bin)来指定表征像素值的范围,每个小区间会得到落入该小区间表示范围的像素数目。该(灰度)图像的直方图可以使用
hist() 函数绘制:
figure()
hist(im.flatten(),128)
show() |
hist() 函数的第二个参数指定小区间的数目。需要注意的是,因为 hist() 只接受一维数组作为输入,所以我们在绘制图像直方图之前,必须先对图像进行压平处理。flatten()
方法将任意数组按照行优先准则转换成一维数组。图 1-3 为等轮廓线和直方图图像。
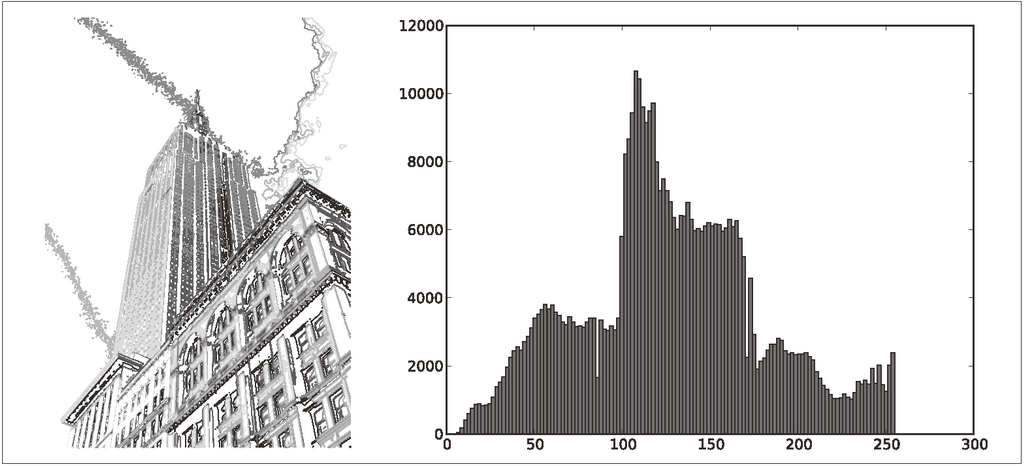
图 1-3:用 Matplotlib 绘制图像等轮廓线和直方图
1.2.3 交互式标注
有时用户需要和某些应用交互,例如在一幅图像中标记一些点,或者标注一些训练数据。PyLab
库中的 ginput() 函数就可以实现交互式标注。下面是一个简短的例子:
from PIL import Image
from pylab import *
im = array(Image.open('empire.jpg'))
imshow(im)
print 'Please click 3 points'
x = ginput(3)
print 'you clicked:',x
show() |
上面的脚本首先绘制一幅图像,然后等待用户在绘图窗口的图像区域点击三次。程序将这些点击的坐标 [x,
y] 自动保存在 x 列表里。
1.3 NumPy
NumPy是非常有名的 Python 科学计算工具包,其中包含了大量有用的思想,比如数组对象(用来表示向量、矩阵、图像等)以及线性代数函数。NumPy
中的数组对象几乎贯穿用于本书的所有例子中 1 数组对象可以帮助你实现数组中重要的操作,比如矩阵乘积、转置、解方程系统、向量乘积和归一化,这为图像变形、对变化进行建模、图像分类、图像聚类等提供了基础。
1PyLab 实际上包含 NumPy 的一些内容,如数组类型。这也是我们能够在 1.2 节使用数组类型的原因。
NumPy
可以从 免费下载,在线说明文档包含了你可能遇到的大多数问题的答案。关于
NumPy 的更多内容,请参考开源书籍 [24]。
1.3.1 图像数组表示
在先前的例子中,当载入图像时,我们通过调用 array() 方法将图像转换成 NumPy 的数组对象,但当时并没有进行详细介绍。NumPy
中的数组对象是多维的,可以用来表示向量、矩阵和图像。一个数组对象很像一个列表(或者是列表的列表),但是数组中所有的元素必须具有相同的数据类型。除非创建数组对象时指定数据类型,否则数据类型会按照数据的类型自动确定。
对于图像数据,下面的例子阐述了这一点:
im = array(Image.open('empire.jpg'))
print im.shape, im.dtype
im = array(Image.open('empire.jpg').convert('L'),'f')
print im.shape, im.dtype
|
控制台输出结果如下所示:
(800, 569, 3)
uint8
(800, 569) float32
|
每行的第一个元组表示图像数组的大小(行、列、颜色通道),紧接着的字符串表示数组元素的数据类型。因为图像通常被编码成无符号八位整数(uint8),所以在第一种情况下,载入图像并将其转换到数组中,数组的数据类型为“uint8”。在第二种情况下,对图像进行灰度化处理,并且在创建数组时使用额外的参数“f”;该参数将数据类型转换为浮点型。关于更多数据类型选项,可以参考图书
[24]。注意,由于灰度图像没有颜色信息,所以在形状元组中,它只有两个数值。
数组中的元素可以使用下标访问。位于坐标 i、j,以及颜色通道 k 的像素值可以像下面这样访问:
多个数组元素可以使用数组切片方式访问。切片方式返回的是以指定间隔下标访问该数组的元素值。下面是有关灰度图像的一些例子:
im[i,:] = im[j,:] # 将第 j 行的数值赋值给第 i 行
im[:,i] = 100 # 将第 i 列的所有数值设为100
im[:100,:50].sum() # 计算前100 行、前 50 列所有数值的和
im[50:100,50:100] # 50~100 行,50~100 列(不包括第 100
行和第 100 列)
im[i].mean() # 第 i 行所有数值的平均值
im[:,-1] # 最后一列
im[-2,:] (or im[-2]) # 倒数第二行 |
注意,示例仅仅使用一个下标访问数组。如果仅使用一个下标,则该下标为行下标。注意,在最后几个例子中,负数切片表示从最后一个元素逆向计数。我们将会频繁地使用切片技术访问像素值,这也是一个很重要的思想。
我们有很多操作和方法来处理数组对象。本书将在使用到的地方逐一介绍。你可以查阅在线文档或者开源图书
[24] 获取更多信息。
1.3.2 灰度变换
将图像读入 NumPy 数组对象后,我们可以对它们执行任意数学操作。一个简单的例子就是图像的灰度变换。考虑任意函数
f,它将 0...255 区间(或者 0...1 区间)映射到自身(意思是说,输出区间的范围和输入区间的范围相同)。下面是关于灰度变换的一些例子:
from PIL import Image
from numpy import *
im = array(Image.open('empire.jpg').convert('L'))
im2 = 255 - im # 对图像进行反相处理
im3 = (100.0/255) * im + 100 # 将图像像素值变换到100...200
区间
im4 = 255.0 * (im/255.0)**2 # 对图像像素值求平方后得到的图像 |
第一个例子将灰度图像进行反相处理;第二个例子将图像的像素值变换到
100...200 区间;第三个例子对图像使用二次函数变换,使较暗的像素值变得更小。图 1-4 为所使用的变换函数图像。图
1-5 是输出的图像结果。你可以使用下面的命令查看图像中的最小和最大像素值:
| print int(im.min()),
int(im.max()) |
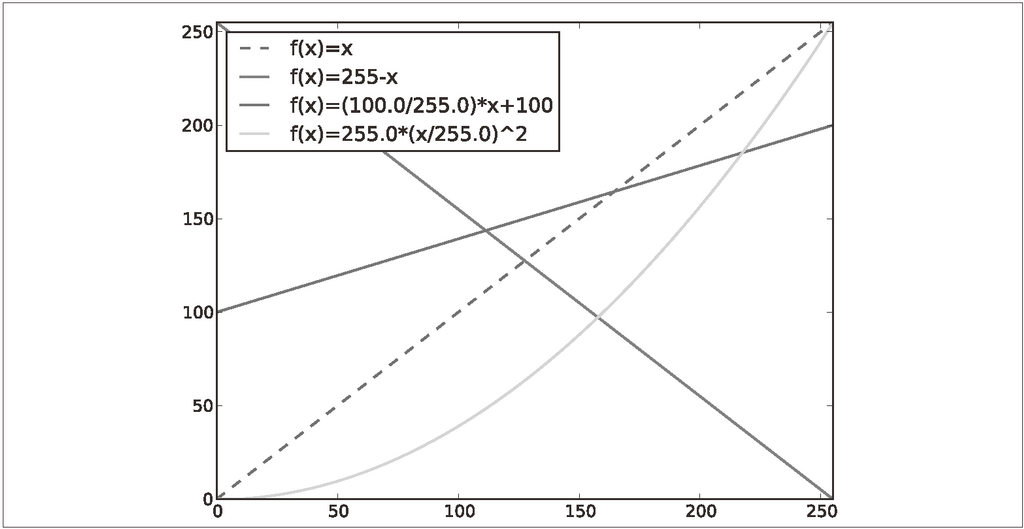
图 1-4:灰度变换示例。三个例子中所使用函数的图像,其中虚线表示恒等变换

图 1-5:灰度变换。对图像应用图 1-4 中的函数:f(x)=255-x 对图像进行反相处理(左);f(x)=(100/255)x+100
对图像进行变换(中);f(x)=255(x/255)2 对图像做二次变换(右)
如果试着对上面例子查看最小值和最大值,可以得到下面的输出结果:
2 255
0 253
100 200
0 255 |
array() 变换的相反操作可以使用 PIL 的 fromarray()
函数完成:
| pil_im = Image.fromarray(im) |
如果你通过一些操作将“uint8”数据类型转换为其他数据类型,比如之前例子中的
im3 或者 im4,那么在创建 PIL 图像之前,需要将数据类型转换回来:
| pil_im = Image.fromarray(uint8(im)) |
如果你并不十分确定输入数据的类型,安全起见,应该先转换回来。注意,NumPy 总是将数组数据类型转换成能够表示数据的“最低”数据类型。对浮点数做乘积或除法操作会使整数类型的数组变成浮点类型。
1.3.3 图像缩放
NumPy 的数组对象是我们处理图像和数据的主要工具。想要对图像进行缩放处理没有现成简单的方法。我们可以使用之前
PIL 对图像对象转换的操作,写一个简单的用于图像缩放的函数。把下面的函数添加到 imtool.py
文件里:
def imresize(im,sz):
""" 使用PIL 对象重新定义图像数组的大小"""
pil_im = Image.fromarray(uint8(im))
return array(pil_im.resize(sz)) |
我们将会在接下来的内容中使用这个函数。
1.3.4 直方图均衡化
图像灰度变换中一个非常有用的例子就是直方图均衡化。直方图均衡化是指将一幅图像的灰度直方图变平,使变换后的图像中每个灰度值的分布概率都相同。在对图像做进一步处理之前,直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法,并且可以增强图像的对比度。
在这种情况下,直方图均衡化的变换函数是图像中像素值的累积分布函数(cumulative distribution
function,简写为 cdf,将像素值的范围映射到目标范围的归一化操作)。
下面的函数是直方图均衡化的具体实现。将这个函数添加到 imtool.py
里:
def histeq(im,nbr_bins=256):
""" 对一幅灰度图像进行直方图均衡化"""
# 计算图像的直方图
imhist,bins = histogram(im.flatten(),nbr_bins,normed=True)
cdf = imhist.cumsum() # cumulative distribution
function
cdf = 255 * cdf / cdf[-1] # 归一化
# 使用累积分布函数的线性插值,计算新的像素值
im2 = interp(im.flatten(),bins[:-1],cdf)
return im2.reshape(im.shape), cdf |
该函数有两个输入参数,一个是灰度图像,一个是直方图中使用小区间的数目。函数返回直方图均衡化后的图像,以及用来做像素值映射的累积分布函数。注意,函数中使用到累积分布函数的最后一个元素(下标为
-1),目的是将其归一化到 0...1 范围。你可以像下面这样使用该函数:
from PIL import Image
from numpy import *
im = array(Image.open('AquaTermi_lowcontrast.jpg').convert('L'))
im2,cdf = imtools.histeq(im) |
图 1-6 和图 1-7 为上面直方图均衡化例子的结果。上面一行显示的分别是直方图均衡化之前和之后的灰度直方图,以及累积概率分布函数映射图像。可以看到,直方图均衡化后图像的对比度增强了,原先图像灰色区域的细节变得清晰。
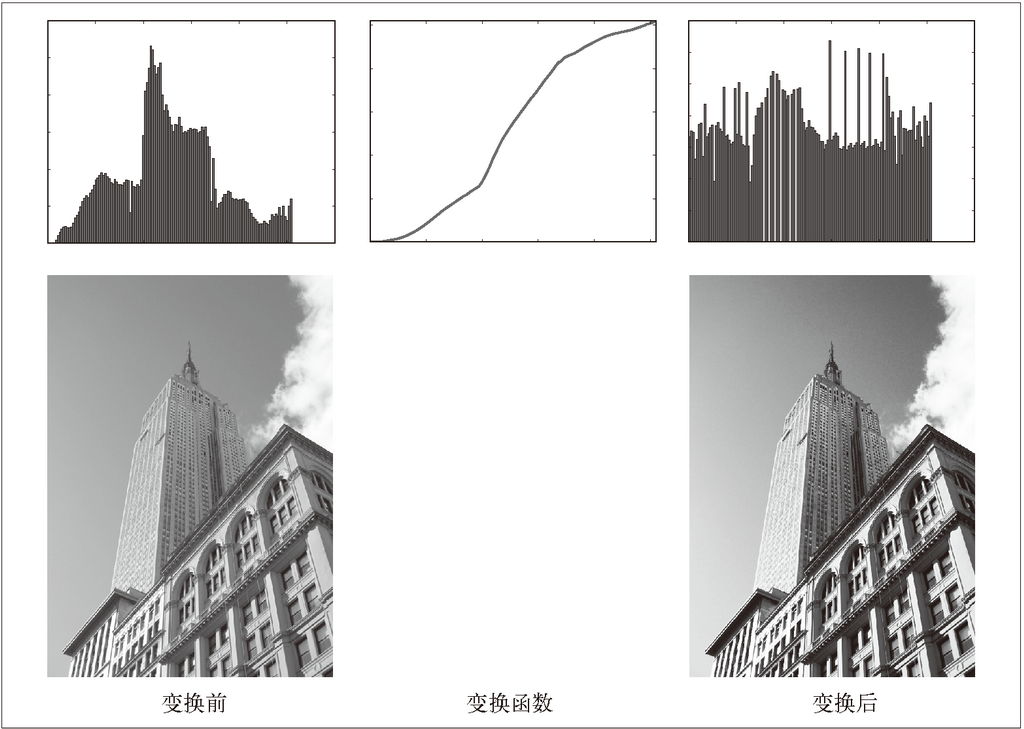
图 1-6:直方图均衡化示例。左侧为原始图像和直方图,中间图为灰度变换函数,右侧为直方图均衡化后的图像和相应直方图
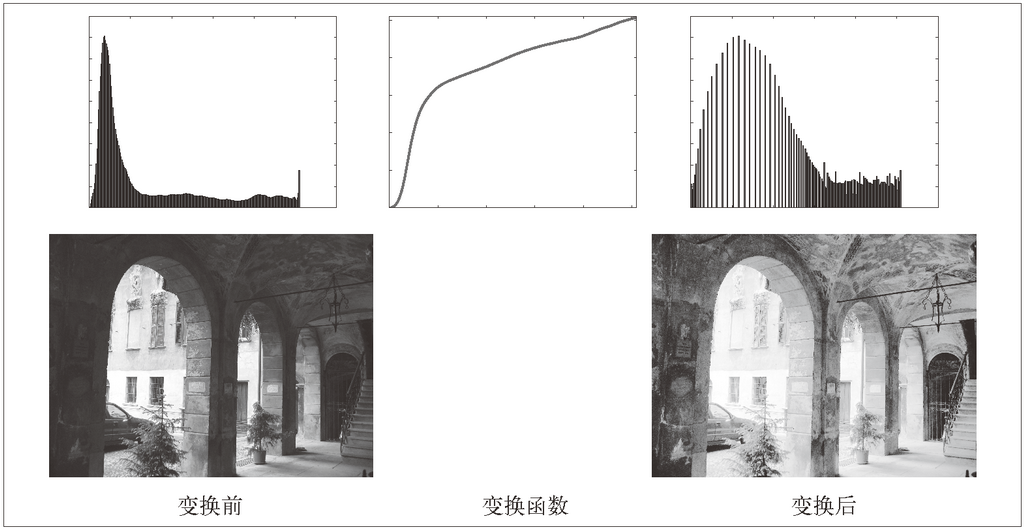
图 1-7:直方图均衡化示例。左侧为原始图像和直方图,中间图为灰度变换函数,右侧为直方图均衡化后的图像和相应直方图
1.3.5 图像平均
图像平均操作是减少图像噪声的一种简单方式,通常用于艺术特效。我们可以简单地从图像列表中计算出一幅平均图像。假设所有的图像具有相同的大小,我们可以将这些图像简单地相加,然后除以图像的数目,来计算平均图像。下面的函数可以用于计算平均图像,将其添加到
imtool.py 文件里:
def compute_average(imlist):
"""
计算图像列表的平均图像"""
# 打开第一幅图像,将其存储在浮点型数组中
averageim = array(Image.open(imlist[0]), 'f')
for imname in imlist[1:]:
try:
averageim += array(Image.open(imname))
except:
print imname + '...skipped'
averageim /= len(imlist)
# 返回uint8 类型的平均图像
return array(averageim, 'uint8') |
该函数包括一些基本的异常处理技巧,可以自动跳过不能打开的图像。我们还可以使用 mean() 函数计算平均图像。mean()
函数需要将所有的图像堆积到一个数组中;也就是说,如果有很多图像,该处理方式需要占用很多内存。我们将会在下一节中使用该函数。
1.3.6 图像的主成分分析(PCA)
PCA(Principal Component Analysis,主成分分析)是一个非常有用的降维技巧。它可以在使用尽可能少维数的前提下,尽量多地保持训练数据的信息,在此意义上是一个最佳技巧。即使是一幅
100×100 像素的小灰度图像,也有 10 000 维,可以看成 10 000 维空间中的一个点。一兆像素的图像具有百万维。由于图像具有很高的维数,在许多计算机视觉应用中,我们经常使用降维操作。PCA
产生的投影矩阵可以被视为将原始坐标变换到现有的坐标系,坐标系中的各个坐标按照重要性递减排列。
为了对图像数据进行 PCA 变换,图像需要转换成一维向量表示。我们可以使用 NumPy 类库中的
flatten() 方法进行变换。
将变平的图像堆积起来,我们可以得到一个矩阵,矩阵的一行表示一幅图像。在计算主方向之前,所有的行图像按照平均图像进行了中心化。我们通常使用
SVD(Singular Value Decomposition,奇异值分解)方法来计算主成分;但当矩阵的维数很大时,SVD
的计算非常慢,所以此时通常不使用 SVD 分解。下面就是 PCA 操作的代码:
from PIL import
Image
from numpy import *
def pca(X):
""" 主成分分析:
输入:矩阵X ,其中该矩阵中存储训练数据,每一行为一条训练数据
返回:投影矩阵(按照维度的重要性排序)、方差和均值"""
# 获取维数
num_data,dim = X.shape
# 数据中心化
mean_X = X.mean(axis=0)
X = X - mean_X
if dim>num_data:
# PCA- 使用紧致技巧
M = dot(X,X.T) # 协方差矩阵
e,EV = linalg.eigh(M) # 特征值和特征向量
tmp = dot(X.T,EV).T # 这就是紧致技巧
V = tmp[::-1] # 由于最后的特征向量是我们所需要的,所以需要将其逆转
S = sqrt(e)[::-1] # 由于特征值是按照递增顺序排列的,所以需要将其逆转
for i in range(V.shape[1]):
V[:,i] /= S
else:
# PCA- 使用SVD 方法
U,S,V = linalg.svd(X)
V = V[:num_data] # 仅仅返回前nun_data 维的数据才合理
# 返回投影矩阵、方差和均值
return V,S,mean_X
|
该函数首先通过减去每一维的均值将数据中心化,然后计算协方差矩阵对应最大特征值的特征向量,此时可以使用简明的技巧或者
SVD 分解。这里我们使用了 range() 函数,该函数的输入参数为一个整数 n,函数返回整数 0...(n-1)
的一个列表。你也可以使用 arange() 函数来返回一个数组,或者使用 xrange() 函数返回一个产生器(可能会提升速度)。我们在本书中贯穿使用
range() 函数。
如果数据个数小于向量的维数,我们不用 SVD 分解,而是计算维数更小的协方差矩阵 XXT 的特征向量。通过仅计算对应前
k(k 是降维后的维数)最大特征值的特征向量,可以使上面的 PCA 操作更快。由于篇幅所限,有兴趣的读者可以自行探索。矩阵
V 的每行向量都是正交的,并且包含了训练数据方差依次减少的坐标方向。
我们接下来对字体图像进行 PCA 变换。fontimages.zip 文件包含采用不同字体的字符
a 的缩略图。所有的 2359 种字体可以免费下载 2。假定这些图像的名称保存在列表 imlist
中,跟之前的代码一起保存传在 pca.py 文件中,我们可以使用下面的脚本计算图像的主成分:
2免费字体图像库由 Martin Solli 收集并上传(http://webstaff.itn.liu.se/~marso/)。
from PIL import Image
from numpy import *
from pylab import *
import pca
im = array(Image.open(imlist[0])) # 打开一幅图像,获取其大小
m,n = im.shape[0:2] # 获取图像的大小
imnbr = len(imlist) # 获取图像的数目
# 创建矩阵,保存所有压平后的图像数据
immatrix = array([array(Image.open(im)).flatten()
for im in imlist],'f')
# 执行 PCA 操作
V,S,immean = pca.pca(immatrix)
# 显示一些图像(均值图像和前 7 个模式)
figure()
gray()
subplot(2,4,1)
imshow(immean.reshape(m,n))
for i in range(7):
subplot(2,4,i+2)
imshow(V[i].reshape(m,n))
|
注意,图像需要从一维表示重新转换成二维图像;可以使用 reshape() 函数。如图 1-8 所示,运行该例子会在一个绘图窗口中显示
8 个图像。这里我们使用了 PyLab 库的 subplot() 函数在一个窗口中放置多个图像。

图 1-8:平均图像(左上)和前 7 个模式(具有最大方差的方向模式)
1.3.7 使用pickle模块
如果想要保存一些结果或者数据以方便后续使用,Python 中的 pickle 模块非常有用。pickle
模块可以接受几乎所有的 Python 对象,并且将其转换成字符串表示,该过程叫做封装(pickling)。从字符串表示中重构该对象,称为拆封(unpickling)。这些字符串表示可以方便地存储和传输。
我们来看一个例子。假设想要保存上一节字体图像的平均图像和主成分,可以这样来完成:
# 保存均值和主成分数据
f = open('font_pca_modes.pkl', 'wb')
pickle.dump(immean,f)
pickle.dump(V,f)
f.close() |
在上述例子中,许多对象可以保存到同一个文件中。pickle 模块中有很多不同的协议可以生成
.pkl 文件;如果不确定的话,最好以二进制文件的形式读取和写入。在其他 Python 会话中载入数据,只需要如下使用
load() 方法:
# 载入均值和主成分数据
f = open('font_pca_modes.pkl', 'rb')
immean = pickle.load(f)
V = pickle.load(f)
f.close() |
注意,载入对象的顺序必须和先前保存的一样。Python 中有个用
C 语言写的优化版本,叫做 cpickle 模块,该模块和标准 pickle 模块完全兼容。关于 pickle
模块的更多内容,参见
pickle 模块文档页 。
在本书接下来的章节中,我们将使用 with 语句处理文件的读写操作。这是
Python 2.5 引入的思想,可以自动打开和关闭文件(即使在文件打开时发生错误)。下面的例子使用
with() 来实现保存和载入操作:
# 打开文件并保存
with open('font_pca_modes.pkl', 'wb') as f:
pickle.dump(immean,f)
pickle.dump(V,f) |
和
# 打开文件并载入
with open('font_pca_modes.pkl', 'rb') as f:
immean = pickle.load(f)
V = pickle.load(f) |
上面的例子乍看起来可能很奇怪,但 with() 确实是个很有用的思想。如果你不喜欢它,可以使用之前的
open 和 close函数。
作为 pickle 的一种替代方式,NumPy 具有读写文本文件的简单函数。如果数据中不包含复杂的数据结构,比如在一幅图像上点击的点列表,NumPy
的读写函数会很有用。保存一个数组 x 到文件中,可以使用:
| savetxt('test.txt',x,'%i') |
最后一个参数表示应该使用整数格式。类似地,读取可以使用:
你可以从在线文档
了解更多内容。
最后,NumPy 有专门用于保存和载入数组的函数。你可以在上面的在线文档里查看关于 save()
和 load() 的更多内容。
1.4 SciPy
SciPy 是建立在 NumPy 基础上,用于数值运算的开源工具包。SciPy
提供很多高效的操作,可以实现数值积分、优化、统计、信号处理,以及对我们来说最重要的图像处理功能。接下来,本节会介绍
SciPy 中大量有用的模块。SciPy 是个开源工具包.
下载。
1.4.1 图像模糊
图像的高斯模糊是非常经典的图像卷积例子。本质上,图像模糊就是将(灰度)图像 I 和一个高斯核进行卷积操作:
Iσ = I*Gσ
其中 * 表示卷积操作;Gσ 是标准差为 σ 的二维高斯核,定义为 :
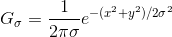
高斯模糊通常是其他图像处理操作的一部分,比如图像插值操作、兴趣点计算以及很多其他应用。
SciPy 有用来做滤波操作的 scipy.ndimage.filters
模块。该模块使用快速一维分离的方式来计算卷积。你可以像下面这样来使用它:
from PIL import
Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('empire.jpg').convert('L'))
im2 = filters.gaussian_filter(im,5) |
上面 guassian_filter() 函数的最后一个参数表示标准差。
图 1-9 显示了随着 σ 的增加,一幅图像被模糊的程度。σ 越大,处理后的图像细节丢失越多。如果打算模糊一幅彩色图像,只需简单地对每一个颜色通道进行高斯模糊:
im = array(Image.open('empire.jpg'))
im2 = zeros(im.shape)
for i in range(3):
im2[:,:,i] = filters.gaussian_filter(im[:,:,i],5)
im2 = uint8(im2) |
在上面的脚本中,最后并不总是需要将图像转换成 uint8 格式,这里只是将像素值用八位来表示。我们也可以使用:
来完成转换。
关于该模块更多的内容以及不同参数的选择,请查看
上 SciPy 文档中的 scipy.ndimage 部分。
图 1-9:使用 scipy.ndimage.filters 模块进行高斯模糊:(a)原始灰度图像;(b)使用
σ=2 的高斯滤波器;(c)使用 σ=5 的高斯滤波器;(d)使用 σ=10 的高斯滤波器
1.4.2 图像导数
整本书中可以看到,在很多应用中图像强度的变化情况是非常重要的信息。强度的变化可以用灰度图像 I(对于彩色图像,通常对每个颜色通道分别计算导数)的
x 和 y 方向导数 Ix 和 Iy 进行描述。
图像的梯度向量为▽I = [Ix, Iy]T。梯度有两个重要的属性,一是梯度的大小:
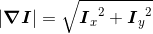
它描述了图像强度变化的强弱,一是梯度的角度:
α=arctan2(Iy, Ix)
描述了图像中在每个点(像素)上强度变化最大的方向。NumPy 中的 arctan2() 函数返回弧度表示的有符号角度,角度的变化区间为
-π...π。
我们可以用离散近似的方式来计算图像的导数。图像导数大多数可以通过卷积简单地实现:

对于 Dx 和 Dy,通常选择 Prewitt 滤波器:
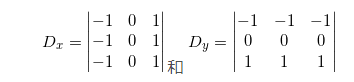
或者 Sobel 滤波器:
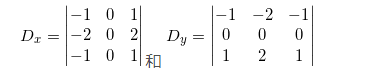
这些导数滤波器可以使用 scipy.ndimage.filters
模块的标准卷积操作来简单地实现,例如:
from PIL import Image
from numpy import *
from scipy.ndimage import filters
im = array(Image.open('empire.jpg').convert('L'))
# Sobel 导数滤波器
imx = zeros(im.shape)
filters.sobel(im,1,imx)
imy = zeros(im.shape)
filters.sobel(im,0,imy)
magnitude = sqrt(imx**2+imy**2) |
上面的脚本使用 Sobel 滤波器来计算 x 和 y 的方向导数,以及梯度大小。sobel() 函数的第二个参数表示选择
x 或者 y 方向导数,第三个参数保存输出的变量。图 1-10 显示了用 Sobel 滤波器计算出的导数图像。在两个导数图像中,正导数显示为亮的像素,负导数显示为暗的像素。灰色区域表示导数的值接近于零。

图 1-10:使用 Sobel 导数滤波器计算导数图像:(a)原始灰度图像;(b)x 导数图像;(c)y
导数图像;(d)梯度大小图像
上述计算图像导数的方法有一些缺陷:在该方法中,滤波器的尺度需要随着图像分辨率的变化而变化。为了在图像噪声方面更稳健,以及在任意尺度上计算导数,我们可以使用高斯导数滤波器:

其中,Gσx和 Gσy 表示 Gσ 在 x 和 y 方向上的导数,Gσ 为标准差为 σ 的高斯函数。
我们之前用于模糊的 filters.gaussian_filter()
函数可以接受额外的参数,用来计算高斯导数。可以简单地按照下面的方式来处理:
sigma = 5 # 标准差
imx = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (0,1),
imx)
imy = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (1,0),
imy) |
该函数的第三个参数指定对每个方向计算哪种类型的导数,第二个参数为使用的标准差。你可以查看相应文档了解详情。图
1-11 显示了不同尺度下的导数图像和梯度大小。你可以和图 1-9 中做相同尺度模糊的图像做比较。

图 1-11:使用高斯导数计算图像导数:x 导数图像(上),y 导数图像(中),以及梯度大小图像(下);(a)为原始灰度图像,(b)为使用
σ=2 的高斯导数滤波器处理后的图像,(c)为使 用 σ=5 的高斯导数滤波器处理后的图像,(d)为使用
σ=10 的高斯导数滤波器处理后的图像
1.4.3 形态学:对象计数
形态学(或数学形态学)是度量和分析基本形状的图像处理方法的基本框架与集合。形态学通常用于处理二值图像,但是也能够用于灰度图像。二值图像是指图像的每个像素只能取两个值,通常是
0 和 1。二值图像通常是,在计算物体的数目,或者度量其大小时,对一幅图像进行阈值化后的结果。你可以从
大体了解形态学及其处理图像的方式。
scipy.ndimage 中的 morphology 模块可以实现形态学操作。你可以使用 scipy.ndimage
中的 measurements 模块来实现二值图像的计数和度量功能。下面通过一个简单的例子介绍如何使用它们。
考虑在图 1-12a3 里的二值图像,计算该图像中的对象个数可以通过下面的脚本实现:
3这个图像实际上是图像“分割”后的结果。如果你想知道该图像是如何创建的,可以查看
9.3 节。
from scipy.ndimage import measurements,morphology
# 载入图像,然后使用阈值化操作,以保证处理的图像为二值图像
im = array(Image.open('houses.png').convert('L'))
im = 1*(im<128)
labels, nbr_objects = measurements.label(im)
print "Number of objects:", nbr_objects |
上面的脚本首先载入该图像,通过阈值化方式来确保该图像是二值图像。通过和
1 相乘,脚本将布尔数组转换成二进制表示。然后,我们使用 label() 函数寻找单个的物体,并且按照它们属于哪个对象将整数标签给像素赋值。图
1-12b 是labels 数组的图像。图像的灰度值表示对象的标签。可以看到,在一些对象之间有一些小的连接。进行二进制开(binary
open)操作,我们可以将其移除:
# 形态学开操作更好地分离各个对象
im_open = morphology.binary_opening(im,ones((9,5)),iterations=2)
labels_open, nbr_objects_open = measurements.label(im_open)
print "Number of objects:", nbr_objects_open
|
binary_opening() 函数的第二个参数指定一个数组结构元素。该数组表示以一个像素为中心时,使用哪些相邻像素。在这种情况下,我们在
y 方向上使用 9 个像素(上面 4 个像素、像素本身、下面 4 个像素),在 x 方向上使用 5
个像素。你可以指定任意数组为结构元素,数组中的非零元素决定使用哪些相邻像素。参数 iterations
决定执行该操作的次数。你可以尝试使用不同的迭代次数 iterations 值,看一下对象的数目如何变化。你可以在图
1-12c 与图 1-12d 中查看经过开操作后的图像,以及相应的标签图像。正如你想象的一样,binary_closing()
函数实现相反的操作。我们将该函数和在morphology 和 measurements 模块中的其他函数的用法留作练习。你可以从
scipy.ndimage 模块文档
中了解关于这些函数的更多知识。

图 1-12:形态学示例。使用二值开操作将对象分开,然后计算物体的数目:(a)为原始二值图像;(b)为对应原始图像的标签图像,其中灰度值表示物体的标签;(c)为使用开操作后的二值图像;(d)为开操作后图像的标签图像
1.4.4 一些有用的SciPy模块
SciPy 中包含一些用于输入和输出的实用模块。下面介绍其中两个模块:io 和 misc。
读写.mat文件
如果你有一些数据,或者在网上下载到一些有趣的数据集,这些数据以 Matlab
的 .mat 文件格式存储,那么可以使用 scipy.io 模块进行读取。
| data = scipy.io.loadmat('test.mat') |
上面代码中,data 对象包含一个字典,字典中的键对应于保存在原始
.mat 文件中的变量名。由于这些变量是数组格式的,因此可以很方便地保存到 .mat 文件中。你仅需创建一个字典(其中要包含你想要保存的所有变量),然后使用
savemat() 函数:
data = {}
data['x'] = x
scipy.io.savemat('test.mat',data) |
因为上面的脚本保存的是数组 x,所以当读入到 Matlab 中时,变量的名字仍为 x。关于 scipy.io
模块的更多内容,请参见在线文档 。
以图像形式保存数组
因为我们需要对图像进行操作,并且需要使用数组对象来做运算,所以将数组直接保存为图像文件 4 非常有用。本书中的很多图像都是这样的创建的。
imsave() 函数可以从 scipy.misc 模块中载入。要将数组
im 保存到文件中,可以使用下面的命令:
from scipy.misc import imsave
imsave('test.jpg',im) |
scipy.misc 模块同样包含了著名的 Lena 测试图像:
该脚本返回一个 512×512 的灰度图像数组。
4所有 Pylab 图均可保存为多种图像格式,方法是点击图像窗口中的“保存”按钮。
1.5 高级示例:图像去噪
我们通过一个非常实用的例子——图像的去噪——来结束本章。图像去噪是在去除图像噪声的同时,尽可能地保留图像细节和结构的处理技术。我们这里使用
ROF(Rudin-Osher-Fatemi)去噪模型。该模型最早出现在文献 [28] 中。图像去噪对于很多应用来说都非常重要;这些应用范围很广,小到让你的假期照片看起来更漂亮,大到提高卫星图像的质量。ROF
模型具有很好的性质:使处理后的图像更平滑,同时保持图像边缘和结构信息。
ROF 模型的数学基础和处理技巧非常高深,不在本书讲述范围之内。在讲述如何基于 Chambolle
提出的算法 [5] 实现 ROF 求解器之前,本书首先简要介绍一下 ROF 模型。
一幅(灰度)图像 I 的全变差(Total Variation,TV)定义为梯度范数之和。在连续表示的情况下,全变差表示为:
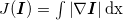 (1.1) (1.1)
在离散表示的情况下,全变差表示为:
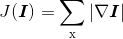
其中,上面的式子是在所有图像坐标 x=[x, y] 上取和。
在 Chambolle 提出的 ROF 模型里,目标函数为寻找降噪后的图像 U,使下式最小:
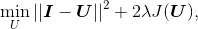
其中范数 ||I-U|| 是去噪后图像 U 和原始图像 I 差异的度量。也就是说,本质上该模型使去噪后的图像像素值“平坦”变化,但是在图像区域的边缘上,允许去噪后的图像像素值“跳跃”变化。
按照论文 [5] 中的算法,我们可以按照下面的代码实现 ROF 模型去噪:
from numpy import
*
def denoise(im,U_init,tolerance=0.1,tau=0.125,tv_weight=100):
""" 使用A. Chambolle(2005)在公式(11)中的计算步骤实现Rudin-Osher-Fatemi(ROF)去噪模型
输入:含有噪声的输入图像(灰度图像)、U 的初始值、TV 正则项权值、步长、停业条件
输出:去噪和去除纹理后的图像、纹理残留"""
m,n = im.shape # 噪声图像的大小
# 初始化
U = U_init
Px = im # 对偶域的x 分量
Py = im # 对偶域的y 分量
error = 1
while (error > tolerance):
Uold = U
# 原始变量的梯度
GradUx = roll(U,-1,axis=1)-U # 变量U 梯度的x 分量
GradUy = roll(U,-1,axis=0)-U # 变量U 梯度的y 分量
# 更新对偶变量
PxNew = Px + (tau/tv_weight)*GradUx
PyNew = Py + (tau/tv_weight)*GradUy
NormNew = maximum(1,sqrt(PxNew**2+PyNew**2))
Px = PxNew/NormNew # 更新x 分量(对偶)
Py = PyNew/NormNew # 更新y 分量(对偶)
# 更新原始变量
RxPx = roll(Px,1,axis=1) # 对x 分量进行向右x 轴平移
RyPy = roll(Py,1,axis=0) # 对y 分量进行向右y 轴平移
DivP = (Px-RxPx)+(Py-RyPy) # 对偶域的散度
U = im + tv_weight*DivP # 更新原始变量
# 更新误差
error = linalg.norm(U-Uold)/sqrt(n*m);
return U, |
|
