| 编辑推荐: |
文章介绍了CNN基本结构,卷积神经网络,以及CNN前向传播算法全过程等,希望对您能有所帮助。
本文来自于csdn,由火龙果软件Luca编辑、推荐。 |
|
1.CNN基本结构

首先我们来看看卷积神经网络(CNN)的基本结构。如上图所示,可以看出最左边的图片就是我们的输入层,计算机理解为输入若干个矩阵。接着是卷积层(Convolution
Layer),卷积层是CNN所特有的,卷积层使用的激活函数是ReLU,之前在DNN之中介绍过ReLU的激活函数,形式如ReLU=max(0,x)
。卷积层后面的是池化层,池化层也是CNN所特有的,池化层没有激活函数。
卷积层+池化层的组合可以在CNN隐藏层中出现多次,实际使用中根据模型需要而定。同时我们也可以灵活使用卷积层+卷积层,或者卷积层+卷积层+池化层的组合,卷积层+池化层的组合在构建模型时没有限制,但最常见的CNN都是若干卷积层+池化层的组合。
在若干卷积层+池化层的组合后面是全连接层(Fully Connected Layer),全连接层就是之前讲到的DNN结构,只是输出层使用了Softmax激活函数来做图像识别的分类。从上面模型可以看出,CNN相对于DNN,比较特殊的是卷积层和池化层。如果之前熟悉DNN的话,只要把卷积层和池化层的原理理解清楚,那么CNN就简单啦。
2.卷积
既然是学习卷积神经网络,那自然需要了解什么是卷积。在学习高等数学的时候,微积分中卷积表达式和其离散形式如下所示。

当然也可以用矩阵进行表达,其中*****表示卷积。
s(t)=(X*W)(t)
如果是二维的卷积,则其表达式如下所示。

在CNN中,虽然我们也是说卷积,但严格意义上和数学上所定义的卷积稍有不同,比如对于二维的卷积,其定义如下所示,其中X为输入,W为卷积核。如果X是二维输入,那么W也是二维矩阵,如果X是多维张量,那么W也是多维张量。

卷积有什么简单利用呢?我们举个例子,假如有两枚骰子,然后把骰子扔出去,求两枚骰子点数之和加起来为4的概率是多少。
上述例子的关键点便是两个骰子点数之和加起来要等于4,这正是卷积的应用场景。假设利用f表示第一枚骰子,g表示第二枚骰子。f(1)表示点数为1的概率,f(2)表示点数为2的概率。那么两枚骰子点数加起来为4的情况有f(1)g(3)、f(2)g(2)、f(3)g(1),因此两枚骰子点数加起来为4的概率为f(1)g(3)+f(2)g(2)+f(3)g(1)。符合卷积的定义,那么转换成卷积的标准形式便是

3.CNN卷积层
现在我们来深入CNN中的卷积层,如下图所示,针对图像进行卷积计算。图中的输入是二维的3*4的矩阵,卷积核是2*2的矩阵。这里我们假设卷积是每次移动一个像素来进行卷积,首先对左上角2*2局部和卷积核进行卷积计算,即各个位置的元素相乘再相加,得到的输出值S00为aw+bx+ey+fz。接着我们将输入的局部向右平移一个像素,现在是(b,c,f,g)四个元素构成的矩阵和卷积核进行卷积,这样便能够得到值为S01的元素。同样的方法能够得到S02,S10,S11,S12的元素,最后能够得到为2*3的输出矩阵S。

下面我们再看一个动态的卷积过程,其中输入是5*5的矩阵,卷积核是3*3的矩阵,卷积的步幅是一个像素,卷积的结果是3*3的矩阵。



上面举例都是二维的输入,卷积过程比较简单,那么如果输入是多维怎么计算呢?比如输入对应的是彩色图像,每个矩阵分别对应R、G、B矩阵。在斯坦福大学cs231n课程上,有个动态例子,链接为http://cs231n.github.io/assets/conv-demo/index.html,可以看着动图理解。
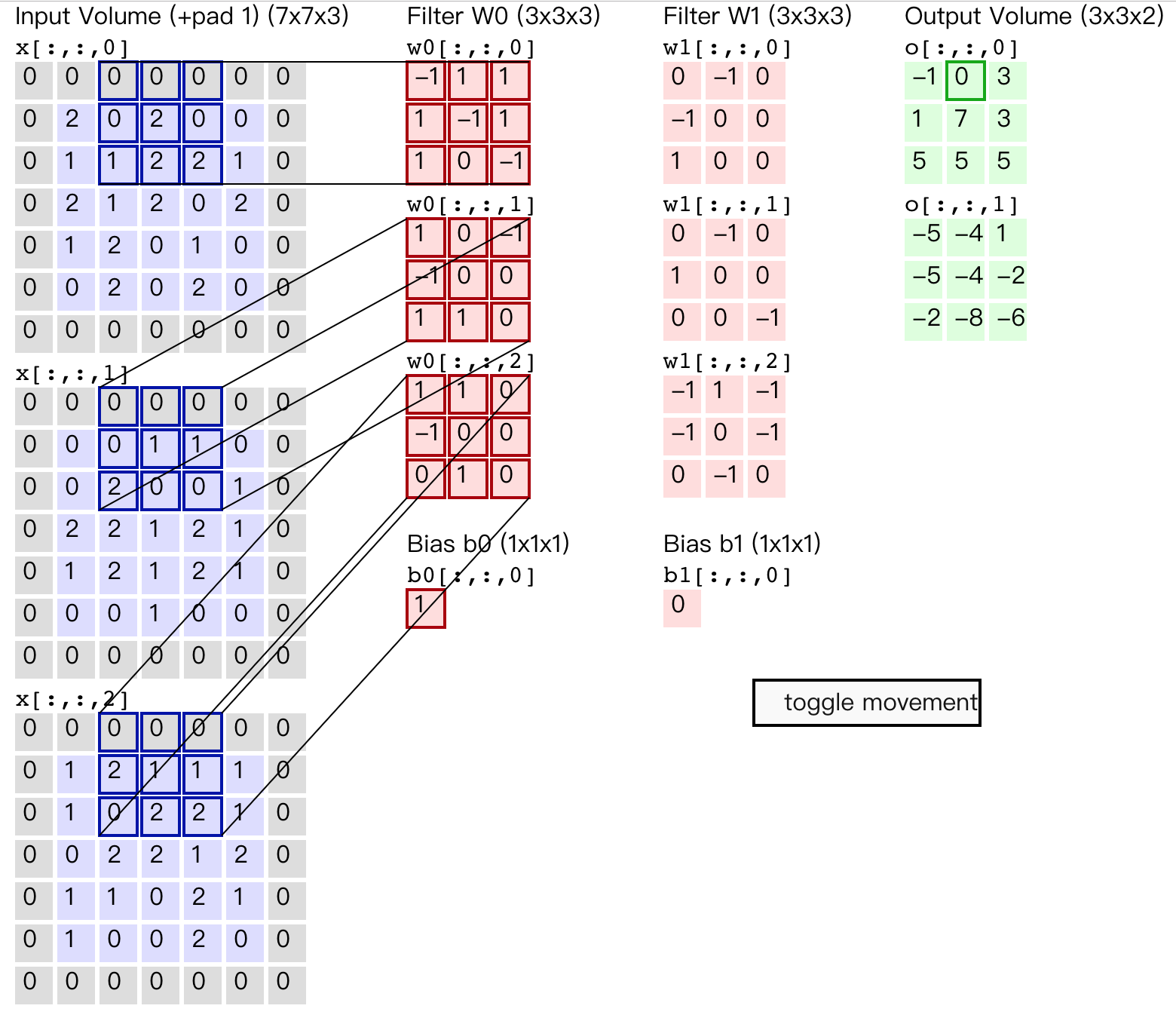
其中原输入矩阵为3个5*5的矩阵,在输入周围加上了1的padding,变成了3个7*7的矩阵。另外使用了两个卷积核,我们只关注于卷积核W0。由于输入是3个7*7的矩阵,或者说是7*7*3的张量,那么对应的卷积核W0应该是3*3*3的张量。另外这里每次卷积计算移动2个像素,也就是步幅为2。
最终的卷积过程和上面的2维矩阵计算类似,这里采用的是两个张量的三个子矩阵计算后,再把卷积的结果相加,最后再加上偏移量b。因此7*7*3的张量和3*3*3的卷积核张量W0计算后,结果是一个3*3的矩阵,同时由于我们有两个卷积核,那么最终结果便是3*3*2的张量。如果把上面的卷积过程用数学表达出来的话,那么表达式如下所示,其中n_in为输入矩阵的个数,或者说是最后一维的维数。Xk代表第k个输入矩阵,Wk代表第k个子卷积核矩阵,s(i,j)即卷积核W对应的输出矩阵元素的值。

4.CNN池化层
CNN池化层就是对输入张量的各个子矩阵进行压缩,假如是2*2的池化,那么就是将子矩阵的每2*2的元素变成一个元素,如果是3*3的池化,便是将子矩阵每3*3的元素变成一个元素,这样输入矩阵的维度也就降低。常见的池化标准是Max或者Average,即取对应区域的最大值或者平均值。如下图所示,4*4的矩阵在池化后变成2*2的矩阵,矩阵维度进行了压缩。

5.CNN前向传播
前面已经了解卷积神经网络的基本结构,包括输入层、若干卷积层+ReLU激活函数、若干的池化层、DNN全连接层,以及最后用Softmax激活函数的输出层。以彩色的汽车样本图像为例,图中的CONV即为卷积层、POLL即为池化层,FC即为DNN的全连接层。要理解CNN的前向传播算法,重点是输入层的前向传播、卷积层的前向传播、池化层的前向传播。另外全连接层传播和用Softmax激活函数的输出层的前向传播已经在DNN中讲解,这里不再赘述。

6.CNN输入层前向传播到卷积层
以图像为例,如果样本是二维的黑白图片,那么输入层X便是一个矩阵,矩阵的值等于图片的各个像素的值,这时和卷积层相连的卷积核W也就是一个矩阵。如果样本是RGB彩色图片,那么输入X便是3个矩阵,即每个对应R、G、B的矩阵,或者说是一个张量,这时和卷积层相连的卷积核W也是张量,每个卷积核都由3个子矩阵组成。同样的方法,对于3D的彩色图片,输入X可以是4维、5维等的张量,那么对应的卷积核W也是个高维的张量。不管维度多少,对于我们的输入,前向传播算法可以表示为如下所示,其中上标表示层数,*****表示卷积,b表示偏倚,σ表示激活函数,一般都是ReLU激活函数。

和DNN的前向传播比较一下,两者形式非常像,只是CNN这儿是张量的卷积,而不是矩阵的乘法。最后,我们需要定义一些CNN模型参数,即为
卷积核个数K。假设我们有K个卷积核,那么我们输入层的输出就有K个,即第二层卷积层的输入有K个。
卷积核中每个子矩阵的大小。一般我们都用子矩阵为方振的卷积核,比如F*F的子矩阵。
填充Padding(简称P)。卷积的时候,为了可以更好的识别边缘,一般会在输入矩阵周围加上若干圈的0再进行卷积,加多少圈则P为多少。
步幅Stride(简称S)。即在卷积过程中每次移动的像素距离大小。
7.隐藏层前向传播到卷积层
假设隐藏层的输出是M个矩阵对应的三维张量,则输出到卷积层的卷积核也是M个子矩阵对应的三维张量,这时表达式如下所示。其中上标代表层数,*****表示卷积,b表示偏倚量,σ表示激活函数,这里一般用ReLU。

以可以写成M个子矩阵卷积后对应位置想加的形式,即为

这里和上节的区别在于,这里的输入是隐藏层来的,而不是我们输入原始图片所形成的矩阵。同样,这里我们也需要定义卷积核的个数K,卷积核子矩阵的维度F,填充大小P以及步幅S。
8.隐藏层前向传播到池化层
池化层的处理逻辑比较简单,目的便是对输入矩阵进行缩小概括。比如输入的矩阵是N*N维的,而需要的池化大小区域是k*k维的,那么输出的矩阵都是(N/k)*(N/k)维度。这里需要定义的CNN模型参数为
池化区域的大小k。
池化的标准,一般是Max或者Average。
9.隐藏层前向传播到全连接层
由于全连接层就是普通的DNN模型结构,因此我们可以直接使用DNN的前向传播算法逻辑,表达式如下所示,这里的激活函数一般用sigmoid或者tanh函数。

经过若干全连接层之后,最后一层为Softmax输出层。此时输出层和普通的全连接层唯一的区别是,激活函数是Softmax函数。这里需要定义的CNN模型参数为
全连接层的激活函数。
全连接层各层神经元的个数。
10.CNN前向传播算法总结
输入:1个图片样本,CNN模型的层数L和所有隐藏层的类型。对于卷积层,要定义卷积核的大小K,卷积核子矩阵的维度F,填充大小P,步幅S。对于池化层,要定义池化层区域大小k和池化标准(Max或Average)。对于全连接层,定义全连接层的激活函数(输出层除外)和各层神经元的个数。
输出:CNN模型的输出aL aL。
根据输入层的填充大小P,填充原始图片的边缘,得到输入张量a1。
初始化所有隐藏层的参数W,b。
from 2 to L-1
如果l ll层是卷积层,其中*****表示卷积,则输出为

如果第l ll层是池化层,则输出为al=pool(al-1),这里的pool指按照池化区域大小k和池化标准将输入张量缩小的过程。
如果第l ll层是全连接层,则输出为

对于输出层第L层

上面就是CNN前向传播算法全过程。 |
