| 编辑推荐: |
本文主要介绍了什么是直方图?通过直方图你可以对整幅图像的灰度分布有一个整体的了解,
希望对您的学习有所帮助。
本文来自于博客园,由火龙果软件Alice编辑、推荐。 |
|
22 直方图
22.1 直方图的计算,绘制与分析
目标
使用 OpenCV 或 Numpy 函数计算直方图
使用 Opencv 或者 Matplotlib 函数绘制直方图
将要学习的函数有:cv2.calcHist(),np.histogram()
原理
什么是直方图呢?通过直方图你可以对整幅图像的灰度分布有一个整体的了解。直方图的
x 轴是灰度值(0 到 255),y 轴是图片中具有同一个灰度值的点的数目。
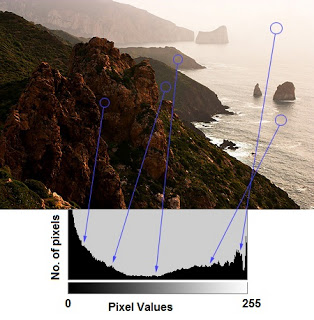
直方图其实就是对图像的另一种解释。一下图为例,通过直方图我们可以对图像的对比度,亮度,灰度分布等有一个直观的认识。几乎所有的图像处理软件都提供了直方图分析功能。下图来自Cambridge
in Color website,强烈推荐你到这个网站了解更多知识。
让我们来一起看看这幅图片和它的直方图吧。(要记住,直方图是根据灰度图像绘制的,而不是彩色图像)。直方图的左边区域像是了暗一点的像素数量,右侧显示了亮一点的像素的数量。从这幅图上你可以看到灰暗的区域比两的区域要大,而处于中间部分的像素点很少。
22.1.1 统计直方图
现在我们知道什么是直方图了,那怎样获得一副图像的直方图呢?
OpenCV 和 Numpy 都有内置函数做这件事。在使用这些函数之前我们有必要想了解一下直方图相关的术语。
BINS:上面的直方图显示了每个灰度值对应的像素数。如果像素值为 0到
255,你就需要 256 个数来显示上面的直方图。但是,如果你不需要知道每一个像素值的像素点数目的,而只希望知道两个像素值之间的像素点数目怎么办呢?举例来说,我们想知道像素值在
0 到 15 之间的像素点的数目,接着是 16 到 31,....,240 到 255。我们只需要
16 个值来绘制直方图。OpenCVTutorials on histograms中例子所演示的内容。
那到底怎么做呢?你只需要把原来的 256 个值等分成 16 小组,取每组的总和。而这里的每一个小组就被成为
BIN。第一个例子中有 256 个 BIN,第二个例子中有 16 个 BIN。在 OpenCV 的文档中用
histSize 表示 BINS。
DIMS:表示我们收集数据的参数数目。在本例中,我们对收集到的数据只考虑一件事:灰度值。所以这里就是
1。
RANGE:就是要统计的灰度值范围,一般来说为 [0,256],也就是说所有的灰度值
使用 OpenCV 统计直方图 函数 cv2.calcHist 可以帮助我们统计一幅图像的直方图
可以帮助我们统计一幅图像的直方图。我们一起来熟悉一下这个函数和它的参数:
cv2.calcHist(images,channels,mask,
histSize,ranges[,hist[,accumulate]]) |
1. images: 原图像(图像格式为 uint8 或 float32)。当传入函数时应该用中括号
[] 括起来,例如:[img]。
2. channels: 同样需要用中括号括起来,它会告诉函数我们要统计那幅图像的直方图。如果输入图像是灰度图,它的值就是
[0];如果是彩色图像的话,传入的参数可以是 [0],[1],[2] 它们分别对应着通道 B,G,R。
3. mask: 掩模图像。要统计整幅图像的直方图就把它设为 None。但是如果你想统计图像某一部分的直方图的话,你就需要制作一个掩模图像,并使用它。(后边有例子)
4. histSize:BIN 的数目。也应该用中括号括起来,例如:[256]。
5. ranges: 像素值范围,通常为 [0,256]
让我们从一副简单图像开始吧。以灰度格式加载一幅图像并统计图像的直方图。
img = cv2.imread('home.jpg',0)
# 别忘了中括号 [img],[0],None,[256],[0,256] ,只有 mask
没有中括号
hist = cv2.calcHist([img],[0],None,[256],[0,256]) |
hist 是一个 256x1 的数组,每一个值代表了与次灰度值对应的像素点数目。
使用 Numpy 统计直方图 Numpy 中的函数 np.histogram() 也可以帮我们统计直方图。你也可以尝试一下下面的代码:
#img.ravel() 将图像转成一维数组,这里没有中括号。
hist,bins = np.histogram(img.ravel(),256,[0,256])
hist 与上面计算的一样。但是这里的 bins 是 257,因为 Numpy 计算
bins 的方式为:0-0.99,1-1.99,2-2.99 等。所以最后一个范围是 255-255.99。
为了表示它,所以在 bins 的结尾加上了 256。但是我们不需要 256,到 255就够了。
其 他:Numpy 还 有 一 个 函 数 np.bincount(), 它 的 运 行 速 度 是np.histgram
的 十 倍。 所 以 对 于 一 维 直 方 图, 我 们 最 好 使 用 这 个函 数。 使 用
np.bincount 时 别 忘 了 设 置 minlength=256。 例 如,
hist=np.bincount(img.ravel() ,minlength=256)
注意:OpenCV 的函数要比 np.histgram() 快 40 倍。所以坚持使用OpenCV
函数。
现在是时候学习绘制直方图了。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('home.jpg',0)
plt.hist(img.ravel(),256,[0,256]); plt.show() |
22.1.2 绘制直方图
有两种方法来绘制直方图:
1. Short Way(简单方法):使用 Matplotlib
中的绘图函数。
2. Long Way(复杂方法):使用 OpenCV 绘图函数
使用 Matplotlib Matplotlib 中有直方图绘制函数:matplotlib.pyplot.hist()
它可以直接统计并绘制直方图。你应该使用函数 calcHist() 或 np.histogram()
统计直方图。
你会得到下面这样一幅图:
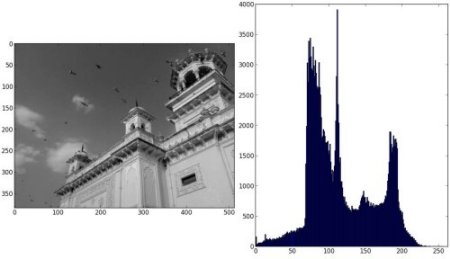
或者你可以只使用 matplotlib 的绘图功能,这在同时绘制多通道(BGR)的直方图,很有用。但是你首先要告诉绘图函数你的直方图数据在哪里。运行一下下面的代码:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('home.jpg')
color = ('b','g','r')
# 对一个列表或数组既要遍历索引又要遍历元素时
# 使用内置 enumerrate 函数会有更加直接,优美的做法
#enumerate 会将数组或列表组成一个索引序列。
# 使我们再获取索引和索引内容的时候更加方便
for i,col in enumerate(color):
histr = cv2.calcHist([img],[i],None,[256],[0,256])
plt.plot(histr,color = col)
plt.xlim([0,256])
plt.show() |
结果:
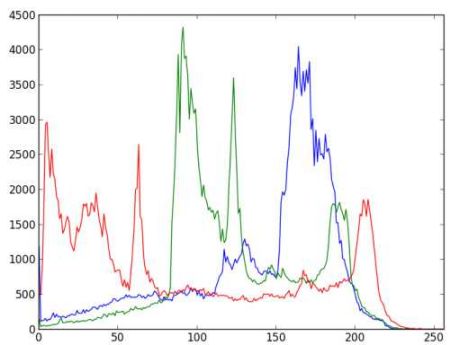
从上边的直方图你可以推断出蓝色曲线靠右侧的最多(很明显这些就是天空)
使用 OpenCV 使用 OpenCV 自带函数绘制直方图比较麻烦,这里不作介绍,有兴趣可以自己研究。可以参考
OpenCV-Python2 的官方示例。
22.1.3 使用掩模
要统计图像某个局部区域的直方图只需要构建一副掩模图像。将要统计的部分设置成白色,其余部分为黑色,就构成了一副掩模图像。然后把这个掩模图像传给函数就可以了。
img = cv2.imread('home.jpg',0)
# create a mask
mask = np.zeros(img.shape[:2], np.uint8)
mask[100:300, 100:400] = 255
masked_img = cv2.bitwise_and(img,img,mask =
mask)
# Calculate histogram with mask and without
mask
# Check third argument for mask
hist_full = cv2.calcHist([img],[0],None,[256],[0,256])
hist_mask = cv2.calcHist([img],[0],mask,[256],[0,256])
plt.subplot(221), plt.imshow(img, 'gray')
plt.subplot(222), plt.imshow(mask,'gray')
plt.subplot(223), plt.imshow(masked_img, 'gray')
plt.subplot(224), plt.plot(hist_full), plt.plot(hist_mask)
plt.xlim([0,256])
plt.show() |
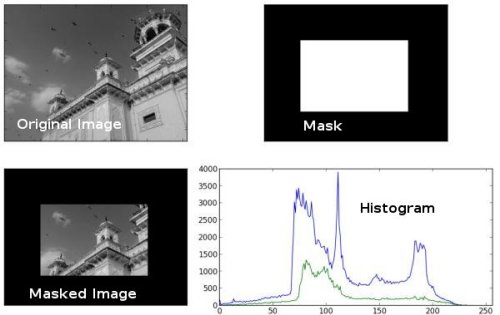
结果如下,其中蓝线是整幅图像的直方图,绿线是进行掩模之后的直方图。
22.2 直方图均衡化
目标
本小节我们要学习直方图均衡化的概念,以及如何使用它来改善图片的对比。
原理
想象一下如果一副图像中的大多是像素点的像素值都集中在一个像素值范围之内会怎样呢?例如,如果一幅图片整体很亮,那所有的像素值应该都会很高。但是一副高质量的图像的像素值分布应该很广泛。所以你应该把它的直方图做一个横向拉伸(如下图),这就是直方图均衡化要做的事情。通常情况下这种操作会改善图像的对比度。

推荐你去读读维基百科中关于直方图均衡化的条目。其中的解释非常给力,读完之后相信你就会对整个过程有一个详细的了解了。我们先看看怎样使用Numpy
来进行直方图均衡化,然后再学习使用 OpenCV 进行直方图均衡化。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('wiki.jpg',0)
#flatten() 将数组变成一维
hist,bins = np.histogram(img.flatten(),256,[0,256])
# 计算累积分布图
cdf = hist.cumsum()
cdf_normalized = cdf * hist.max()/ cdf.max()
plt.plot(cdf_normalized, color = 'b')
plt.hist(img.flatten(),256,[0,256], color = 'r')
plt.xlim([0,256])
plt.legend(('cdf','histogram'), loc = 'upper left')
plt.show() |

我们可以看出来直方图大部分在灰度值较高的部分,而且分布很集中。而我们希望直方图的分布比较分散,能够涵盖整个
x 轴。所以,我们就需要一个变换函数帮助我们把现在的直方图映射到一个广泛分布的直方图中。这就是直方图均衡化要做的事情。
我们现在要找到直方图中的最小值(除了 0),并把它用于 wiki
中的直方图均衡化公式。但是我在这里使用了 Numpy 的掩模数组。对于掩模数组的所有操作都只对 non-masked
元素有效。你可以到 Numpy 文档中获取更多掩模数组的信息。
# 构建 Numpy 掩模数组,
cdf 为原数组,当数组元素为 0 时,掩盖(计算时被忽略)。
cdf_m = np.ma.masked_equal(cdf,0)
cdf_m = (cdf_m - cdf_m.min())*255/(cdf_m.max()-cdf_m.min())
# 对被掩盖的元素赋值,这里赋值为 0
cdf = np.ma.filled(cdf_m,0).astype('uint8') |
现在就获得了一个表,我们可以通过查表得知与输入像素对应的输出像素的值。我们只需要把这种变换应用到图像上就可以了。
我们再根据前面的方法绘制直方图和累积分布图,结果如下:
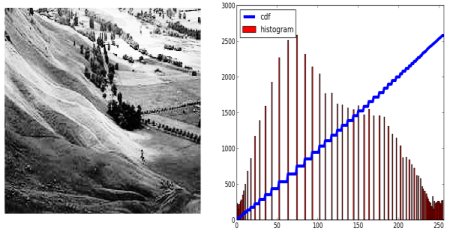
另一个重要的特点是,即使我们的输入图片是一个比较暗的图片(不像上边我们用到到的整体都很亮的图片),在经过直方图均衡化之后也能得到相同的结果。因此,直方图均衡化经常用来使所有的图片具有相同的亮度条件的参考工具。这在很多情况下都很有用。例如,脸部识别,在训练分类器前,训练集的所有图片都要先进行直方图均衡化从而使它们达到相同的亮度条件。
22.2.1 OpenCV 中的直方图均衡化
OpenCV 中的直方图均衡化函数为 cv2.equalizeHist()。这个函数的输入图片仅仅是一副灰度图像,输出结果是直方图均衡化之后的图像。
下边的代码还是对上边的那幅图像进行直方图均衡化:
img = cv2.imread('wiki.jpg',0)
equ = cv2.equalizeHist(img)
res = np.hstack((img,equ)) #stacking images side-by-side
cv2.imwrite('res.png',res) |

现在你可以拿一些不同亮度的照片自己来试一下了。当直方图中的数据集中在某一个灰度值范围内时,直方图均衡化很有用。但是如果像素的变化很大,而且占据的灰度范围非常广时,例如:既有很亮的像素点又有很暗的像素点时。请查看更多资源中的
SOF 链接。
22.2.2 CLAHE
有限对比适应性直方图均衡化我们在上边做的直方图均衡化会改变整个图像的对比度,但是在很多情况下,这样做的效果并不好。例如,下图分别是输入图像和进行直方图均衡化之后的输出图像。

的确在进行完直方图均衡化之后,图片背景的对比度被改变了。但是你再对比一下两幅图像中雕像的面图,由于太亮我们丢失了很多信息。造成这种结果的根本原因在于这幅图像的直方图并不是集中在某一个区域(试着画出它的直方图,你就明白了)。
为了解决这个问题,我们需要使用自适应的直方图均衡化。这种情况下,整幅图像会被分成很多小块,这些小块被称为“tiles”(在
OpenCV 中 tiles 的大小默认是 8x8),然后再对每一个小块分别进行直方图均衡化(跟前面类似)。
所以在每一个的区域中,直方图会集中在某一个小的区域中(除非有噪声干扰)。如果有噪声的话,噪声会被放大。为了避免这种情况的出现要使用对比度限制。对于每个小块来说,如果直方图中的
bin 超过对比度的上限的话,就把其中的像素点均匀分散到其他 bins 中,然后在进行直方图均衡化。最后,为了去除每一个小块之间“人造的”(由于算法造成)边界,再使用双线性差值,对小块进行缝合。
下面的代码显示了如何使用 OpenCV 中的 CLAHE。
import numpy
as np
import cv2
img = cv2.imread('tsukuba_l.png',0)
# create a CLAHE object (Arguments are optional).
# 不知道为什么我没好到 createCLAHE 这个模块
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)
cv2.imwrite('clahe_2.jpg',cl1) |
下面就是结果了,与前面的结果对比一下,尤其是雕像区域:

22.3 2D 直方图
目标
本节我们会学习如何绘制 2D 直方图,我们会在下一节中使用到它。
22.3.1 介绍
在前面的部分我们介绍了如何绘制一维直方图,之所以称为一维,是因为我们只考虑了图像的一个特征:灰度值。但是在
2D 直方图中我们就要考虑两个图像特征。对于彩色图像的直方图通常情况下我们需要考虑每个的颜色(Hue)和饱和度(Saturation)。根据这两个特征绘制
2D 直方图。
OpenCV 的官方文档中包含一个创建彩色直方图的例子。本节就是要和大家一起来学习如何绘制颜色直方图,这会对我们下一节学习直方图投影有所帮助。
22.3.2 OpenCV 中的 2D 直方图
使用函数 cv2.calcHist() 来计算直方图既简单又方便。如果要绘制颜色直方图的话,我们首先需要将图像的颜色空间从
BGR 转换到 HSV。(记住,计算一维直方图,要从 BGR 转换到 HSV)。计算 2D 直方图,函数的参数要做如下修改:
channels=[0 ,1] 因为我们需要同时处理 H 和 S
两个通道。
bins=[180 ,256]H 通道为 180,S 通道为 256。
range=[0 ,180 ,0 ,256]H 的取值范围在 0
到 180,S 的取值范围在 0 到 256。
代码如下:
import cv2
import numpy as np
img = cv2.imread('home.jpg')
hsv = cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
hist = cv2.calcHist([hsv], [0, 1], None, [180,
256], [0, 180, 0, 256]) |
这就搞定了,简单吧!
22.3.3 Numpy 中 中 2D 直方图
Numpy 同样提供了绘制 2D 直方图的函数:np.histogram2d()。(还记得吗,绘制
1D 直方图时我们使用的是 np.histogram())。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('home.jpg')
hsv = cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
hist, xbins, ybins = np.histogram2d(h.ravel(),
s.ravel(),[180,256],[[0,180],[0,256]]) |
第一个参数是 H 通道,第二个参数是 S 通道,第三个参数是 bins 的数目,第四个参数是数值范围。
现在我们要看看如何绘制颜色直方图。
22.3.4 绘制 2D 直方图
方法 1 :使用 cv2.imshow() 我们得到结果是一个 180x256
的两维数组。所以我们可以使用函数 cv2.imshow() 来显示它。但是这是一个灰度图,除非我们知道不同颜色
H 通道的值,否则我们根本就不知道那到底代表什么颜色。
方法 2 :使用 Matplotlib() 我们还可以使用函数 matplotlib.pyplot.imshow()来绘制
2D 直方图,再搭配上不同的颜色图(color_map)。这样我们会对每个点所代表的数值大小有一个更直观的认识。但是跟前面的问题一样,你还是不知道那个数代表的颜色到底是什么。虽然如此,我还是更喜欢这个方法,它既简单又好用。
注意:在使用这个函数时,要记住设置插值参数为 nearest。
代码如下:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('home.jpg')
hsv = cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
hist = cv2.calcHist( [hsv], [0, 1], None, [180,
256], [0, 180, 0, 256] )
plt.imshow(hist,interpolation = 'nearest')
plt.show() |
下面是输入图像和颜色直方图。X 轴显示 S 值,Y 轴显示 H 值。
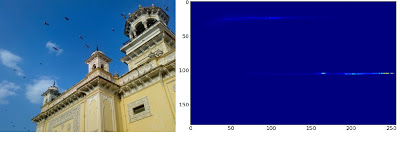
在直方图中,你可以看到在 H=100,S=100 附近有比较高的值。这部分与天的蓝色相对应。同样另一个峰值在
H=25 和 S=100 附近。这一宫殿的黄色相对应。你可用通过使用图像编辑软件(GIMP)修改图像,然后在绘制直方图看看我说的对不对。
方法 3 :OpenCV ?格 在官方文档中有一个关于颜色直方图的例子。运行一下这个代码,你看到的颜色直方图也显示了对应的颜色。简单来说就是:输出结果是一副由颜色编码的直方图。效果非常好(虽然要添加很多代码)。
在那个代码中,作者首先创建了一个 HSV 格式的颜色地图,然后把它转换成 BGR 格式。再将得到的直方图与颜色直方图相乘。作者还用了几步来去除小的孤立的的点,从而得到了一个好的直方图。
我把对代码的分析留给你们了,自己去玩一下把。下边是对上边的图运行这段代码之后得到的结果:
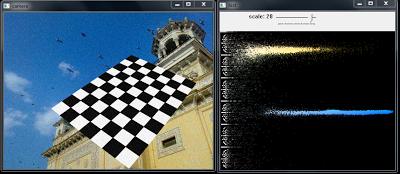
从直方图中我们可以很清楚的看出它们代表的颜色,蓝色,换色,还有棋盘带来的白色,漂亮!!!
# -*- coding:
utf-8 -*-
#!/usr/bin/env python
import numpy as np
import cv2
from time import clock
import sys
import video
#video 模块也是 opencv 官方文档中自带的
if __name__ == '__main__':
# 构建 HSV 颜色地图
hsv_map = np.zeros((180, 256, 3), np.uint8)
# np.indices 可以返回由数组索引构建的新数组。
# 例如: np.indices (( 3,2 ));其中( 3,2 )
为原来数组的维度:行和列。
# 返回值首先看输入的参数有几维:( 3,2 )有 2 维,
所以从输出的结果应该是
# [[a],[b]], 其中包含两个 3 行, 2 列数组。
# 第二看每一维的大小,第一维为 3, 所以 a 中的值就
0 到 2 (最大索引数),
# a 中的每一个值就是它的行索引;同样的方法得到 b
(列索引)
# 结果就是
# array([[[0, 0],
# [1, 1],
# [2, 2]],
#
# [[0, 1],
# [0, 1],
# [0, 1]]])
h, s = np.indices(hsv_map.shape[:2])
hsv_map[:,:,0] = h
hsv_map[:,:,1] = s
hsv_map[:,:,2] = 255
hsv_map = cv2.cvtColor(hsv_map, cv2.COLOR_HSV2BGR)
cv2.imshow('hsv_map', hsv_map)
cv2.namedWindow('hist', 0)
hist_scale = 10
def set_scale(val):
global hist_scale
hist_scale = val
cv2.createTrackbar('scale', 'hist', hist_scale,
32, set_scale)
try: fn = sys.argv[1]
except: fn = 0
cam = video.create_capture(fn, fallback='synth:bg=../cpp/baboon.jpg:
class=chess:noise=0.05')
while True:
flag, frame = cam.read()
cv2.imshow('camera', frame)
# 图像金字塔
# 通过图像金字塔降低分辨率,但不会对直方图有太大影响。
# 但这种低分辨率,可以很好抑制噪声,
从而去除孤立的小点对直方图的影响。
small = cv2.pyrDown(frame)
hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
# 取 v 通道 ( 亮度 ) 的值。
# 没有用过这种写法,还是改用最常见的用法。
#dark = hsv[...,2] < 32
# 此步操作得到的是一个布尔矩阵,小于 32 的为真,
大于 32 的为假。
dark = hsv[:,:,2] < 32
hsv[dark] = 0
h = cv2.calcHist( [hsv], [0, 1], None, [180, 256],
[0, 180, 0, 256] )
#numpy.clip(a, a_min, a_max, out=None)[source]
#Given an interval, values outside the interval
are clipped to the interval edges.
#For example, if an interval of [0, 1] is specified,
values smaller
#than 0 become 0, and values larger than 1 become
1.
#>>> a = np.arange(10)
#>>> np.clip(a, 1, 8)
#array([1, 1, 2, 3, 4, 5, 6, 7, 8, 8])
h = np.clip(h*0.005*hist_scale, 0, 1)
#In numpy one can use the 'newaxis' object
in
the slicing syntax to create an
#axis of length one. one can also use None
instead
of newaxis,
#the effect is exactly the same
#h 从一维变成 3 维
vis = hsv_map*h[:,:,np.newaxis] / 255.0
cv2.imshow('hist', vis)
ch = 0xFF & cv2.waitKey(1)
if ch == 27:
break
cv2.destroyAllWindows() |
22.4 直方图反向投影
目标
本节我们将要学习直方图反向投影
原理
直方图反向投影是由 Michael J. Swain 和 Dana
H. Ballard 在他们的文章“Indexing via color histograms”中提出。
那它到底是什么呢?它可以用来做图像分割,或者在图像中找寻我们感兴趣的部分。简单来说,它会输出与输入图像(待搜索)同样大小的图像,其中的每一个像素值代表了输入图像上对应点属于目标对象的概率。用更简单的话来解释,输出图像中像素值越高(越白)的点就越可能代表我们要搜索的目标(在输入图像所在的位置)。这是一个直观的解释。直方图投影经常与
camshift算法等一起使用。
我们应该怎样来实现这个算法呢?首先我们要为一张包含我们要查找目标的图像创建直方图(在我们的示例中,我们要查找的是草地,其他的都不要)。
我们要查找的对象要尽量占满这张图像(换句话说,这张图像上最好是有且仅有我们要查找的对象)。最好使用颜色直方图,因为一个物体的颜色要比它的灰度能更好的被用来进行图像分割与对象识别。接着我们再把这个颜色直方图投影到输入图像中寻找我们的目标,也就是找到输入图像中的每一个像素点的像素值在直方图中对应的概率,这样我们就得到一个概率图像,最后设置适当的阈值对概率图像进行二值化,就这么简单。
22.4.1 Numpy 中的算法
此处的算法与上边介绍的算法稍有不同。
首先,我们要创建两幅颜色直方图,目标图像的直方图('M'),(待搜索)输入图像的直方图('I')。
import cv2
import numpy as np
from matplotlib import pyplot as plt
#roi is the object or region of object we need
to find
roi = cv2.imread('rose_red.png')
hsv = cv2.cvtColor(roi,cv2.COLOR_BGR2HSV)
#target is the image we search in
target = cv2.imread('rose.png')
hsvt = cv2.cvtColor(target,cv2.COLOR_BGR2HSV)
# Find the histograms using calcHist. Can be
done with np.histogram2d also
M = cv2.calcHist([hsv],[0, 1], None, [180, 256],
[0, 180, 0, 256] )
I = cv2.calcHist([hsvt],[0, 1], None, [180,
256], [0, 180, 0, 256] ) |
计算比值: R = \frac{M}{I} 。反向投影 R,也就是根据 R 这个”调色板“创建一副新的图像,其中的每一个像素代表这个点就是目标的概率。例如
B (x,y) =R[h(x,y),s(x,y)],其中 h 为点(x,y)处的 hue 值,s 为点(x,y)处的
saturation 值。最后加入再一个条件 B(x,y) = min[B(x,y), 1].
h,s,v = cv2.split(hsvt)
B = R[h.ravel(),s.ravel()]
B = np.minimum(B,1)
B = B.reshape(hsvt.shape[:2]) |
现在使用一个圆盘算子做卷积,B = D × B,其中 D 为卷积核。
disc = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(5,5))
B=cv2.filter2D(B,-1,disc)
B = np.uint8(B)
cv2.normalize(B,B,0,255,cv2.NORM_MINMAX) |
现在输出图像中灰度值最大的地方就是我们要查找的目标的位置了。如果我们要找的是一个区域,我们就可以使用一个阈值对图像进行二值化,这样就可以得到一个很好的结果了。
| ret,thresh =
cv2.threshold(B,50,255,0) |
就是这样。
22.4.2 OpenCV 中的反向投影
OpenCV 提供的函数 cv2.calcBackProject()
可以用来做直方图反向投影。它的参数与函数 cv2.calcHist 的参数基本相同。其中的一个参数是我们要查找目标的直方图。同样再使用目标的直方图做反向投影之前我们应该先对其做归一化处理。返回的结果是一个概率图像,我们再使用一个圆盘形卷积核对其做卷操作,最后使用阈值进行二值化。下面就是代码和结果:
import cv2
import numpy as np
roi = cv2.imread('tar.jpg')
hsv = cv2.cvtColor(roi,cv2.COLOR_BGR2HSV)
target = cv2.imread('roi.jpg')
hsvt = cv2.cvtColor(target,cv2.COLOR_BGR2HSV)
# calculating object histogram
roihist = cv2.calcHist([hsv],[0, 1], None,
[180,
256], [0, 180, 0, 256] )
# normalize histogram and apply backprojection
# 归一化:原始图像,结果图像,映射到结果图像
中的最小值,最大值,归一化类型
#cv2.NORM_MINMAX 对数组的所有值进行转化,
使它们线性映射到最小值和最大值之间
# 归一化之后的直方图便于显示,归一化之后就成了
0 到 255 之间的数了。
cv2.normalize(roihist,roihist,0,255,cv2.NORM_MINMAX)
dst = cv2.calcBackProject([hsvt],[0,1],roihist,
[0,180,0,256],1)
# Now convolute with circular disc
# 此处卷积可以把分散的点连在一起
disc = cv2.getStructuringElement(cv2.
MORPH_ELLIPSE,(5,5))
dst=cv2.filter2D(dst,-1,disc)
# threshold and binary AND
ret,thresh = cv2.threshold(dst,50,255,0)
# 别忘了是三通道图像,因此这里使用 merge
变成 3 通道
thresh = cv2.merge((thresh,thresh,thresh))
# 按位操作
res = cv2.bitwise_and(target,thresh)
res = np.hstack((target,thresh,res))
cv2.imwrite('res.jpg',res)
# 显示图像
cv2.imshow('1',res)
cv2.waitKey(0) |
下面是我使用的一幅图像。我使用图中蓝色矩形中的区域作为取样对象,再根据这个样本搜索图中所有的类似区域(草地)。

|
