| 编辑推荐: |
本文重点介绍贝叶斯分类,涉及朴素贝叶斯模型、二项独立模型、多项模型、混合模型等知识。
本文来自于cnblogs.,由火龙果软件Anna编辑、推荐。 |
|
0 引言
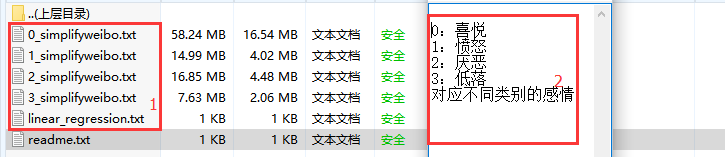
于半月前,针对文本分类进行学习,实验的目的是通过对下图1中的不同情感文本构建训练集模型,对应的下图2是对训练集的注释说明。类标0开头为喜悦类别,类标1开头的为愤怒类别,类别2开头的是厌恶类别,类别3开头的为低落类别。4个训练集文本,分别对应4个分类。如何通过训练集构造分类器,并对测试数据进行验证是本课题的最终目的。其中会涉及贝叶斯公式的理解与实现,文本的预处理(下图1中0_simplifyweibo的训练集是处理过的数据如下图),分词工具的使用,不同贝叶斯模型的构造,试验结果对比。核心思路就两点:1,模型训练阶段
2,分类预测阶段。完整流程如下:
-->训练文本预处理,构造分类器。(即对贝叶斯公式实现文本分类参数值的求解,暂时不理解没关系,下文详解)
-->构造预测分类函数
-->对测试数据预处理
-->使用分类器分类
1 四种模型结构
朴素贝叶斯模型 NaiveBayes model NM
二项独立模型 Bnary independence model BIM
多项式模型 multinomial model MM
混合模型 hyorid model HM
平滑因子混合模型 hyorid model with new smooth factore HM&NSF
2 朴素贝叶斯分类器
思想概述
-- 公式 P( Category | Document) = (P ( Document | Category
) * P( Category))/ P(Document)
-- 朴素贝叶斯分类器: P(c|d)~=P(c)*P(d|c)
-- 训练阶段:对每一个W_k,C_i估计先验条件概率P(w_k|c_i)和概率P(C_i)
-- 分类阶段:计算后验概率,返回使后验概率最大的类
-- C(d)=argmax {P(C_i)*P(d|c_i)
对于一个新的训练文档d,究竟属于如上四个类别的哪个类别?我们可以根据贝叶斯公式,只是此刻变化成具体的对象。
> P( Category | Document):测试文档属于某类的概率
> P( Category)):从文档空间中随机抽取一个文档d,它属于类别c的概率。(某类文档数目/总文档数目)
> (P ( Document | Category ):文档d对于给定类c的概率(某类下文档中单词数/某类中总的单词数)
> P(Document):从文档空间中随机抽取一个文档d的概率(对于每个类别都一样,可以忽略不计算。此时为求最大似然概率)
> C(d)=argmax {P(C_i)*P(d|c_i)}:求出近似的贝叶斯每个类别的概率,比较获取最大的概率,此时文档归为最大概率的一类,分类成功。
综上:对训练集构成训练分类器模型的过程,本质是对参数模型的求解。然后将这些参数在预测方法中使用,根据公式获取最大概率即可完成文档分类。
公式推导与解析
朴素贝叶斯公式:(假设条件:当文档d属于类c时,文档d中的元素w的取值与类c中的w的取值是独立关系[实际显示不独立,一种近似处理])
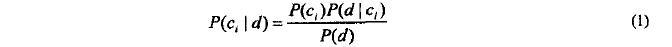
公式解析:
> P(d):从文档空间中随机抽取一个文档d的概率(对于每个类别都一样,可以忽略不计算。此时为求最大似然概率)
> P(c):从文档空间中随机抽取一个文档d,它属于类别c的概率。(某类文档数目/总文档数目)
> (P ( d| c ):文档d对于给定类c的概率(某类下文档中单词数/某类中总的单词数)
> 类别集: c={c1,c2,.....,cn}
> 文档向量: d={w1,w2,.....,wn}
> 类别集: c={c1,c2,.....,cn}
> P(c| d):测试文档d属于某类c的概率(估计条件概率)【估计概率:训练集中进行训练过程,在某种假设条件下实现的】
> MaxP(c| d):测试文档d属于某类c的最大概率
先验条件概率:
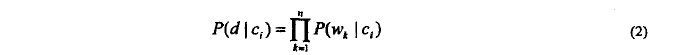
将(2)式代入(1)得:(下式中p(d)对于所有的类c都是一样的)
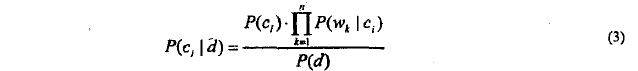
注:只要对上式中的分母求出最大值即可。分母中的左部分通过(某类文档数目/总文档数目)易得,右侧中通过求文档d和c中单词量即可。到此,解决思路和思想都有了,下面基于此完成算法。
算法介绍与实现
算法1:文本分类的朴素贝叶斯算法
训练阶段:对每一个w_k,c_i估计先验条件概率p(w_k|c_i)和概率p(c_i)。
分类阶段:计算后验概率,返回使后验概率最大的类。
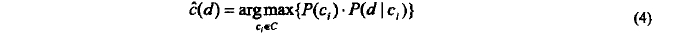
算法具体实现:
/**
* 朴素贝叶斯文本分类器
* 训练阶段
* 算法思想:文档d属于某类c的概率=文档空间随机抽取一个文档d属于某类c的概率*文档中的单词与总单词的比例
* P(c|d)~=P(c)*P(d|c)
* P(c)=classDocnum/classAlldocnum
* 计算参数:
* classDocnum:某类中的文档数目
* classAlldocnum:数据集中总的文档数目
* classWordfru:某类下文档中单词频数
* classAllwordnum:某类中总的单词数
* @param fileDirPath 训练集文件夹目录
*/ |
| package com.naivebayes.bnc;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import jeasy.analysis.MMAnalyzer;
/**
* @公式 P( Category | Document) = (P ( Document
| Category ) * P( Category))/ P(Document)
* @朴素贝叶斯分类器: P(c|d)~=P(c)*P(d|c)
* @算法思想:
* 训练阶段:对每一个W_k,C_i估计先验条件概率P(w_k|c_i)和概率P(C_i)
* 分类阶段:计算后验概率,返回使后验概率最大的类
* C(d)=argmax {P(C_i)*P(d|c_i)}
* @条件:给定目标值时属性之间相互条件独立。换言之。该假定说明给定实例的目标值情况下。观察到联合的a1,a2...an的概率正好是对每个单独属性的概率乘积:
P(a1,a2...an | Vj ) =Πi P( ai| Vj ).
* @缺点: 在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。
* @优点:决策树模型也有一些缺点,比如处理缺失数据时的困难,过度拟合问题的出现,以及忽略数据集中属性之间的相关性等,适用NBC(朴素贝叶斯分类)
* @比较:在属性相关性较小时,NBC模型的性能稍微良好。属性相关性较小的时候,其他的算法性能也很好,这是由于信息熵理论决定的。
* @author 白宁超
*
*/
public class NaiveBayesToClass {
//统计某类文档的数目
public static Map<String,Integer> classDocnum=new
HashMap<String, Integer>();
//属于类别的单词 总数
public static int classAlldocnum=0;
//统计某类中某个单词出现的次数
public static Map< String,Integer> classWordfru=new
HashMap<String, Integer>();
//统计某类中的单词总数
public static Map<String,Integer> classAllwordnum=new
HashMap<String, Integer>();
/**
* 朴素贝叶斯文本分类器
* 训练阶段
* 算法思想:文档d属于某类c的概率=文档空间随机抽取一个文档d属于某类c的概率*文档中的单词与总单词的比例
* P(c|d)~=P(c)*P(d|c)
* P(c)=classDocnum/classAlldocnum
* 计算参数:
* classDocnum:某类中的文档数目
* classAlldocnum:数据集中总的文档数目
* classWordfru:某类下文档中单词频数
* classAllwordnum:某类中总的单词数
* @param fileDirPath 训练集文件夹目录
*/
public static void BayesModel (String fileDirPath){
try{
File dir=new File(fileDirPath);
if(dir.exists() &&dir.isDirectory()){
File[] files=dir.listFiles(); //获取所有训练集文件
for(File file:files){
String classNo=file.getName().split("\\_")[0];//获取文件类标
FileInputStream stream =new FileInputStream(file);
//获取文件流
InputStreamReader strRead=new InputStreamReader(stream,"UTF-8");
//对文件进行读取,且指定编码格式
BufferedReader bufReader = new BufferedReader(strRead);
String line=null;
//读取文件内容
while((line=bufReader.readLine())!=null){
//统计某类文档的数目
if(classDocnum.containsKey(classNo)){
classDocnum.put (classNo, classDocnum.get(classNo)+1);
}
else{
classDocnum.put(classNo, 1);//第一次存数据,没有类标,但是已经读取一行,故设置1
}
String lineText = line.trim(); //除去字符串开头和末尾的空格或其他字符
String[] words = lineText.split(" ");
//遍历所有单词
for(String word:words){
//统计某类中的单词总数
if(classAllwordnum.containsKey(classNo)){
classAllwordnum.put(classNo, classAllwordnum.get(classNo)+1);
}
else{
classAllwordnum.put(classNo, 1);
}
//统计某类中某个单词出现的次数
String wordNo=classNo+"_"+word;
if(classWordfru.containsKey(wordNo)){
classWordfru.put (wordNo, classWordfru.get(wordNo)+1);
}
else{
classWordfru.put(wordNo, 1);
}
}
classAlldocnum++;
}
strRead.close();
}
}
else{
System.out.println("找不到目录文件"+fileDirPath);
}
}
catch (Exception e) {
System.out.println("出错信息描述如下:"+e.getMessage());
}
}
/**
* 对测试文本进行分类预测
* 预测阶段:
* @param testText 测试数据集
* @return 返回分类结果
*/
public static String PredictReslut (String testText){
//预测结果
String PredictResult="";
testText=SplitWords(testText, " ");//
对测试文档进行中文分词处理
String[] words=testText.split(" ");
//对字符串进行分割
double argmax = Double.NEGATIVE_INFINITY;//最大类概率(默认值为负无穷小),是否可以写成0?(无穷小本身就是接近0)
Iterator iterator= classDocnum.keySet().iterator();//遍历
while(iterator.hasNext()){
String classNo = (String) iterator.next();
double prior = classDocnum.get (classNo)/(double)classAlldocnum;//先验概率
double classcount= (double)(classAllwordnum.get(classNo)+1);//某一类的最大值
double likelihoodProbability=0; //初始化似然概率
//根据公式求解最大似然概率,其中words相当于属性即多维的
for (int i = 0; i < words.length; i++){
String word_classNo = words[i]+"_"+classNo;
//获取测试数据的单词类别
//与训练数据词库进行对比,求得相似的概率
if(classWordfru.containsKey(word_classNo)){
//将连乘装换成对数相加【ln(a*b)=lna+lnb】,提高效率
likelihoodProbability += Math.log(classWordfru.get(word_classNo)/classcount);
}
else{
likelihoodProbability += Math.log(1/classcount);
}
}
//利用自然对数e^loga = a,取得原始值
likelihoodProbability = Math.exp(likelihoodProbability)*prior;
System.out.println ("classNo:"+classNo);
System.out.println ("最大似然概率:"+argmax);
System.out.println ("似然概率:"+likelihoodProbability);
if(likelihoodProbability>argmax){
argmax = likelihoodProbability; //最大似然概率一直保持最大的似然概率
PredictResult = classNo; //返回分类的结果
}
}
System.out.println("********");
System.out.println("【朴素贝叶斯最终分类结果:】"+PredictResult);
return PredictResult;
}
/**
* 对字符串进行中文分词处理
* @param text 给定预处理的字符串
* @param splitToken 用于分割的标记。如","
* @return 处理后的字符串
*/
public static String SplitWords (String text,String
splitToken){
String result = null;
MMAnalyzer analyzer = new MMAnalyzer(); //极易中文分词
try {
result = analyzer.segment(text, splitToken);
}
catch (IOException e){
e.printStackTrace();
}
return result;
}
} |
运行结果:
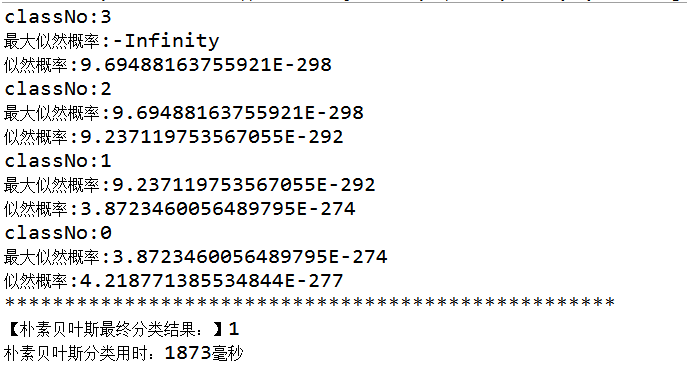
优缺点对比分析
* @条件:给定目标值时属性之间相互条件独立。换言之。该假定说明给定实例的目标值情况下。观察到联合的a1,a2...an的概率正好是对每个单独属性的概率乘积:
P(a1,a2...an | Vj ) =Πi P( ai| Vj ).
* @缺点: 在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。
* @优点:决策树模型也有一些缺点,比如处理缺失数据时的困难,过度拟合问题的出现,以及忽略数据集中属性之间的相关性等,适用NBC(朴素贝叶斯分类)
* @比较:在属性相关性较小时,NBC模型的性能稍微良好。属性相关性较小的时候,其他的算法性能也很好,这是由于信息熵理论决定的。
3 二项独立模型
思想概述
二项独立模型又称为多变量伯努利模型,是朴素贝叶斯最常用的实现模型之一。使用二值向量来表示文档,当w=1时,单词在文档中出现w=0不出现。只是在求解先验概率时候有所变化,其他和朴素贝叶斯一样。后面会涉及平滑因子避免分母为0的问题。
分类模型:对于类c_i,单词w_k的先验条件概率
二项独立模型的先验概率:(假设条件:其在一定假设条件下实现的,即给定的类c_i,文档d中单词w_k和w_i是否出现是相互独立的。)
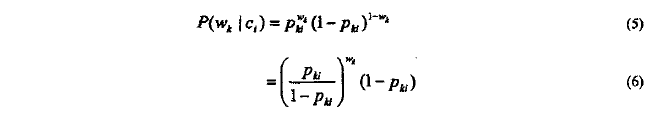
公式解析:
> 其使用二值向量来表示一个文档,即d={w1,w2,...,w|v|},其中w_k属于{0,1}
>|V|:单词表的尺寸
> w_k=1:单词w在文档中出现
> P_ki:P(w_k=1|c_i)
其中文档d可以看做|V|重独立的伯努利试验,对于给定的c_i,文档d的条件概率可以通过(3)估计这里n=|V|,同样文档d的类别可以通过公式(4)决定,把公式(6)代入(2)(4))
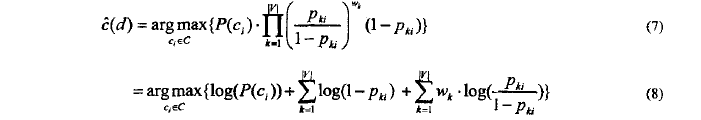
> (7)式到(8): ΠA*B=ΣlogA+ΣlogB
> (8)式中可知,虽然模型中考虑单词出现和未出现情况,但是分类起作用的实际上是w_k非零的单词。
参数估计:
模型中用到的参数都是通过训练阶段,从训练数据中学习得到的,通常取它们的最大似然估计(即(1)式中去掉分母p(d)),设训练文档集D={d1,d2,...,d|v|}
类c的概率由下式估计:
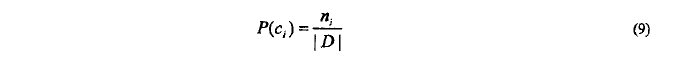
> n_i:训练集中类别c_i的 文档数
当类别c_i 的文档数为0,即n_i=0,导致p(c_i)=0.最后最大似然概率为0的后果,该如何避免?
平滑因子的出现:
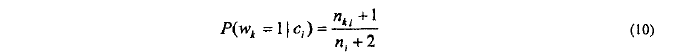
> n_i:训练集中类别c_i的 文档数
> n_ki:训练文档集中含有w_k,并且类别c_i的文档数
算法介绍与实现:
具体代码实现:
| package com.bernouli.bnc;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
import jeasy.analysis.MMAnalyzer;
public class BernouliBayesClass {
//统计某类中文档的数目
public static Map<String,Integer> classcountMap=new
HashMap<String, Integer>();
//统计训练集中总文档的数目
public static Integer datacount=0;
//训练集中所含单词通过类标进行标记(训练集的单词已经去重,不考虑频数)
public static Map<String,Integer> likelihoodMap=new
HashMap<String, Integer>();
//所有类词汇集合(总词汇表的长度)
public static Set<String> vocabularySet
= new HashSet<String>();
/**
* 建立朴素贝叶斯文本分类模型
* @param fileDirPath 文件目录
*/
public static void BayesModel (String fileDirPath){
try{
File dir=new File(fileDirPath);
if(dir.exists()&&dir.isDirectory()){
File[] files=dir.listFiles(); //获取所有训练集文件
//遍历训练集文件
for(File file:files){
String classNo=file.getName().split("\\_")[0];//获取文件类标
FileInputStream stream=new FileInputStream(file);
//获取文件流
InputStreamReader strRead=new InputStreamReader(stream,"UTF-8");
//对文件进行读取,且指定编码格式
BufferedReader bufReader = new BufferedReader(strRead);
String line=null;
//读取文件内容
while((line=bufReader.readLine())!=null){
//统计某类文档的数目
if(classcountMap.containsKey(classNo)){
classcountMap.put(classNo, classcountMap.get(classNo)+1);
}
else{
classcountMap.put(classNo, 1);//第一次存数据,没有类标,但是已经读取一行,故设置1
}
String lineText = line.trim(); //除去字符串开头和末尾的空格或其他字符
String[] words = lineText.split(" ");
Set<String> wordaSet = arrayToSet(words);//单词去重,列出词汇表的尺寸
if(!wordaSet.isEmpty()){
vocabularySet.addAll(wordaSet);//加入词汇表集合
}
//遍历所有单词
for(String word:words){
String wordNo=word+"_"+classNo;
if(likelihoodMap.containsKey(wordNo)){
likelihoodMap.put(wordNo, likelihoodMap.get(wordNo)+1);
}
else{
likelihoodMap.put(wordNo, 1);
}
}
datacount++;
}
strRead.close();
}
}
else{
System.out.println("找不到目录文件"+fileDirPath);
}
}
catch (Exception e) {
System.out.println("出错信息描述如下:"+e.getMessage());
}
}
/**
* 将数组转换成Set集合(相当于去重)
* @param words
* @return
*/
public static Set<String> arrayToSet(String[]
words){
Set<String> wordaSet = new HashSet<String>();
for (String word:words) {
if(""!=word&&!word.equals("")){
wordaSet.add(word);
}
}
return wordaSet;
}
/**
* 对字符串进行中文分词处理
* @param text 给定预处理的字符串
* @param splitToken 用于分割的标记。如","
* @return 处理后的字符串
*/
public static String SplitWords (String text,String
splitToken){
String result = null;
MMAnalyzer analyzer = new MMAnalyzer(); //极易中文分词
try{
result = analyzer.segment(text, splitToken);
}
catch (IOException e){
e.printStackTrace();
}
return result;
}
/**
* 对测试文本进行分类预测
* @param testText 测试数据集
* @return 返回分类结果
*/
public static String PredictReslut (String testText){
String PredictResult="";
testText=SplitWords(testText, " ");
// 对测试文档进行中文分词处理
String[] words=testText.split(" ");
//对字符串进行分割
Set<String> wordSet = arrayToSet(words);//单词去重,获取测试集的单词表尺寸
//TODO 不存在的单词的校验
wordSet.addAll(vocabularySet);
double argmax = Double.NEGATIVE_INFINITY;//最大类概率(默认值为负无穷小),是否可以写成0?(无穷小本身就是接近0)
//for (Iterator iterator = classcountMap.keySet().iterator();
iterator.hasNext();)
Iterator iterator= classcountMap.keySet().iterator();//遍历
while(iterator.hasNext()){
String classNo = (String) iterator.next();
double prior = classcountMap.get(classNo)/(double)datacount;//先验概率
double likelihoodProbability=0; //初始化似然概率
//根据公式求解最大似然概率,其中words相当于属性即多维的
for (String word:wordSet){
if(""!=word){
String word_classNo = word+"_"+classNo;
//获取测试数据的单词类别
//与训练数据词库进行对比,求得相似的概率
if(likelihoodMap.containsKey(word_classNo)){
//将连乘装换成对数相加【ln(a*b)=lna+lnb】,提高效率
likelihoodProbability += Math.log((likelihoodMap.get(word_classNo)+1)
/((double)classcountMap.get(classNo)+2));
}
else{
likelihoodProbability +=Math.log((1-1/(double)(classcountMap.get(classNo)+2)));
}
}
}
//利用自然对数e^loga = a,取得原始值
likelihoodProbability += Math.exp(likelihoodProbability)*prior;
System.out.println("最大似然概率:"+argmax);
System.out.println("第["+classNo+"]类似然概率:"+likelihoodProbability);
if(likelihoodProbability>argmax){
argmax = likelihoodProbability; //最大似然概率一直保持最大的似然概率
PredictResult = classNo; //返回分类的结果
}
}
System.out.println("********");
System.out.println("【伯努利模型最终分类结果:】"+PredictResult);
return PredictResult;
}
public static void main(String[] args) {
long beginTime=System.currentTimeMillis();
String filedir="./data_training";
String testText = "南京 爆炸 事件 中 , 南京 电视台
生活 频道 因为 最 早 做 了 现场 直播 而 受到 上级 批评 ; 爆出 “ 最 牛1
官腔 ” 的1 江苏 电视台 城市 频道 也 因 直播 此 事 被 上级 批评 , 相关
栏目 也 面临 停 播 。 不 知道 是 官员 的1 可悲 、 人民 的1 可悲 , 还
是 记者 的1 可悲 ! 一 个 悲剧 的1 社会 ! 真 TM 龌龊";
BayesModel(filedir);
PredictReslut(testText);
long endTime=System.currentTimeMillis();
long between=endTime-beginTime;
System.out.println("共计用时:"+between+"毫秒");
}
} |
运行结果:

4 多项式模型
概述
比BIM更为常用,与BIM不同,多项式,模型考虑单词在文档中的词频信息。最终处理还是后验条件概率在建模和预测的影响,不同于以上先验概率的求解。下面具体剖析。
分类模型
模型中,文档可以看做一个长度为f的单词序列(同一个单词可出现多次),并假设文档的长度与类别无关,而且每个单词出现的位置与其他单词独立,设单词w_k在文档中词频f_k。
文档d在给定类别c_i的条件概率p(d|c_i)可由下面公式:
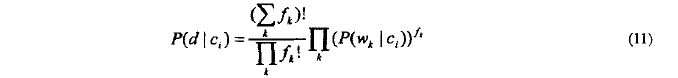
将(11)式代入(4)得多项式模型的分类判别规则:
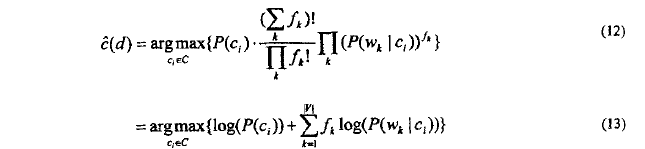
> 多项式模型在判别文档d的类别时,同样只是使用频数非零的单词。(多项式也是通过文档中出现单词来判定文档类别)
参数估计
对于类别c_i的先验概率估计。多项模型与二项模型一样,都使用公式(9)
单词w_k对于类c_i的条件先验条件概率的估计(多项式考虑同一词多次出现)
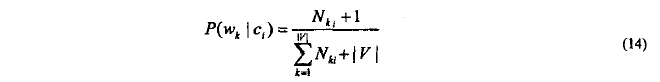
> n_ki:w_k在类别c_i中出现总次数
> |V|: 训练集中单词表的尺寸
算法介绍与实现
算法实现:
| package com.multinomial.bnc;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
import jeasy.analysis.MMAnalyzer;
public class MultinoBayesclass {
//词汇表集合(词汇表的尺寸,不考虑频数,即重复单词)
public static Set<String> vocabularySet
= new HashSet<String>();
//属于总的单词数
public static Integer datacount=0;
//训练文档中含有单词并且类标为某类的单词数
public static Map<String,Integer> likelihoodMap=new
HashMap<String, Integer>();
//训练集中某类的单词数
public static Map<String,Integer> classVocabularyMap=new
HashMap<String, Integer>();
/**
* 建立朴素贝叶斯文本分类模型
* @param fileDirPath 文件目录
*/
public static void BayesModel(String fileDirPath){
try{
File dir=new File(fileDirPath);
if(dir.exists()&&dir.isDirectory()){
File[] files=dir.listFiles(); //获取所有训练集文件
//遍历训练集文件
for(File file:files){
String classNo=file.getName().split("\\_")[0];//获取文件类标
FileInputStream stream=new FileInputStream(file);
//获取文件流
InputStreamReader strRead=new InputStreamReader(stream,"UTF-8");
//对文件进行读取,且指定编码格式
BufferedReader bufReader = new BufferedReader(strRead);
String line=null;
//读取文件内容
while((line=bufReader.readLine())!=null){
String lineText = line.trim(); //除去字符串开头和末尾的空格或其他字符
String[] words = lineText.split(" ");
//加入词汇表集合
for(String word:words){
vocabularySet.add(word);
//统计某类中的单词总数
if(classVocabularyMap.containsKey(classNo)){
classVocabularyMap.put(classNo, classVocabularyMap.get(classNo)+1);
}
else{
classVocabularyMap.put(classNo, 1);
}
//统计某类中某个单词出现的次数
String wordNo=word+"_"+classNo;
if(likelihoodMap.containsKey(wordNo)){
likelihoodMap.put(wordNo, likelihoodMap.get(wordNo)+1);
}
else{
likelihoodMap.put(wordNo, 1);
}
}
datacount++;
}
strRead.close();
}
}
else{
System.out.println("找不到目录文件"+fileDirPath);
}
}
catch (Exception e) {
System.out.println("出错信息描述如下:"+e.getMessage());
}
}
/**
* 对测试文本进行分类预测
* @param testText 测试数据集
* @return 返回分类结果
*/
public static String PredictReslut(String testText)
{
int vsSize = vocabularySet.size();//词汇表长度
String PredictResult="";
testText=SplitWords(testText, " ");//
对测试文档进行中文分词处理
String[] words=testText.split(" ");
//对字符串进行分割
double argmax = Double.NEGATIVE_INFINITY;//最大类概率(默认值为负无穷小),是否可以写成0?(无穷小本身就是接近0)
Iterator iterator= classVocabularyMap.keySet().iterator();//遍历
while(iterator.hasNext())
{
String classNo = (String) iterator.next();
double prior = classVocabularyMap.get(classNo)/(double)datacount;//先验概率
double likelihoodProbability=0; //初始化似然概率
//根据公式求解最大似然概率,其中words相当于属性即多维的
for (String word:words)
{
if(""!=word)
{
String word_classNo = word+"_"+classNo;
//获取测试数据的单词类别
//与训练数据词库进行对比,求得相似的概率
if(likelihoodMap.containsKey(word_classNo)){
//将连乘装换成对数相加【ln(a*b)=lna+lnb】,提高效率
likelihoodProbability += Math.log((likelihoodMap.get(word_classNo)+1)/ ((double)classVocabularyMap.get(classNo)+vsSize));
}
else{
likelihoodProbability += Math.log((1/(double)
(classVocabularyMap.get(classNo)+vsSize)));
}
}
}
//利用自然对数e^loga = a,取得原始值
likelihoodProbability +=Math.exp(likelihoodProbability)*prior;
System.out.println("最大似然概率:"+argmax);
System.out.println("第["+classNo+"]类似然概率:"+likelihoodProbability);
if(likelihoodProbability>argmax)
{
argmax = likelihoodProbability; //最大似然概率一直保持最大的似然概率
PredictResult = classNo; //返回分类的结果
}
}
System.out.println("****************");
System.out.println("【多项式模型最终分类结果:】"+PredictResult);
return PredictResult;
}
/**
* 对字符串进行中文分词处理
* @param text 给定预处理的字符串
* @param splitToken 用于分割的标记。如","
* @return 处理后的字符串
*/
public static String SplitWords (String text,String
splitToken){
String result = null;
MMAnalyzer analyzer = new MMAnalyzer(); //极易中文分词
try{
result = analyzer.segment(text, splitToken);
}
catch (IOException e){
e.printStackTrace();
}
return result;
}
public static void main(String[] args) {
String filedir="./data_training";
String testText = "南京 爆炸 事件 中 , 南京 电视台
生活 频道 因为 最 早 做 了 现场 直播 而 受到 上级 批评 ; 爆出 “ 最 牛1
官腔 ” 的1 江苏 电视台 城市 频道 也 因 直播 此 事 被 上级 批评 , 相关
栏目 也 面临 停 播 。 不 知道 是 官员 的1 可悲 、 人民 的1 可悲 , 还
是 记者 的1 可悲 ! 一 个 悲剧 的1 社会 ! 真 TM 龌龊";
BayesModel(filedir);
PredictReslut(testText);
}
} |
运行结果:

5 混合模型
思想概述
在估计单词对类别的先验概率时使用二项独立模型,而分类阶段估计类别对于特分类文档的后验概率时,使用多项式模型
对比体现
二项独立模型缺点:只考虑单词出现和不出现的情况,忽略了频率信息(有可能混淆了重要单词和不重要单词区别)
多项式模型缺点:假设过于严格,即假设同一单词在同一文档中的多次出现是独立的(事实并非如此)
二项独立模型假设:不同单词在同一文档中多次出现相互独立
多项式假设:同一单词在同一文档中多次出现相互独立(显然比较二项式假设更不合理)
实际中,训练文档通常充足,不使用单词在文档中的频率信息,也可以很好的分类,过多考虑频率信息非但不会对分类有帮助,反而起相反作用。但是在训练阶段可以不考虑频率信息,在分类阶段,我们针对文档,这时单词在文档中的频数信息尤为重要。如果
仅仅考虑出现与否,不同类别出现共同频数高的词被忽略,可能导致分类误差大
先验条件概率:通过m估计
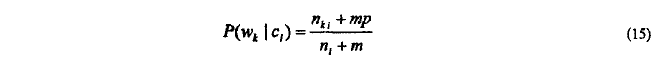
> n_ki:w_k与c_i同时出现的次数
> n_i:训练集中类别c_i的出现的次数
> p:w_k在c_i出现的估计概率
> m:等效样本数
注:二项独立模型中取p=1/2,m=2
多项式模型取p=1/|V| , m=|V| |V|:单词表尺寸
然而。实际中某类的局部单词表比整个数据集小得多,因此BIM中估计模型中单词对类条件先验概率取p=1/2不合理。故混淆模型中估计p(w_K|c_i)时,不使用公式(10),而参考MM模型中处理方式取p=1/|v|,m=|v|
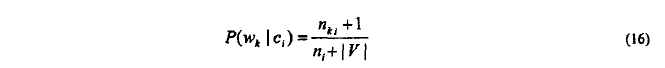
> n_ki:训练文档含有单词W_k并且为c_i的文档数
> n_i:训练文档中类别c_i的文档次数
> |V|:单词表尺寸
混淆模型的朴素贝叶斯算法
算法2:混淆模型的朴素贝叶斯分类器
训练阶段:利用公式(16)估计先验条件概率p(w_k|c_i),利用公式(9)估计概率p(c_i)。
分类阶段:给定待分类文档d用公式(13)决定它的类别。
6 综述
1. 事先收集处理数据集(涉及网络爬虫和中文切词,特征选取)
2. 预处理:(去掉停用词,移除频数过小的词汇【根据具体情况】)
3. 实验过程:
数据集分两部分(3:7):30%作为测试集,70%作为训练集
增加置信度:10-折交叉验证(整个数据集分为10等份,9份合并为训练集,余下1份作为测试集。一共运行10遍,取平均值作为分类结果)优缺点对比分析
4. 评价标准:
宏评价&微评价
新的平滑因子
引入单词量相关的平滑因子,p仍旧为1/|V|,而等效样本数m则取平均每类包含的单词量的α倍(α<<1)得到:
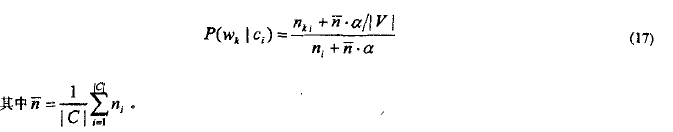
在算法2中,用公式(11)代替(16)对p(w_k|c_i)进行估计。
7 结束语
本文的对之前项目和资料进行整理总结所得,完整的写了一天,对博客园的编辑器小小抱怨,书写公式太不方便
了。抛开次要问题。本文还有待完善的部分:多个数据集分类效果的比较、不同平滑因子分类结果、分类结果的验证(比如10-折交叉验证)、与决策树支持向量机分类的优缺点比较等。在文档整理过程中不少内容没有一一写进了,包括部分内容只是提取核心知识,欢迎大家指正和优化。需要源码可以私信我。笔者接下来研究方向:
k均值、分层聚类、谱聚类的区别和聚类实现
关于主动学习的领域本体构建
机器学习算法研究 |
