| 编辑推荐: |
本文主要介绍pure pursuit 算法的方法,算法步骤,基于python的代码实现,希望对您的学习有所帮助。
本文来自于csdn,由火龙果软件Alice编辑、推荐。 |
|
0.导论
pure pursuit 方法是基于几何追踪的路径追踪方法,基于几何的控制方法较为简单和直接,不用考虑车辆的运动学模型和动力学模型,控制时使用的参数少,能够较好的运用到实践使用中。最常用的两种方法是pure
pursuit方法和stanly方法。这里主要介绍pure pursuit 方法
1.算法原理和思想
pure pursuit建立在两个模型上,阿克曼转向几何模型和二维自行车模型。
参数说明:
δ: 车辆的转向角;
L : 为车轴长度
R: 转弯半径
K:是计算出来的圆弧的曲率
ld : 预瞄距离
α: 目标点方向与当前航向的夹角;
(gx , gy ):目标点;
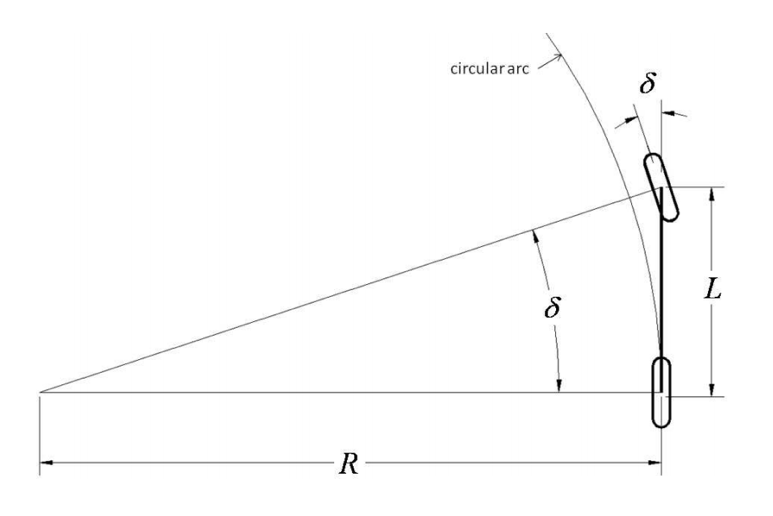
阿克曼转向模型
根据阿克曼转向几何关系,可以建立车辆前轮转向角和后轮遵循的曲率之间的关系,轮的偏向角δ,与后轮划过的圆弧的半径有以下关系:
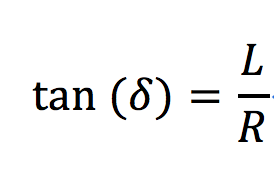
根据二维自行车模型的几何关系推导:
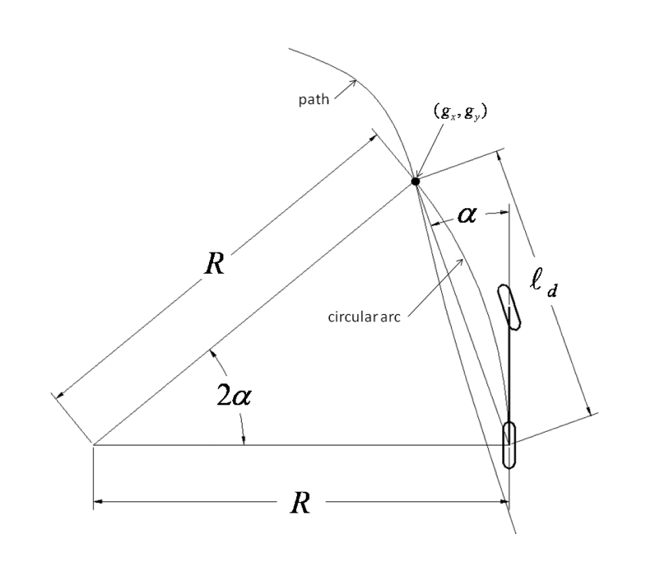
二维运动学模型

由此,建立了转向角δ与前视距离ld ,车轴长度L,目标点方向与当前航向角度α之间的关系。
pure pursuit算法的基本思想是:参考人类驾驶员的行为,以车的后轴为基点,通过控制前轮的偏向角δ,使车辆沿一条经过预瞄点的圆弧行驶。
pure pursuit算法主要参数是前视距离ld,对算法的性能影响很大。现在采取的通用方法是令前视距离ld是与速度有关的参数,不同的速度对用不同的前视距离。
2.算法步骤
查看论文《implement of the pure pursuit path tracking algorithm》,论文给出了pure
pursuit算法的的算法步骤是:
确定车辆的当前位置;
在规划出的路径中,找到离车最近的点;
找到目标点;
换算目标点坐标为车辆坐标系;
计算转向角δ并操纵车辆转向运动;
更新车辆状态
原文如下:

对各步骤的理解:
确定车辆的位置:通过gps,惯导等设备,确定车辆的位置,航向角等实时状态信息;
找到离车最近的位置:在前视距离范围内,可能会有多个数据目标路径的点,应当选取一个距离起点最接近前视距离的那个点,为了找到最满足要求的这个点,首先可以选取一个在路径上里此刻最近的点,以确定自己此刻在规划出的路径中的位置。
找到目标点:利用上一步获取的位置点,采取一定的计算方法,获取规划出的路径中,距离此点距离最接近前视距离的点,把这个点设为目标点。
利用pure pursuit算法的计算公式,计算出到达目标点所需的转向角δ。
根据单位时间内车辆的运动更新车辆的状态。
3.基于python的代码实现
参考大佬的博客,用python对代码做客复现,加入了自己对代码各个部分的思考。
这里不考虑纵向的运动控制,沿用算法中的p控制器,实验中设置为匀速运动。
首先设定参数
import numpy
as np
import math
import matplotlib.pyplot as plt
k = 0.1 # 前视距离系数
Lfc = 0.1 # 前视距离
Kp = 1.0 # 速度P控制器系数
dt = 0.1 # 时间间隔,单位:s
L = 0.6 # 车辆轴距,单位:m |
最小前视距离设置为0.1,前视距离关于车速的系数k设置为0.1 ,速度P控制器的比例系数Kp设置为1.0,时间间隔为0.1
秒,车的轴距我们定为0.6米,符合我们实验用的小车情况。
定义车辆状态类,在简单的自行车模型中,我们只考虑车辆的当前位置(x,y)(x,y),车辆的偏航角度yaw以及车辆的速度v,为了在软件上模拟,我们定义车辆的状态更新函数来模拟真实车辆的状态更新:
class VehicleState:
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw
self.v = v
def update(state, a, delta):
state.x = state.x + state.v * math.cos(state.yaw)
* dt
state.y = state.y + state.v * math.sin(state.yaw)
* dt
state.yaw = state.yaw + state.v / L * math.tan(delta)
* dt
state.v = state.v + a * dt
return state |
定义函数用于搜索最临近的路点:
这个函数主要用在pure pursuit控制器中,
def calc_target_index(state,
cx, cy):
# 搜索最临近的路点
dx = [state.x - icx for icx in cx]
dy = [state.y - icy for icy in cy]
d = [abs(math.sqrt(idx ** 2 + idy ** 2)) for (idx,
idy) in zip(dx, dy)]
ind = d.index(min(d)) # 找出最小的d所在的位置
J = 0.0
Lf = k * state.v + Lfc
'''
首先从目标点中找到一个离当前点最近的点
然后计算离这个点距离满足前视距离的下一个点
当两点之间的距离小于前视距离,需要累加几个点直至距离超过前视距离
# search look ahead target point index
# 解读:从path point 接下来中找到 离当前点最接近于 前视距离的一个点
# 当路径中的下一个点离当前很远时,这里保证了目标点至少下移一个点,不会停留在原地
'''
while Lf > J and (ind + 1) < len(cx):
dx = cx[ind + 1] - cx[ind]
dy = cy[ind + 1] - cy[ind]
J += math.sqrt(dx ** 2 + dy ** 2)
ind += 1
return ind |
定义纯追踪控制器:
def pure_pursuit_control(state,
cx, cy, pind):
ind = calc_target_index(state, cx, cy) #搜寻最近的点
ind
'''
# 每次运行 pure pursuit control时
# 首选从路径中选择一个最近的点
# 再从这个点展开,寻找一个长度为前视距离的点;
# 然后计算 转向角δ;
'''
if pind >= ind:
ind = pind
'''
# 如果初始目标点序号在搜索的点后,直接更新当前搜索点的序号为初始序号
# 在经历初次之后,把当前点赋予作为下一个目标点标志;
'''
if ind < len(cx): #若目标点没有超过范围,去具体坐标赋予 tx,ty用作目标
tx = cx[ind]
ty = cy[ind]
else: #若超过了,把最后一个点赋给目标
tx = cx[-1]
ty = cy[-1]
ind = len(cx) - 1
alpha = math.atan2(ty - state.y, tx - state.x)
- state.yaw #计算当前点到目标点的方向角差
if state.v < 0: # back
alpha = math.pi - alpha
Lf = k * state.v + Lfc #前视距离
# 前视距离的选取与速度有关,也与单位时间距离有关
delta = math.atan2(2.0 * L * math.sin(alpha) /
Lf, 1.0) #计算转向角
return delta, ind |
主函数:
与原文基本一致,修改了路径和速度,预设路径是一条螺旋线,速度设为2m/s为定值。
def main():
# 设置目标路点
cx = [0.76, 1.52, 2.28, 3.04, 3.81, 4.57, 5.33,
5.44, 5.64, 5.66, 5.33, 5.30, 4.39, 4.55, 5.33,
6.33, 6.90, 6.55, 5.33, 3.89, 3.13, 3.66, 5.33,
7.22, 8.16, 7.44, 5.33, 3.00]
cy = [0.52, 1.04, 1.57, 2.09, 2.61, 3.14, 3.66,
3.77, 3.66, 3.33, 3.03, 3.03, 3.66, 4.44, 4.92,
4.66, 3.66, 2.44, 1.78, 2.22, 3.66, 5.33, 6.18,
5.55, 3.66, 1.55, 0.52, 1.33]
target_speed = 2.0 / 3.6 # [m/s]
T = 100.0 # 最大模拟时间
# 设置车辆的出事状态
state = VehicleState(x=-0.0, y=-3.0, yaw=0.0,
v=2.0)
lastIndex = len(cx) - 1
time = 0.0
x = [state.x]
y = [state.y]
yaw = [state.yaw]
v = [state.v]
t = [0.0]
target_ind = calc_target_index(state, cx, cy)
while T >= time and lastIndex > target_ind:
ai = PControl(target_speed, state.v)
di, target_ind = pure_pursuit_control(state, cx,
cy, target_ind)
state = update(state, ai, di)
time = time + dt
x.append(state.x)
y.append(state.y)
yaw.append(state.yaw)
v.append(state.v)
t.append(time)
plt.cla()
plt.plot(cx, cy, ".r", label="course")
plt.plot(x, y, "-b", label="trajectory")
plt.plot(cx[target_ind], cy[target_ind], "go",
label="target")
plt.axis("equal")
plt.grid(True)
plt.title("Speed[km/h]:" + str(state.v
* 3.6)[:4])
plt.pause(0.001)
if __name__ == '__main__':
main() |
实验结果:红点表示事先规划好的路点,蓝线则表示我们的车辆实际运行的轨迹
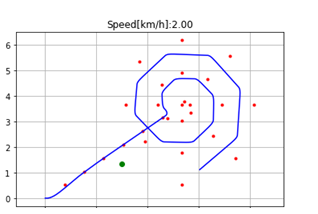
结果分析:
可以看出,pure pursuit 算法对直线追踪效果还可以。在直线路径上,一般经过1-2个点的调整,就可以很好的跟踪直线。
在曲线路径,算法的原因,车在接近目标点时,哪怕以很慢的速度,但距离只要在预瞄距离以内,小车就更新预瞄点为下一个,这样导致的情况是,小车还没到达预瞄点(距离大概在预瞄距离处时,小车便更换了预瞄点,导致对曲线路径没法做到100%的跟踪效果。
(粗略)查看了一些论文后,大致归纳了算法的改进方向(待后续补充修改):
1.在车辆运动过程中,动态地调整前视距离;
2.修改对转向角的计算方法(考虑道路曲率等因素在内,加强对曲线路径的追踪效果)。
|
