| 编辑推荐: |
本文主要以举例子的方法来讲解,运用随机森林来计算,这样可以让大家更好的理解随机森林模型,希望对您的学习有所帮助。
本文来自于csdn,由火龙果软件Alice编辑、推荐。 |
|
大家好,我是你们的好朋友小木。对于随机森林的模型,网上已经有灰常灰常多的讲解,大家讲的也非常的不错。但绝大多数大神讲解都是注重于理论,把算数的地方都给忽略了,我这次要以举例子的方法来讲解,这样可以让大家更好的理解随机森林模型。
首先我们来定义一下随机森林,啥叫随机森林呢,森林指的是有一堆大树的地方,随机指每棵大树种植的过程中施肥的种类是随机地选择的。但是好好地一个模型怎么就变成大树了呢?当然不是啦,这里大树指的是决策树,而施肥指的是不同的限定条件。接下来,又有小朋友问我啥叫决策树,好大的一棵树啊,不懂o(∩_∩)o
,那么我就来讲一下啥叫决策树。
顾名思义,决策就是评价的意思,我们用一颗大树评价一个事物,这样的大树就叫做决策树。那么我们决策啥?往后看就直到了
比如小木想要找女朋友,但他是个人,他有自己喜欢的类型,不是任何人都会同意的。我们现在有一个中介公司给小木介绍了五个女孩,她们的条件、以及小木是否想见面分别如表1所示:
表1
我们要决策的就是小木是否选择见面,其中结果有两个,一个是是,一个是否。
这个表格中有长相、性格、年龄、学历、小木是否选择几项,除了年龄之外全都是文字,我们要建立数学模型这是不可以的,那么我们必须给它们转换为数字形式,转换之后如表2所示:
表2

这个表格把各个变量都应用上了数字,例如性格中,分为了0,1,2三类。我们分完类别之后呢,下一步我们就要选择一个特征,然后判断小木是否见面。特征怎么选?我们用一个叫做熵值公式,它的计算公式如下:

举个例子,比如分析小木是否选择见面,在表格2里面,选择“是”情况有两种,“否”情况有三种,共五个,所以选择“是”的概率为2/6=0.33,选择否的概率为4/6=0.67。然后我们把0.4和0.6带入公式(1)中,得到:H0=-(0.33*log20.33+0.67*log20.67)=0.92
同理,对于学历来说,共有4种:高中、本科、硕士、博士,概率分别为:1/6、2/6、2/6、1/6,并将其带入公式2中:

其中,|Di|/|D|指的是高中、学士、硕士、博士概率。计算Hi的时候,我们带入的总数目是高中、学士、硕士、博士的数量,比如学士有两个,且一个小木不选,一个小木选,概率分别是0.5、0.5。类似于高中数学中的H(Di|Hj),要是不能理解就按照下面的计算方式直接带入数据就行:

通过式(2)可求得H4。
同理,我们得出各个特征的Hi值,然后用得出的Hi值与H0分别作差,也就是Hi-H0,然后得到如下表3:

我们把这些都算完了,就差年龄了,年龄这个条件我们却发现了,每一个年龄的概率是1/6,我们应该这么算?不,为啥呢,因为我们这里没有29岁,也没有21,22,23岁,我们要一个个算的话,那么就漏掉这四个年龄了,那怎么办?我们只好坐在轮椅上,双脚离地想想了,我们这么一想,唉,发现一个秘密。如果你说是,年龄在20~30之间,那么我就告诉你:恭喜你回答正确!因为在20~30之间,我们取一个中间值25,如果小于25我们就算0,如果大于等于25就算1,那么我们就得出了表4:
表4
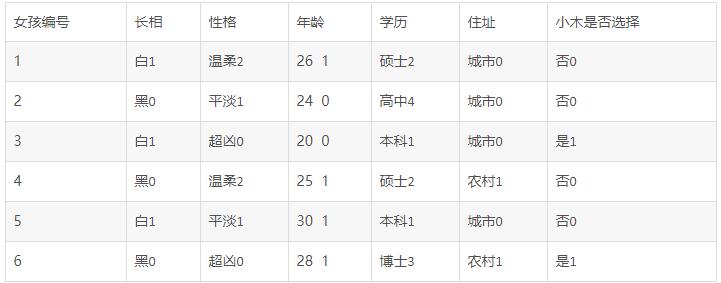
我们这里大于等于25的一共有4个,小于的一共有2个,那么它们的概率分别为4/6、2/6,通过式1计算,就能得出H=0.92,因此,我们获得完整的表5:
表5

熵值代表着混乱的程度,我们高中学过,熵值越大,说明越混乱。熵差代表着啥呢,代表着信息增益,也可以叫做纯度,说白了与小木找对象的不确定度是0.92,如果就看性格,不确定度是0,增益最大,也就是说看完性格之后就就知道怎么挑了,说明分类的纯度大,如果就看长相,不确定度增益小,也就是不挑长相,所以对找对象用途很不大,说明纯度小。总结来说是信息增益越大,挑的越容易。因为长相增益为0,那么我们就把它排除在外,不算它了。
我们建立第一颗决策树,首先随机地选择两个限定条件,一个是性格,另外一个是年龄,我们发现增益最大的是性格,也就是性格作为决策树的顶点,然后随机选择几个样本(由于样本就6个,我们就都选择了)并按照这性格分别划分三个细节,如图1所示:

图1
图1中,文字底下的数字表示的和表4中的相同,例如平淡中[1,0]表示:[平淡,小木不选择]。其中最后一位红字表示小木的选择,从图中我们可以看出,小木对于温柔、平淡的女生是拒绝的,对超凶的女生是直接选择的。对超凶的女生,小木是百分百选择的。因此后边的学历我们也就不用看了。这样一颗决策树就建立完成了。
接下来,按照同样方法再随机地选择两个限定条件,如学历、年龄。信息增益最大的那个是学历,也就是学历作为决策树的顶点,然后随机选择几个样本(由于样本就6个,我们就都选择了),按照这性格分别划分四个细节:高中、本科、硕士、博士如图2所示:

我们发现高中和硕士小木不选,而博士小木选择,本科有歧义,我们还需要往下面再分类。我们按照同样的方法,把年龄分为25岁以下和25岁以上(包含25岁),图3所示:

图3
我们再生成一个大树,选择住址和性格(因为样本太少了,所以我们这里瞎编一个大树,不符合计算规则,不用多想了),如图4所示:

图4
这样,我们建立了三颗决策树,接下来,我们需要把测试数据带入进去判断小木是否选择,比如我们有表6:
表6

然后我们把条件分别带入三棵树中。比如第一个女孩带入第一颗大树,首先判断性格,性格是平淡的,小木不会选择,所以结果为0。第二棵树,首先判断学历是高中,小木不会选择所以结果为0。带入第三棵树,判断居住地是城市,接下来判断性格为平淡,所以小木不选,结果为0。其它数据同理计算,我们会得出表格7:
表7

从表格我们可以得出最终的结果,最终的结果一般是两种计算方法,第一种是少数服从多数,第二种是平均值,因为这次结果只有0和1,所以选择少数服从多数的计算方式。
至此我们的随机森林就计算完成啦。最后总结一下随机森林的计算步骤:
(1)导入数据,条件及其结果(比如女孩自身条件是条件,小木是否选择见面是结果)
(2)设定一个常数N,作为筛选的样本数目(一般小于样本总数M,由于该举例里面样本太少了,所以我就让N=M了)。
(3)设定一个常数a,作为筛选条件的数目(一般小于总数)
(4)设定一个常数X,作为决策树数目,并创建X个决策树(创建时,每个决策树随机选定数目为a的条件,随即选定数目为N的样本)
(5)创建完成后,带入测试样本,以结果少数服从多数或平均值作为最终测试结果,并与真实结果做对比,判断是否符合实际。
|
